认识GLPK

  • GLPK是一个解决线性规划问题的工具。是GNU计划下一个用于解线性规 划(Linear Programming)的工具包。它可以方便的描述线性规划问题，并给出相应解。 因此在linux系统下安装只需 sudo apt-get install glpk一条命令即可。

win10下安装GLPK

  • 想要将glpk安装在windows系统下需要经过一些简单的配置
  • 首先便是先到官网下载glpk 地址点这里
  • 选择一个合适的版本下载（这里选择的是4.57的版本），将glpk解压到D盘（或其他盘）。
  • 打开glpk文件，由于我的电脑是64位的，所以进入往win64
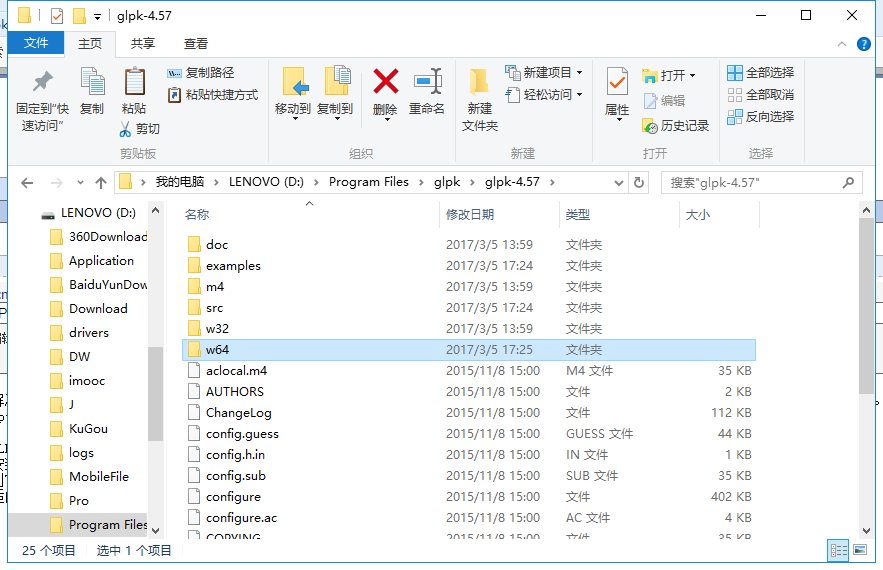
  • 仔细阅读内含的文档readme.txt，选择与自己安装的VS版本相对应的文件，修改home值（ 此处的home值应为自己的vs安装目录下VC目录的路径）
  • 由于我安装的VS版本是2015的，因此选择下图两个文件进行修改。

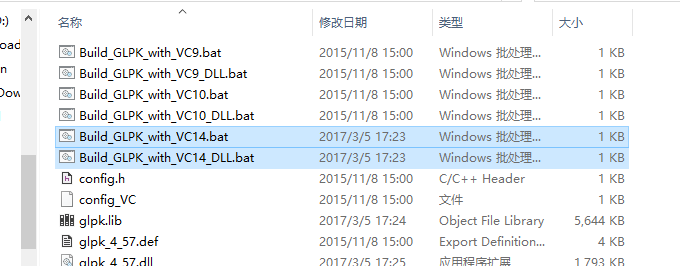
  • 单击Build_GLPK_with_VC14.bat和Build_GLPK_with_VC14_DLL.bat这两个文件，选择编辑，进行home值的修改

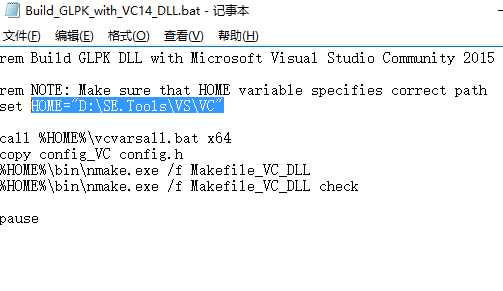
  • 完成home值修改之后，先后双击Build_GLPK_with_VC14.bat和Build_GLPK_with_VC14_DLL.bat这两个文件
  • 运行后观察是否出现OPTIMAL SOLUTION FOUND字样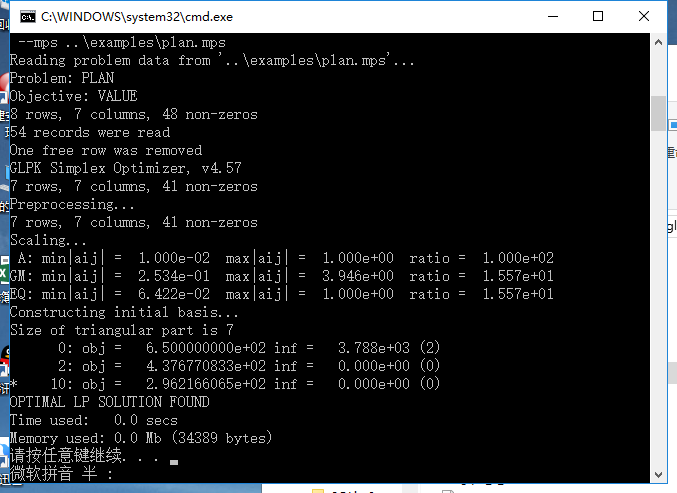

  • 到这里就基本安装成功了，可以通过看目录中是否包含以下两个文件验证。

win10下安装GLPK的更多相关文章

  1. win10下安装Ubuntu + 修复Ubuntu引导

    如何在已安装 Windows 10 的情况下安装 Linux(Ubuntu 15.04)双系统? - Microsoft Windows - 知乎http://www.zhihu.com/questi ...

  2. DELPHI7在WIN8和WIN10下安装和运行

    DELPHI7在WIN8下安装后可以打开运行,但发现设置断点DEBUG运行DLL工程时会卡死(IDE长时间无反应,不报错). DELPHI7在WIN10下安装后打开的时候会报错,无法运行. 以上两种情 ...

  3. win10下安装ubuntu18.04

    在win10下安装Ubuntu18.04,双系统共存.Ubuntu 18.04 使用的是Gnome桌面. 查看系统的启动模式: Win+R打开运行,输入msinfo32,回车查看系统信息.在BIOS模 ...

  4. vs2017 在win10下安装后开始运行asp.net core 项目时出错

    vs2017 在win10下安装后开始运行asp.net core 项目时出错 报找不到什么 解决方法: 下载 asp.net 2.2 安装好,重新启动电脑问题解决.

  5. win10下安装vs2013无法安装解决方案

    win10下安装vs2013无法安装解决方案 win+r,输入cmd进入命令行 进入界面后选择修复 进入vs_ultimate文件所在目录,输入: vs_ultimate /Uninstall    ...

  6. Win10下安装MySQL5.6

    Win10下安装MySQL5.6 我分了两种下载安装的方式给大家看,注意数据库这个东西不在乎版本是不是最新,在乎的是够稳定,现在公司中常用的是mysql5.5和mysql5.6的版本,我现在就用mys ...

  7. 在win10下安装双系统ubuntu16.04.3教程

    闲暇了两天,终于想起来要装一个Liunx系统了.于是捣鼓了一番,实现了在Win10下安装Ubuntu16.04.3版本. 一.准备工作 下载Ubuntu 16.04.3镜像 准备一个2G以上的U盘 下 ...

  8. 【暂时解决】win10下安装VS2017 15.3版本 提示 未能安装包“Microsoft.NET.4.6.FullRedist.NonThreshold.Resources,version=4.6.81.9,language=zh-CN”。

    win10下安装VS2017 15.3版本的时候,出现以上错误日志提示,请问如何解决的哇? 这个问题,开始我以为是我的安装包所在的路径问题引起的,但是我将安装包移动到了磁盘根目录进行安装,依然出现这个 ...

  9. Win10下安装zookeeper

    Win10下安装zookeeper 注册中心zookeeper的安装 0.去Apache官网下载zookeeper http://zookeeper.apache.org/ 2.找到解压路径的conf ...

随机推荐

  1. i.s.h.med Enhancement for cancelling an appointment

    This article intends to introduce my experience about enhancement for canceling an appointment. I tr ...

  2. postMessage 实现跨源通信 iframe 跨域获取url

    用postMessage实现跨源通信的方法实例 如:在www.bbb.com/index.html页面获取www.aaa.com/index.html的数据,以iframe的形式 www.aaa.co ...

  3. vue实例详解

    Vue实例的构造函数 每个 Vue.js 应用都是通过构造函数 Vue 创建一个 Vue 的根实例 启动的 虽然没有完全遵循 MVVM 模式, Vue 的设计无疑受到了它的启发.因此在文档中经常会使用 ...

  4. Android事件处理第一节（View对Touch事件的处理）

    http://ipjmc.iteye.com/blog/1694146 在Android里Touch是很常用的事件,尤其实在自定义控件中,要实现一些动态的效果,往往要对Touch进行处理.Androi ...

  5. OPENSTACK在RHEL7安装；admin创建虚拟机模板供demo使用

    版权声明:本文为博主原创文章,未经博主同意不得转载. https://blog.csdn.net/u010026901/article/details/30965601 首先RHEL7安装.导入镜像, ...

  6. java开发过程问题及解决

    1.junit做测试时候报异常: junit.framework.AssertionFailedError: No tests found in com.mq.original.OriginalMqP ...

  7. 浅淡个人学习嵌入式Linux过程

    我专业是电子信息工程,在初入大学的时候,我们的班主任便要我们多多去了解一些关于电子方面的知识.后来我了解到了嵌入式,继而了解到了嵌入式Linux.其实我们学习linux差不多就学习linux内核,但是 ...

  8. mysql5.6.8源码安装

    内核: [root@opop ~]# cat /etc/centos-release CentOS release 6.8 (Final)[root@opop ~]# uname -aLinux op ...

  9. Canvas绘图优化之使用位图--基于createjs库

    在地图上实时绘制大量(万级别)图形,实时绘制的原因是因为各个图形形状不同,图形要按照后端传送的参数来绘制. 用canvas绘制图形比较方便,javascript的api接口也比较简单.现在也有很多的j ...

  10. WebForms UnobtrusiveValidationMode requires a ScriptResourceMapping for 'jquery'. Please add a ScriptResourceMapping named jquery(case-sensitive).

    新开一个Web site.没有使用jQuery,当Insus.NET使用一些验证控件时,如RequiredfieldValidator,程序出现下面错误: WebForms UnobtrusiveVa ...