贝叶斯---最大似然估计（高翔slam---第六讲 ）

1.贝叶斯---最大似然估计

回顾一下第二讲的经典SLAM模型：

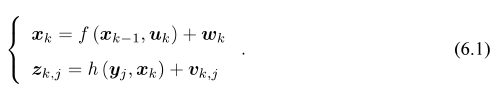
通过传感器（例如IMU）的运动参数u来估计运动(位姿x)[定位]，通过相机的照片的观测参数z来估计物体的位置(地图y)[建图]，都是有噪声的。因为运动参数和照片都有噪声，所以需要进行优化。而过去卡尔曼滤波只关心当前的状态估计，而非线性优化则对所有时刻采集的数据进行状态估计，被认为优于卡尔曼滤波。由于要估计所有的采集数据，所以待估计变量就变成：x={x1,…,xN,y1,….,yM}

所以对机器人状态的估计，就是求已知输入数据u(传感器参数)和观测数据z(图像像素)的条件下，计算状态x的条件概率分布（也就是根据u和z的数据事件好坏来估计x的优劣事件概率情况，这其中包含着关联，就好像已知一箱子里面有u和z个劣质的商品，求取出x个全是好商品的概率，同样的样本点，但是从不同角度分析可以得出不同的事件，不同的事件概率之间可以通过某些已知数据得出另些事件的概率）：P(x|z, u)。当没有测量运动的传感器，只考虑观测照片z的情况下求x（这个过程也称SfM运动恢复），那么就变成P(x|z)。

贝叶斯公式求解（贝叶斯法则的分母部分与带估计的状态x无关，所以忽略P(z)）：

2.最大似然估计---最小二乘问题

如何求最大似然估计呢？

回顾观测方程，我们知道z与x之间存在一个函数式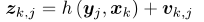：，现在要求x导致z出现的概率最大，求x。

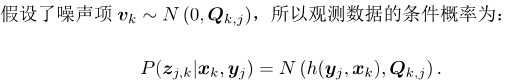
假设噪声项符号高斯分布，观测Z也符合高斯分布。

为了计算使它最大化的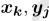，往往使用最小化负对数的方式，来求一个高斯分布的最大似然。

任意的高位高斯分布，概率密度函数展开式：

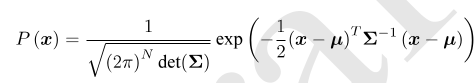
对其取负对数：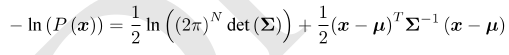

对原分布求最大化相当于对负对数求最小化，对上式x进行最小化时，第一项与x无关，略去，只需要最小化右侧的二次型，带入SLAM的观测模型，即求：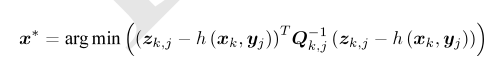

我们发现，该是等价于最小化噪声项（即误差）的平方（范数意义下）。

因此对于所以对于所有的运动和观测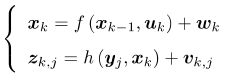，定义数据与估计值之间的误差：，

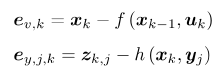误差的平方和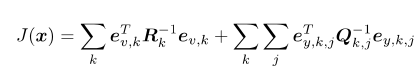：    （6.12）

从而得到了一个总体意义下的最小二乘问题，它的最优解等于状态的最大似然估计。

直观上讲，由于噪声的存在，当我们把估计的轨迹和地图(xk,yj)代入SLAM的运动、观测方程中时，它们并不会完美的成立。这时候怎么办呢？我们把状态的估计值进行微调，使得整体的误差下降一些，它一般会到极小值。这就是一个典型的非线性优化过程。