排序系列 之 希尔排序算法 —— Java实现

　基本思想：

　　希尔排序的实质就是分组插入排序，又称缩小增量法。

　　将整个无序序列分割成若干个子序列（由相隔某个“增量”的元素组成的）分别进行直接插入排序，然后依次缩减增量再进行排序，待整个序列中的元素基本有序时，再对全体元素进行一次直接插入排序。

　　因为直接插入排序在元素基本有序的情况下，效率是很高的，因此希尔排序在时间效率上有很大提高。

　实例：

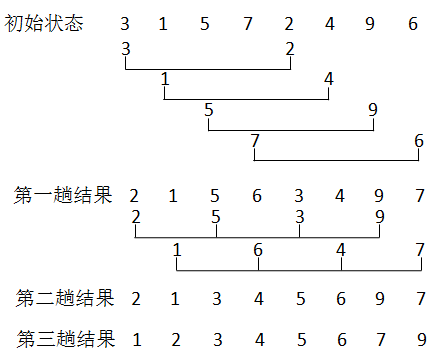
　　无序序列：int a[] = {3,1,5,7,2,4,9,6};

　　第一趟时： n=8; gap=n/2=4; 把整个序列共分成了4个子序列{3，2}、{1，4}、{5，9}、{7，6}

　　第二趟时：gap=gap/2=2; 把整个序列共分成了2个子序列{2，5，3，9}、{1，6，4，7}

　　第三趟时：对整个序列进行直接插入排序

　　

　　希尔排序是不稳定的

　Java实现：

package sort;
/**
 * 希尔排序 算法 的实现
 * @author 那一季的银杏叶
 *
 */
public class ShellSort {

    public static void main(String[] args) {
        // TODO Auto-generated method stub
        new ShellSort().run();
    }

    private void run() {
        // TODO Auto-generated method stub
        int a[] = {3,1,5,7,2,4,9,6};
        System.out.println("———————————————————希尔排序算法—————————————————————");
//        shellSort(a);
        shellSort2(a);
        printResult(a,a.length);
    }
    /**
     * 希尔排序(缩小增量法) 属于插入类排序
     * 不稳定
     * @param a
     */
    private void shellSort(int[] a){
        int n=a.length;
        int gap=n/2;
        while(gap>=1){
            for(int i=gap;i<a.length;i++){
                int j=0;
                int temp = a[i];
                for(j=i-gap;j>=0 && temp<a[j];j=j-gap){
                    a[j+gap] = a[j];
                }
                a[j+gap] = temp;
            }
            printResult(a,a.length);
            gap = gap/2;
        }
    }
    /**
     * 严格按照定义来写的希尔排序
     * @param a
     */
    private void shellSort2(int[] a){
        int n=a.length;
        int i,j,k,gap;
        for(gap=n/2;gap>0;gap/=2){
            for(i=0;i<gap;i++){
                for(j=i+gap;j<n;j+=gap){
                    int temp = a[j];
                    for(k=j-gap;k>=0 && a[k]>temp;k-=gap){
                        a[k+gap]=a[k];
                    }
                    a[k+gap]=temp;
                }
            }
            printResult(a,a.length);
        }
    }
    private void printResult(int[] a, int n){
        for(int j=0;j<n;j++){
            System.out.print(" "+a[j]);
        }
        System.out.println();
    }
}

　运行结果展示：

　　（本文仅供学习交流，如有更好的思路，欢迎留下意见供大家探讨学习~）