[NOI2002]贪吃的九头龙（树形dp）

[NOI2002]贪吃的九头龙

题目背景

传说中的九头龙是一种特别贪吃的动物。虽然名字叫“九头龙”，但这只是 说它出生的时候有九个头，而在成长的过程中，它有时会长出很多的新头，头的 总数会远大于九，当然也会有旧头因衰老而自己脱落。

题目描述

有一天，有 M 个脑袋的九头龙看到一棵长有 N 个果子的果树，喜出望外， 恨不得一口把它全部吃掉。可是必须照顾到每个头，因此它需要把 N 个果子分成 M 组，每组至少有一个果子，让每个头吃一组。

这M个脑袋中有一个最大，称为“大头”，是众头之首，它要吃掉恰好 K 个 果子 ，而 且 K 个果子中理所当然地应该包括唯一的一个 最大的果子。 果子由 N-1 根树枝连接起来，由于果树是一个整体，因此可以从任意一个果子出发沿着树枝 “走到”任何一个其他的果子。

对于每段树枝，如果它所连接的两个果子需要由不同的头来吃掉，那么两个 头会共同把树枝弄断而把果子分开；如果这两个果子是由同一个头来吃掉，那么 这个头会懒得把它弄断而直接把果子连同树枝一起吃掉。当然，吃树枝并不是很舒服的，因此每段树枝都有一个吃下去的“难受值”，而九头龙的难受值就是所 有头吃掉的树枝的“难受值”之和。

九头龙希望它的“难受值”尽量小，你能帮它算算吗？

例如图 1 所示的例子中，果树包含 8 个果子，7 段树枝，各段树枝的“难受 值”标记在了树枝的旁边。九头龙有两个脑袋，大头需要吃掉 4 个果子，其中必 须包含最大的果子。即 N=8，M=2，K=4：

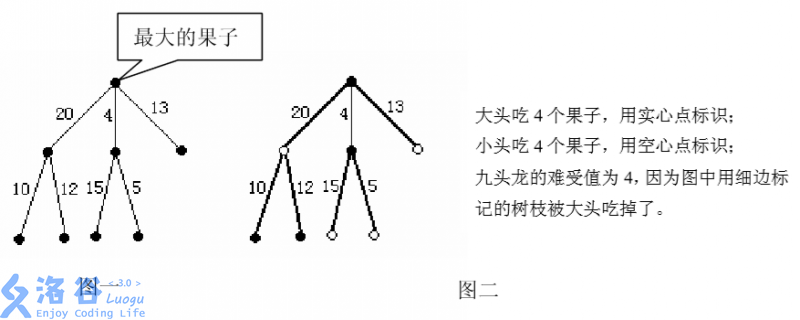
图一描述了果树的形态，图二描述了最优策略。

输入输出格式

输入格式：

输入文件 dragon.in 的第 1 行包含三个整数 N (1<=N<=300)，M (2<=M<=N)， K (1<=K<=N)。 N个果子依次编号 1,2,...,N，且 最大 的果子的 编 号 总 是 1。第 2 行到第 N 行描述了果树的形态，每行包含三个整数 a (1<=a<=N)，b (1<=b<=N)， c (0<=c<=10^5105)，表示存在一段难受值为 c 的树枝连接果子 a 和果子 b。

输出格式：

输出文件 dragon.out 仅有一行，包含一个整数，表示在满足“大头”的要求 的前提下，九头龙的难受值的最小值。如果无法满足要求，输出-1。

输入输出样例

输入样例#1： 复制

8 2 4

1 2 20

1 3 4

1 4 13

2 5 10

2 6 12

3 7 15

3 8 5

输出样例#1： 复制

4

说明

该样例对应于题目描述中的例子。

题解

一眼树形dp。

首先按照套路想了一下

\(dp[i][j][k]\)表示第\(i\)个节点，给第\(j\)个头，第\(j\)个头已有\(k\)个果子。

然而我们并不能确定第\(j\)个头的果子在哪里。

不好记录一条边连接的两端归哪个头。

且空间会炸起飞。

那么我们换一种套路。

\(f[i][j]\)表示第\(i\)个节点选\(j\)个给\(1\)号头。

但是其他头会对题目有影响啊。

可以说样例给的很套路了。

我给个\(m==2\)，说明不给大头就给小头。

没得选择。

但实际上，如果有多个小头。就一定不会吃树枝。

因为当前点吃了是2号头。那么那个点的儿子让3号吃就可以了。

再往下的一层给2号。以此交替。

所以我们就可以用\(f[i][j][0/1]\)表示\(1\)号头取不取了。

因为其他的节点的贡献就在于\(m==2\)？边权:0。

那么转移为

for(int j=0;j<=k;j++)
{
	for(int t=0;t<=j;t++){
	f[x][j][0]=min(f[x][j][0],min(dp[j-t][0]+f[v][t][1],dp[j-t][0]+f[v][t][0]+(m==2)*e[i].v));
	f[x][j][1]=min(f[x][j][1],min(dp[j-t][1]+f[v][t][0],dp[j-t][1]+f[v][t][1]+e[i].v));
	}
}
//注意这里的f数组不会及时更新。要用dp数组先代替。因为f越来越小对后面的选择会有后效性。

代码

#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<iostream>
using namespace std;
const int N=305;
int n,m,k,f[N][N][2],dp[N][2];
struct node{
    int to,nex,v;
}e[N<<1];
int num,head[N];
int read(){
    int x=0,w=1;char ch=getchar();
    while(ch>'9'||ch<'0'){if(ch=='-')w=-1;ch=getchar();}
    while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();
    return x*w;
}

void add(int from,int to,int v){
    num++;
    e[num].to=to;
    e[num].v=v;
    e[num].nex=head[from];
    head[from]=num;
}

void dfs(int x,int fa){
    f[x][1][1]=f[x][0][0]=0;
    for(int i=head[x];i;i=e[i].nex){
        int v=e[i].to;if(v==fa)continue;
        dfs(v,x);
        for(int j=0;j<=k;j++){
            dp[j][0]=f[x][j][0];
            dp[j][1]=f[x][j][1];
        }
        memset(f[x],63,sizeof(f[x]));
        for(int j=0;j<=k;j++){
            for(int t=0;t<=j;t++){
                f[x][j][0]=min(f[x][j][0],min(dp[j-t][0]+f[v][t][1],dp[j-t][0]+f[v][t][0]+(m==2)*e[i].v));
                f[x][j][1]=min(f[x][j][1],min(dp[j-t][1]+f[v][t][0],dp[j-t][1]+f[v][t][1]+e[i].v));
            }
        }
    }
}

int main(){
    n=read();m=read();k=read();
    if(m-1>n-k){printf("-1");return 0;}
    for(int i=1;i<n;i++){
        int x=read(),y=read(),z=read();
        add(x,y,z);add(y,x,z);
    }
    memset(f,63,sizeof(f));
    dfs(1,0);
    printf("%d\n",f[1][k][1]);
    return 0;
}