自编码器----Autoencoder

一、自编码器：降维【无监督学习】

PCA简介：【线性】原矩阵乘以过渡矩阵W得到新的矩阵，原矩阵和新矩阵是同样的东西，只是通过W换基。

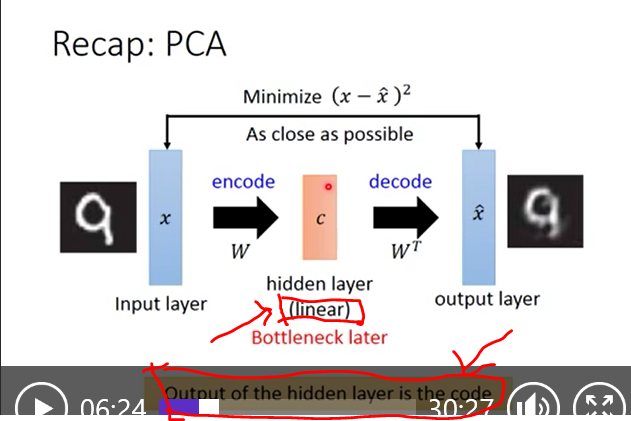
自编码：

自动编码器是一种无监督的神经网络模型，它可以学习到输入数据的隐含特征，这称为编码(coding)，同时用学习到的新特征可以重构出原始输入数据，称之为解码(decoding)。从直观上来看，自动编码器可以用于特征降维，类似主成分分析PCA，但是其相比PCA其性能更强，这是由于神经网络模型可以提取更有效的新特征。除了进行特征降维，自动编码器学习到的新特征可以送入有监督学习模型中，所以自动编码器可以起到特征提取器的作用。作为无监督学习模型，自动编码器还可以用于生成与训练样本不同的新数据，这样自动编码器（变分自动编码器，VariationalAutoencoders）就是生成式模型。

类型：堆栈自动编码器(StackedAutoencoder)、去噪自动编码器(DenoisingAutoencoder)，稀疏自动编码器(SparseAutoencoder)以及变分自动编码器。

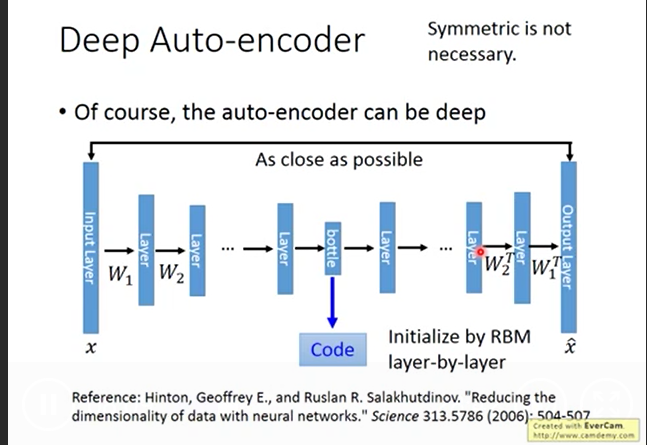
自编码和PCA的区别：

由于神经网络能够学习非线性关系，因此可以认为这是PCA更有力（非线性）的泛化。而PCA试图发现描述原始数据的低维超平面，自编码器则能够学习非线性流形（流形为连续的非交叉的曲面）。这两种方法之间的区别如下图所示。

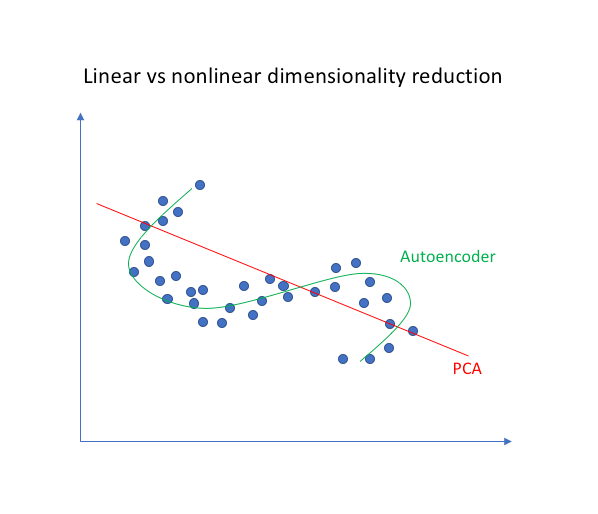
自编码还原的结果比PCA清晰。

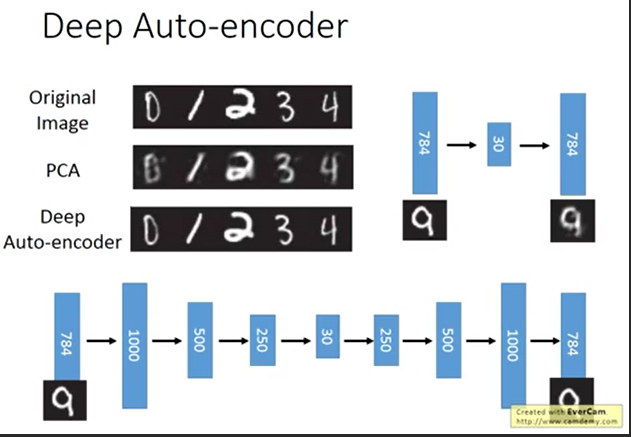
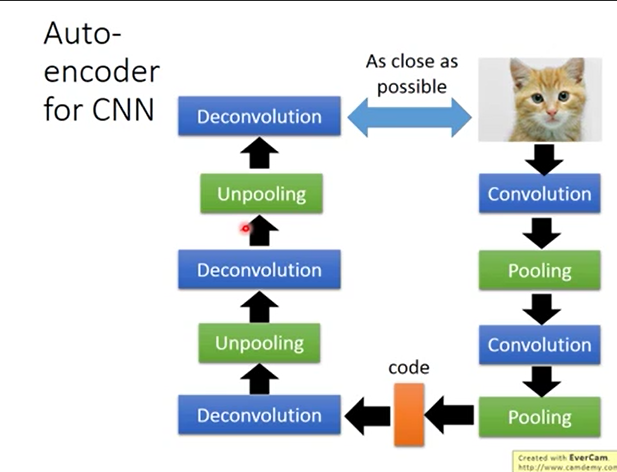
而两者的重点是要拿到比较好的30维code。

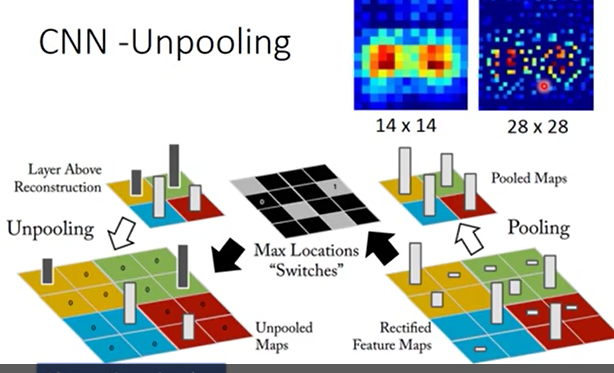
二、降噪自编码【加噪声】

三、CNN、DNN、RBM、DBN来实现自编码：