sklearn学习9----LDA（discriminat_analysis）

1、导入模块

http://scikit-learn.org/stable/modules/generated/sklearn.discriminant_analysis.LinearDiscriminantAnalysis.html#sklearn.discriminant_analysis.LinearDiscriminantAnalysis

from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
da = LinearDiscriminantAnalysis()

---

2、使用参数说明：https://blog.csdn.net/qsczse943062710/article/details/75977118

class sklearn.discriminant_analysis.LinearDiscriminantAnalysis(solver=’svd’, shrinkage=None, priors=None, n_components=None, store_covariance=False, tol=0.0001)

• solver：str，求解算法，
  取值可以为：
  • svd：使用奇异值分解求解，不用计算协方差矩阵，适用于特征数量很大的情形，无法使用参数收缩（shrinkage）
  • lsqr：最小平方QR分解，可以结合shrinkage使用
  • eigen：特征值分解，可以结合shrinkage使用
• shrinkage：str or float，是否使用参数收缩
  取值可以为：
  • None：不适用参数收缩
  • auto：str，使用Ledoit-Wolf lemma
  • 浮点数：自定义收缩比例
• priors：array，用于LDA中贝叶斯规则的先验概率，当为None时，每个类priors为该类样本占总样本的比例；当为自定义值时，如果概率之和不为1，会按照自定义值进行归一化
• n_components：int，需要保留的特征个数，小于等于n-1
• store_covariance：是否计算每个类的协方差矩阵

---

3、方法：

---

4、LinearDiscriminantAnalysis类的fit方法

 def fit(self, X, y, store_covariance=None, tol=None):
    类型检查，包括priors的检测
    根据不同的solver调用不同的求解方法 

• 1
• 2
• 3

  fit()方法里根据不同的solver调用的方法均为LinearDiscriminantAnalysis的类方法

fit()返回值：

• self：LinearDiscriminantAnalysis实例对象

属性：

• covariances_：每个类的协方差矩阵， shape = [n_features, n_features]
• means_：类均值，shape = [n_classes, n_features]
• priors_：归一化的先验概率
• rotations_：LDA分析得到的主轴，shape [n_features, n_component]
• scalings_：数组列表，每个高斯分布的方差σ

---

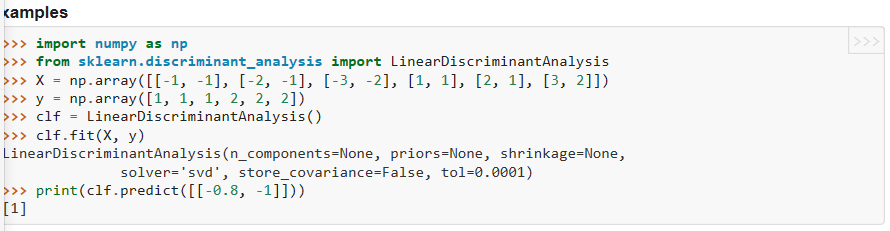
5、使用例子(可预测、可降维）

from sklearn.discriminat_analysis import LinearDiscriminantAnalysis as LDA

sklearn_lda=LDA(n_components=2)
X_lda_sklearn=sklearn_lda.fit_transform(X,Y)