平衡二叉树的插入过程:http://www.cnblogs.com/hujunzheng/p/4665451.html

对于二叉平衡树的删除采用的是二叉排序树删除的思路:

　　假设被删结点是*p，其双亲是*f，不失一般性，设*p是*f的左孩子，下面分三种情况讨论：
　　⑴ 若结点*p是叶子结点，则只需修改其双亲结点*f的指针即可。
　　⑵ 若结点*p只有左子树PL或者只有右子树PR，则只要使PL或PR 成为其双亲结点的左子树即可。
　　⑶ 若结点*p的左、右子树均非空，先找到*p的中序前趋结点*s（注意*s是*p的左子树中的最右下的结点，它的右链域为空），然后有两种做法：
　　　　① 令*p的左子树直接链到*p的双亲结点*f的左链上,而*p的右子树链到*p的中序前趋结点*s的右链上。
　　　　② 以*p的中序前趋结点*s代替*p（即把*s的数据复制到*p中），将*s的左子树链到*s的双亲结点*q的左（或右）链上。

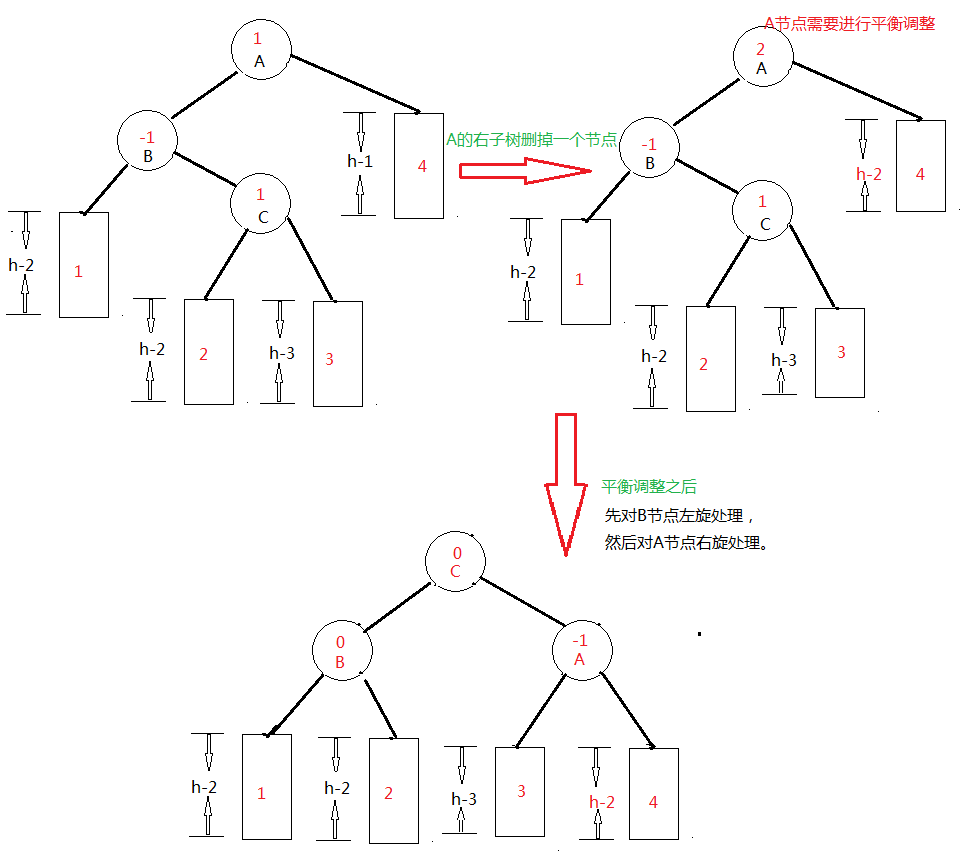
注：leftBalance_del 和 rightBalance_del方法是在删除节点时对左子树和右子树的平衡调整，leftBalance 和 rightBalance方法是在插入节点是对左右子树的平衡调整。 在具体调整的时候，和插入式调整时运用同样的分类方法，这里介绍一种情况，如下图所示（代码部分见代码中的提示）

  1. #include<iostream>
  2. #include<cstring>
  3. #include<string>
  4. #include<queue>
  5. #include<map>
  6. #include<cstdio>
  7. #define LH 1 //左高
  8. #define EH 0 //等高
  9. #define RH -1 //右高
  10. using namespace std;
  11.  
  12. template <typename ElemType>
  13. class BSTNode{
  14.     public:
  15.         ElemType data;//节点的数据
  16.         int bf;//节点的平衡因子
  17.         BSTNode *child[];
  18.         BSTNode(){
  19.             child[] = NULL;
  20.             child[] = NULL;
  21.         }
  22. };
  23.  
  24. typedef BSTNode<string> BSTnode, *BSTree;
  25.  
  26. template <typename ElemType>
  27. class AVL{
  28.     public:
  29.         BSTNode<ElemType> *T;
  30.         void buildT();
  31.         void outT(BSTNode<ElemType> *T);
  32.         void deleteAVL(BSTNode<ElemType>* &T, ElemType key, bool &shorter);
  33.         bool insertAVL(BSTNode<ElemType>* &T, ElemType key, bool &taller);
  34.     private:
  35.         void deleteNode(BSTNode<ElemType>* T, BSTNode<ElemType>* &s, BSTNode<ElemType>* p, bool flag, bool &shorter);
  36.         void rotateT(BSTNode<ElemType>* &o, int x);//子树的左旋或者右旋
  37.         void leftBalance(BSTNode<ElemType>* &o);
  38.         void rightBalance(BSTNode<ElemType>* &o);
  39.  
  40.         void leftBalance_del(BSTNode<ElemType>* &o);
  41.         void rightBalance_del(BSTNode<ElemType>* &o);
  42. };
  43.  
  44. template <typename ElemType>
  45. void AVL<ElemType>::rotateT(BSTNode<ElemType>* &o, int x){
  46.     BSTNode<ElemType>* k = o->child[x^];
  47.     o->child[x^] = k->child[x];
  48.     k->child[x] = o;
  49.     o = k;
  50. }
  51.  
  52. template <typename ElemType>
  53. void AVL<ElemType>::outT(BSTNode<ElemType> *T){
  54.     if(!T) return;
  55.     cout<<T->data<<" ";
  56.     outT(T->child[]);
  57.     outT(T->child[]);
  58. }
  59.  
  60. template <typename ElemType>
  61. void AVL<ElemType>::buildT(){
  62.    T = NULL;
  63.    ElemType key;
  64.    while(cin>>key){
  65.            if(key==) break;
  66.            bool taller = false;
  67.            insertAVL(T, key, taller);
  68.    }
  69. }
  70.  
  71. template <typename ElemType>
  72. void AVL<ElemType>::deleteNode(BSTNode<ElemType>* T, BSTNode<ElemType>* &s, BSTNode<ElemType>* p, bool flag, bool &shorter){
  73.     if(flag){
  74.         flag = false;
  75.         deleteNode(T, s->child[], s, flag, shorter);
  76.         if(shorter){
  77.             switch(s->bf){
  78.                 case LH:
  79.                     s->bf = EH;
  80.                     shorter = false;
  81.                     break;
  82.                 case EH:
  83.                     s->bf = RH;
  84.                     shorter = true;
  85.                     break;
  86.                 case RH:
  87.                     rightBalance_del(s);
  88.                     shorter = false;
  89.                     break;
  90.             }
  91.         }
  92.     } else {
  93.         if(s->child[]==NULL){
  94.             T->data = s->data;
  95.             BSTNode<ElemType>* ss = s;
  96.             if(p != T){
  97.                 p->child[] = s->child[];
  98.             } else {
  99.                 p->child[] = s->child[];
  100.             }
  101.             delete ss;//s是引用类型，不能delete s
  102.             shorter = true;
  103.             return ;
  104.         }
  105.         deleteNode(T, s->child[], s, flag, shorter);
  106.         if(shorter){
  107.             switch(s->bf){
  108.                 case LH://这是上面配图的情况
  109.                     leftBalance_del(s);
  110.                     shorter = false;
  111.                     break;
  112.                 case EH:
  113.                     s->bf = LH;
  114.                     shorter = true;
  115.                     break;
  116.                 case RH:
  117.                     s->bf = EH;
  118.                     shorter = false;
  119.                     break;
  120.             }
  121.         }
  122.     }
  123. } 
  124.  
  125. template <typename ElemType>
  126. bool AVL<ElemType>::insertAVL(BSTNode<ElemType>* &T, ElemType key, bool &taller){
  127.     if(!T){//插入新的节点，taller=true 那么树的高度增加
  128.         T = new BSTNode<ElemType>();
  129.         T->data = key;
  130.         T->bf = EH;
  131.         taller = true;
  132.     } else {
  133.         if(T->data == key){
  134.             taller = false;
  135.             return false;
  136.         }
  137.         if(T->data > key){//向T的左子树进行搜索并插入
  138.             if(!insertAVL(T->child[], key, taller)) return false;
  139.             if(taller){//
  140.                 switch(T->bf){
  141.                     case LH://此时左子树的高度高，左子树上又插入了一个节点，失衡，需要进行调整
  142.                         leftBalance(T);
  143.                         taller = false;//调整之后高度平衡
  144.                         break;
  145.                     case EH:
  146.                         T->bf = LH;
  147.                         taller = true;
  148.                         break;
  149.                     case RH:
  150.                         T->bf = EH;
  151.                         taller = false;
  152.                         break;
  153.                 }
  154.             }
  155.         }
  156.         if(T->data < key) {//向T的右子树进行搜索并插入
  157.             if(!insertAVL(T->child[], key, taller)) return false;
  158.             switch(T->bf){
  159.                 case LH:
  160.                     T->bf = EH;
  161.                     taller = false;
  162.                     break;
  163.                 case EH:
  164.                     T->bf = RH;
  165.                     taller = true;
  166.                     break;
  167.                 case RH:
  168.                     rightBalance(T);
  169.                     taller = false;
  170.                     break;
  171.             }
  172.         }
  173.     }
  174.     return true;
  175. }
  176.  
  177. template <typename ElemType>
  178. void AVL<ElemType>::deleteAVL(BSTNode<ElemType>* &T, ElemType key, bool &shorter){
  179.     if(T->data == key){
  180.         BSTNode<ElemType>*q, s;
  181.         if(!T->child[]){//右子树为空，然后重接其左子树
  182.             q = T;
  183.             T = T->child[];
  184.             shorter = true;//树变矮了
  185.             delete q;
  186.         } else if(!T->child[]){//左子树为空，重接其右子树
  187.             q = T;
  188.             T = T->child[];
  189.             shorter = true;//树变矮了
  190.             delete q;
  191.         } else {//左右子树都非空 ，也就是第三种情况 
  192.             deleteNode(T, T, NULL, true, shorter);
  193.             shorter = true;
  194.         }
  195.     } else if(T->data > key) {//左子树
  196.         deleteAVL(T->child[], key, shorter);
  197.         if(shorter){
  198.             switch(T->bf){
  199.                 case LH:
  200.                     T->bf = EH;
  201.                     shorter = false;
  202.                     break;
  203.                 case RH:
  204.                     rightBalance_del(T);
  205.                     shorter = false;
  206.                     break;
  207.                 case EH:
  208.                     T->bf = RH;
  209.                     shorter = true;
  210.                     break;
  211.             }
  212.         }
  213.     } else if(T->data < key){//右子树
  214.         deleteAVL(T->child[], key, shorter);
  215.         if(shorter){
  216.             switch(T->bf){
  217.                 case LH://这是上面配图的情况
  218.                     leftBalance_del(T);
  219.                     shorter = false;
                        break;
  220.                 case RH:
  221.                     T->bf = EH;
  222.                     shorter = false;
  223.                     break;
  224.                 case EH:
  225.                     T->bf = LH;
  226.                     shorter = true;
  227.                     break;
  228.             }
  229.         }
  230.     }
  231. }
  232.  
  233. template <typename ElemType>
  234. void AVL<ElemType>::leftBalance(BSTNode<ElemType>* &T){
  235.     BSTNode<ElemType>* lchild = T->child[];
  236.     switch(lchild->bf){//检查T的左子树的平衡度，并作相应的平衡处理
  237.         case LH://新节点 插入到 T的左孩子的左子树上，需要对T节点做单旋(右旋)处理
  238.             T->bf = lchild->bf = EH;
  239.             rotateT(T, );
  240.             break;
  241.         case RH://新节点 插入到 T的左孩子的右子树上，需要做双旋处理  1.对lchild节点进行左旋，2.对T节点进行右旋
  242.             BSTNode<ElemType>* rdchild = lchild->child[];
  243.             switch(rdchild->bf){//修改 T 及其左孩子的平衡因子
  244.                 case LH: T->bf = RH; lchild->bf = EH; break;
  245.                 case EH: T->bf = lchild->bf = EH; break;//发生这种情况只能是 rdchild无孩子节点
  246.                 case RH: T->bf = EH; lchild->bf = LH; break;
  247.             }
  248.             rdchild->bf = EH;
  249.             rotateT(T->child[], );//不要写成 rotateT(lc, 0);//这样的话T->lchild不会改变
  250.             rotateT(T, );
  251.             break;
  252.     }
  253. }
  254.  
  255. template <typename ElemType>
  256. void AVL<ElemType>::rightBalance(BSTNode<ElemType>* &T){
  257.     BSTNode<ElemType>* rchild = T->child[];
  258.     switch(rchild->bf){//检查T的左子树的平衡度，并作相应的平衡处理
  259.         case RH://新节点 插入到 T的右孩子的右子树上，需要对T节点做单旋(左旋)处理
  260.             T->bf = rchild->bf = EH;
  261.             rotateT(T, );
  262.             break;
  263.         case LH://新节点 插入到 T的右孩子的左子树上，需要做双旋处理  1.对rchild节点进行右旋，2.对T节点进行左旋
  264.             BSTNode<ElemType>* ldchild = rchild->child[];
  265.             switch(ldchild->bf){//修改 T 及其右孩子的平衡因子
  266.                 case LH: T->bf = EH; rchild->bf = RH; break;
  267.                 case EH: T->bf = rchild->bf = EH; break;//发生这种情况只能是 ldchild无孩子节点
  268.                 case RH: T->bf = LH; rchild->bf = EH; break;
  269.             }
  270.             ldchild->bf = EH;
  271.             rotateT(T->child[], );
  272.             rotateT(T, );
  273.             break;
  274.     }
  275. }
  276.  
  277. template <typename ElemType>
  278. void AVL<ElemType>::leftBalance_del(BSTNode<ElemType>* &T){
  279.     BSTNode<ElemType>* lchild = T->child[];
  280.     switch(lchild->bf){
  281.         case LH:
  282.             T->bf = EH;
  283.             lchild->bf = EH;
  284.             rotateT(T, );
  285.             break;
  286.         case EH:
  287.             T->bf = LH;
  288.             lchild->bf = EH;
  289.             rotateT(T, );
  290.             break;
  291.         case RH://这是上面配图的情况
  292.             BSTNode<ElemType>* rdchild = lchild->child[];
  293.             switch(rdchild->bf){
  294.                 case LH:
  295.                     T->bf = RH;
  296.                     lchild->bf = rdchild->bf = EH;
  297.                     break;
  298.                 case EH:
  299.                     rdchild->bf = T->bf = lchild->bf = EH;
  300.                     break;
  301.                 case RH:
  302.                     T->bf = rdchild->bf = EH;
  303.                     lchild->bf = LH;
  304.                     break;
  305.             }
  306.             rotateT(T->child[], );
  307.             rotateT(T, );
  308.             break;
  309.     }
  310. }
  311.  
  312. template <typename ElemType>
  313. void AVL<ElemType>::rightBalance_del(BSTNode<ElemType>* &T){
  314.     BSTNode<ElemType>* rchild = T->child[];
  315.     BSTNode<ElemType>* ldchild = rchild->child[];
  316.     switch(rchild->bf){
  317.         case LH:
  318.             switch(ldchild->bf){
  319.                 case LH:
  320.                     ldchild->bf = T->bf = EH;
  321.                     rchild->bf = RH;
  322.                     break;
  323.                 case EH:
  324.                     ldchild->bf = T->bf = rchild->bf = EH;
  325.                     break;
  326.                 case RH:
  327.                     rchild->bf = T->bf = EH;
  328.                     ldchild->bf = LH;
  329.                     break;
  330.             }
  331.             rotateT(T->child[], );
  332.             rotateT(T, );
  333.             break;
  334.         case EH:
  335.             //outT(this->T);e EH:
  336.             T->bf = RH;
  337.             rchild->bf = EH;
  338.             rotateT(T, );
  339.             break;
  340.         case RH:
  341.             T->bf = EH;
  342.             rchild->bf = EH;
  343.             rotateT(T, );
  344.             break;
  345.     }
  346. }
  347.  
  348. int main(){
  349.     AVL<int> avl;
  350.     avl.buildT();
  351.     cout<<"平衡二叉树先序遍历如下:"<<endl;
  352.     avl.outT(avl.T);
  353.     cout<<endl;
  354.     bool shorter = false;
  355.     avl.deleteAVL(avl.T, , shorter);
  356.     avl.outT(avl.T);
  357.     return ;
  358. } 
  359.  
  360. /*
  361.  13 24 37 90 53 0
  362.  
  363.  13 24 37 90 53 12 26 0
  364. */

平衡二叉树AVL删除的更多相关文章

  1. 数据结构与算法--从平衡二叉树(AVL)到红黑树

    数据结构与算法--从平衡二叉树(AVL)到红黑树 上节学习了二叉查找树.算法的性能取决于树的形状,而树的形状取决于插入键的顺序.在最好的情况下,n个结点的树是完全平衡的,如下图"最好情况&q ...

  2. 二叉查找树（BST)、平衡二叉树(AVL树)（只有插入说明）

    二叉查找树(BST).平衡二叉树(AVL树)(只有插入说明) 二叉查找树(BST) 特殊的二叉树,又称为排序二叉树.二叉搜索树.二叉排序树. 二叉查找树实际上是数据域有序的二叉树,即对树上的每个结点, ...

  3. 平衡二叉树AVL - 插入节点后旋转方法分析

    平衡二叉树 AVL( 发明者为Adel'son-Vel'skii 和 Landis)是一种二叉排序树,其中每一个节点的左子树和右子树的高度差至多等于1. 首先我们知道,当插入一个节点,从此插入点到树根 ...

  4. Java 树结构实际应用 四（平衡二叉树/AVL树）

    平衡二叉树(AVL 树) 1 看一个案例(说明二叉排序树可能的问题) 给你一个数列{1,2,3,4,5,6},要求创建一颗二叉排序树(BST), 并分析问题所在.  左边 BST 存在的问题分析: ...

  5. 二叉查找树、平衡二叉树(AVL)、B+树、联合索引

    1. [定义] 二叉排序树(二拆查找树)中,左子树都比节点小,右子树都比节点大,递归定义. [性能] 二叉排序树的性能取决于二叉树的层数 最好的情况是 O(logn),存在于完全二叉排序树情况下,其访 ...

  6. C平衡二叉树(AVL)创建和删除

    AVL是最先发明的自平衡二叉查找树算法.在AVL中任何节点的两个儿子子树的高度最大差别为一,所以它也被称为高度平衡树,n个结点的AVL树最大深度约1.44log2n.查找.插入和删除在平均和最坏情况下 ...

  7. 【数据结构】平衡二叉树—AVL树

    (百度百科)在计算机科学中,AVL树是最先发明的自平衡二叉查找树.在AVL树中任何节点的两个子树的高度最大差别为一,所以它也被称为高度平衡树.查找.插入和删除在平均和最坏情况下都是O(log n).增 ...

  8. 数据结构快速回顾——平衡二叉树 AVL （转）

    平衡二叉树(Balanced Binary Tree)是二叉查找树的一个进化体,也是第一个引入平衡概念的二叉树.1962年,G.M. Adelson-Velsky 和 E.M. Landis发明了这棵 ...

  9. 平衡二叉树AVL

    1.定义 平衡二叉树(Balanced Binary Tree)是二叉查找树的一个改进,也是第一个引入平衡概念的二叉树.1962年,G.M. Adelson-Velsky 和 E.M. Landis发 ...

随机推荐

  1. 导入数据经常使用的SQL语句整理整理

    1.事务(基本) GO BEGIN TRY BEGIN TRAN -- 导入数据 COMMIT TRAN END TRY BEGIN CATCH ROLLBACK TRAN END CATCH GO ...

  2. 腾讯网2016回响中国：华清远见荣获2016年度知名IT培训品牌

    12月1日,由腾讯网主办的“2016回响中国·腾讯网教育年度盛典”上,揭晓了“2016腾讯网教育年度总评榜”榜单.高端IT就业培训专家——华清远见教育集团凭借自身优质的高薪IT就业服务优势成功入围,荣 ...

  3. php中echo(),print(),print_r(),var_dump()间的区别

    echo()函数:输出一个或多个字符串.实际上它并不是一个函数,所以不必对它使用括号,直接用echo就行.然而,如果您希望向echo()传递一个以上的参数,使用括号将会生成解析错误.echo()函数比 ...

  4. 关于html5新增的功能（百度）

    HTML5包含以下新增和更新功能: 1. 新增了一种HTML文档类型:<DOCTYPE html>   2. 新增了一些结构化标记的元素(<header>,<nav> ...

  5. Nginx反向代理和负载均衡

    一.Nginx反向代理设置 从80端口转向其他端口反向代理(Reverse Proxy)方式是指以代理服务器来接受internet上的连接请求,然后将请求转发给内部网络上的服务器,并将从服务器上得到的 ...

  6. ExecutorService与ThreadPoolTaskExecutor

    1.ExecutorService private static ExecutorService exec = null; public static ExecutorService getExecu ...

  7. Log4j按级别输出到不同文件

    log4j.properties 文件: log4j.logger.net.sf.hibernate.cache=debug log4j.rootLogger = error,portal_log,s ...

  8. java发送邮件..转

    使用Java应用程序发送E-mail十分简单,但是首先你应该在你的机器上安装JavaMail API 和Java Activation Framework (JAF) . 你可以在 JavaMail ...

  9. tab+tab

    <!DOCTYPE html PUBLIC "-//W3C//DTD XHTML 1.0 Transitional//EN" "http://www.w3.org/ ...

  10. Python 比较两个字符串大小

    python 2中,有cmp(a,b)函数,用于比较两个字符串的大小. 如 >>>a='abc' >>>b='abd' >>>print cmp( ...