[剑指offer] 7. 斐波那契数列 (递归 时间复杂度)

简介：

杨辉三角每条斜线上的数之和就构成斐波那契数列。

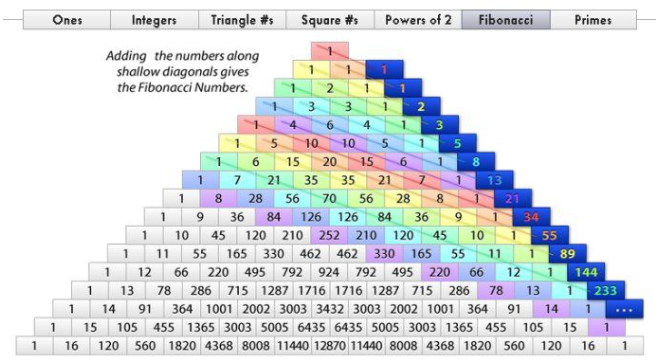
思路:

参考文章：https://mp.weixin.qq.com/s?src=11&timestamp=1551321876&ver=1455&signature=ahEqF*AhQMM5L8e-JCqIGUm6vZ8dQHWSX70P-j-tWtN2gQYpHJSB61cItv2h5Sy-DE0E5grEEVTQikdpIT9tC34u5qLh-mvM*PhBuE3S6nU32*9k1NmkS3krk0YVxRpM&new=1

1.递归法

class Solution:
    def Fibonacci(self, n):
        # write code here
        if n <= 1:
            return n
        while n >= 2:
            return self.Fibonacci(n-1)+self.Fibonacci(n-2)

f(a)会重复计算，这就是递归的最大问题，对于同一个f(a)，不能复用。这样直接求解，时间复杂度是指数级的，不可行；

2.正推法

上述方法是采用反向推导，假设要求f(5)， 则f(5)=f(4)+f(3)； 而f(4)=f(3)+f(2)，f(3)=f(2)+f(1)；.......一路递归下去，最终都将递归到f(0)和f(1)上来。反过来想，我们不倒着f(n),f(n-1),f(n-2)这么计算，而是f(0),f(1),f(2)…f(n)这么正向计算，岂不是更快么？这么正向的计算，只需要一个for循环，就能够计算出f(n)的值，时间复杂度是O(n)。

# -*- coding:utf-8 -*-
class Solution:
    def __init__(self):
        self.array=[0]*40  #数组定义，初始化
    def Fibonacci(self, n):
        # write code here
        self.array[0]=0
        self.array[1]=1
        for i in range(2,n+1):  #直接遍历所有
            self.array[i]=self.array[i-1]+self.array[i-2]
        return self.array[n]

关于数组定义：

• 一维数组：a1 = [0]*10; a2 = range(10)；a3 = [0 for x in range(0, 10)]
• 二维数组：a = [ [ random.random() for x in range(10) ]  for y in range(5)]  #5行10列];  b=[ [ 0 ]*10 ] * 5

在一维数组中，上述几种方式没有区别。

但是在二维数组中，a[0][0]=1时，只有a[0][0]为1，其他全为0。b[0][0]=1时，b[0][0]，b[1][0]...直到b[4,0]全部为1。由此得到二维数组中，若采用b这种定义，每一列数据将全是一个相同的引用，即指向同一地址。故 b = [[0]*10]*5并不符合我们常规意义上的二维数组。

此外还要多种求解方式，复杂度从指数级到O(n) 到 O(lgn) 到 O(1)均有，具体可读参考文章。