Gradle 简介

一、简介

Gradle 是 Android 现在主流的编译工具，虽然在Gradle 出现之前和之后都有对应更快的编译工具出现，但是 Gradle 的优势就在于它是亲儿子，Gradle 确实比较慢，这和它的编译过程有关，但是现在的Gradle 编译速度已经有了成倍提高。除此之外，相对其他编译工具，最重要的，他和 Android Studio 的关系非常紧密，可以说对于一些简单的程序我们几乎不需要任何代码上的配置只使用 Android Studio 就可以完成编译和运行。

官网地址：

https://gradle.org/

下载地址：

http://services.gradle.org/distributions/

 

二、安装配置

1.目前gradle都是绿色版，现在完成后，解压可用

2.为了方便使用，可以设置环境变量

解压 ZIP 文件，本案例解压于 D：\usr\local
、新建环境变量 GRADLE_HOME，即 D：\usr\local\gradle-2.4；
、修改环境变量 Path，即追加 %GRADLE_HOME%\BIN;
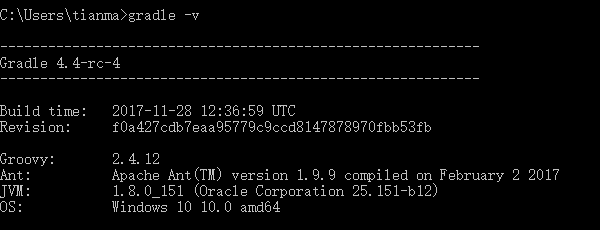
、输入快捷键 WIN+ R，输入 cmd，在弹出的窗口输入命令行： gradle -v；
、创建工程所在目录，本经验创建于 c：\gdemo；
创建空白的 build.gradle 文件，并打开；
、在第一行输入 apply plugin： ‘java’，并执行命令：gradle build。[] 

更多：

Apache Ant 简介和配置

Adb工具常用操作（一）

AndroidSdk下载地址和环境变量配置