在线学习和在线凸优化（online learning and online convex optimization）—凸化方法4

　　一些在线预测问题可以转化到在线凸优化框架中。下面介绍两种凸化技术：

　　一些在线预测问题似乎不适合在线凸优化框架。例如，在线分类问题中，预测域（predictions domain）或损失函数不是凸的。我们描述了两种凸化技术，它们允许我们在其他场景中使用在线凸优化框架。

　　1.Convexification by Randomization

　　为了演示randomization技术，我们考虑一个专家建议的预测问题：每个在线回合中，学习者必须从d位给定专家的建议中进行选择。

　　表示选到的专家，然后学习机收到一个向量，其中表示听从第个专家的建议所遭受的损失，学习机需要支付的损失为。在这种情况下，decision space是离散的，因此非凸。

　　有限假设类（finite hypothesis class）的在线分类问题可以很容易地作为具有专家建议问题的预测的特例。 因此，Cover’s impossibility result意味着没有算法可以通过专家建议问题获得预测的low Regret。

　　然而，正如我们在下面所示，通过允许学习者随机化他的预测，我们可以将问题转化为在线凸优化框架，因此可以获得针对该问题的low Regret算法。令是probability simplex，S是一个凸集。　　

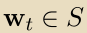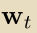　　在第 t回合，学习者选择，并且基于根据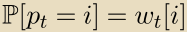随机抽取一个专家，学习机支付期望损失：

　　

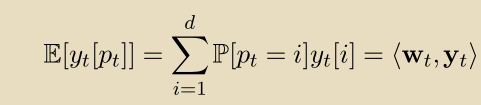
　　现在，我们将问题转化成了在线凸优化。

　　2.Convexification by Surrogate Loss Functions

　　为了解释第二种凸化技术，我们再次从有限假设类的在线分类具体问题开始。 回想一下，我们用来回避 Cover’s impossibility result的技术之一依赖于可实现性假设（realizability assumption）。我们假设存在使得对于所有的t有。有了这个假设，我们描述了Halving算法并且表明它最多个预测错误。我们现在使用在线凸优化语言得出类似的保证:

　　

　　

　　S是一个凸集，对于所有t是一个凸函数，我们转化得到一个在线凸优化问题。

　　接下来的部分中，我们将推导出在线凸优化问题的算法。 特别是，这些算法之一具有如下的regret bound：

　　

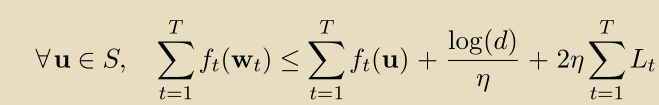
　　其中，是一个参数，在这里设置为1/4，是函数关于L1范数的Lipschitz参数。在我们的案例中，,因此：

　　

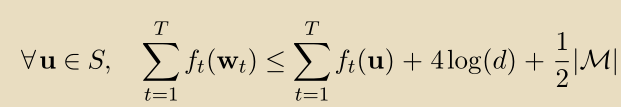
　　通过的 surrogate property，我们获得：

　　

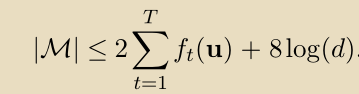
　　这种类型的界限，其中错误的数量受到 competing hypothesis的convex surrogate loss的上限，通常被称为relative loss bound。

　　在realizable的情况下，我们可以进一步简化 relative loss bound如下。 由于bound适用于所有u∈S，因此它特别适用于向量u=(0，...，0,1,0，...，0)，其中1位于对应于 true hypothesis 的位置。

　　 通过我们的构造，对于所有t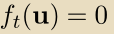，，产生：

　　

　　

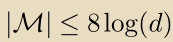
　　未完，待续。。。。。。

　　下一节分析FTL算法