[机器学习]SVM---硬间隔最大化数学原理
注:以下的默认为2分类
1、SVM原理:
(1)输入空间到特征空间得映射
所谓输入空间即是输入样本集合,有部分情况输入空间与特征空间是相同得,有一部分情况二者是不同的,而模型定义都是定义到特征空间的,特征空间是指所有的输入特征向量,特征向量是利用数值来表示的n维向量,输入空间到特征空间的映射,也就是对所用的特征进行数值量化(本人这么理解),与概率中的随机变量是一样的形式,随机变量是由样本空间到实数集的映射,例如:抛硬币的样本空间是{正面,反面},映射到实数集便为{1,0}
(2)求得间隔最大化最优分离超平面
所谓分离超平面,即是能够将所有的特征向量划分为两类的平面或直线(特征有两个变为直线,多个变为平面,即几维的问题),比如二维的情况下,一条线,能够坐标系中的所有点划分为两类,最优意为可以将所有的点尽量进行正确的划分,间隔最大化意为:在两类区域中各自距离直线最近的点到直线的距离是最大的,因此可以求得唯一的间隔最大化最优分离超平面w*x+b*=0,由于是距离因此是由法向量和截距决定,w*为法向量,b*为截距,此处对这个方程进行解释:法向量是从点到平面的垂直方向,在几何中求平面的方程时,平面方程可以设为一般方程Ax+By+Cz+D=0,这便可以看作为(A,B,C)*(x,y,z)即w*=(A,B,C),特征向量x=(x,y,z),b*=D.同理在求直线直线可设为Ax+By+C=0,因此求超平面时即为求w*,b*.
(3)求分类决策函数
所谓分类决策函数只是一个符号函数f(x)=sign(w*x+b*),sign是一个符号函数,取输入值的符号(正负),在上边取得法向量和截距以后与输入特征向量运算后将结果带入sign()得到分类
2、基础概念
(1)函数间隔
上边已经说了是求到超平面的最近距离的点的距离最大的超平面,因此求距离是很重要的一步,根据点到平面的距离公式分子为|w*x+b|,由于分母是相同的,所以|w*x+b|可以相对的表示出距离的大小。y(向量)在此表示的是每个特征向量的分类,而由上边已经知道,分类决策是求的符号的,因此可以确定w*x+b与y的符号(相对应元素)是相同的,因此可以利用y(w*x+b)来表示分类的正确性和确信度,这就是函数间隔: 
注:超平面关于特征空间的函数间隔是值所有特征向量到超平面的函数间隔中的最小值

(2)几何间隔
利用函数间隔来具体衡量时,会出现一个问题,当法向量和截距同时扩大两倍时,超平面不变,但是函数间隔却便为原来的两倍,因此引入几何间隔的概念,其实简单的来说,几何间隔便是函数间隔除以法向量的模,具体公式如下:
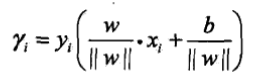
同时由超平面关于特征空间的几何间隔是所有特征向量到超平面的几何间隔中的最小值
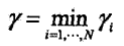
(3)支持向量
在线性可分的情况下,特征空间中距离分离超平面的距离最近的特征向量为支持向量
3、硬间隔最大化的求解方法
这里解释一下何为硬间隔最大化,这个是相对训练数据集或说特征空间来说的,假如数据是完全的线性可分的,则学习到的模型可以称为硬间隔支持向量机,除此之外还有软间隔支持向量机(近似线性可分),非线性支持向量机等,最终的目的都是为了求的w*,b*
(1)最大间隔法推导过程
根据以上的表述可以将求w*和b*归约到两个条件之上,首先求最大的关于特征空间的几何间隔,其次的约束条件为所有的几何间隔必须都大于关于特征空间的几何间隔,则约束最优化问题如下:
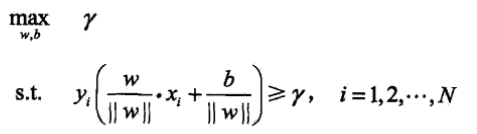
按照几何间隔与函数间隔的关系(都是关于超平面的),这个问题又可以如下表述:

在此可以将以上的式子进行优化,上边的第一个式子的分子(关于超平面函数间隔)会变化,而第二个式子不等号右边的(关于超平面函数间隔)也同样幅度变化,因此w与b也会同样幅度的变化,因此关于超平面的函数间隔变化不会影响上述的式子,因此可以利用1来代替。此时求max(1/||w||)与min(1/2*||w||)是一样的,一个在分母,一个在分子,至于为何会取1/2*||w||^2,求导的时候好计算1/2*2=1,如下:
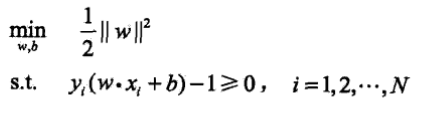
(2)学习的对偶算法
引入拉格朗日对偶性,通过求解对偶问题得到原始问题的最优解,这样做的优点:首先可以降低计算的难度,其次自然引入核函数(非线性可分数据的处理方式)利用拉格朗日对偶性可以构造等价对偶函数(更多请参考统计学习方法),如下:
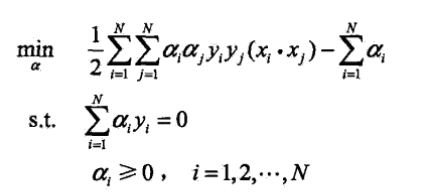
此处由定理用于求w*和b*,如下:
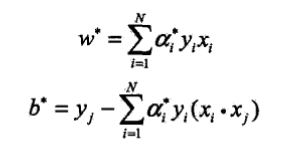
因此根据上边的约束最优化问题即可求的拉格朗日算子,则可求的w*与b*
[机器学习]SVM---硬间隔最大化数学原理的更多相关文章
- SVM中的软间隔最大化与硬间隔最大化
参考文献:https://blog.csdn.net/Dominic_S/article/details/83002153 1.硬间隔最大化 对于以上的KKT条件可以看出,对于任意的训练样本总有ai= ...
- [机器学习&数据挖掘]SVM---软间隔最大化
根据上个硬间隔最大化已经知道,在解决线性可分数据集的分类问题时,求得拉格朗日乘子.w.b就得到分离超平面,然后就可以进行分类,软间隔最大化是针对非线性可分的数据集,因为并不是数据集在可分的时候会出现一 ...
- 《机器学习_07_01_svm_硬间隔支持向量机与SMO》
一.简介 支持向量机(svm)的想法与前面介绍的感知机模型类似,找一个超平面将正负样本分开,但svm的想法要更深入了一步,它要求正负样本中离超平面最近的点的距离要尽可能的大,所以svm模型建模可以分为 ...
- [机器学习&数据挖掘]朴素贝叶斯数学原理
1.准备: (1)先验概率:根据以往经验和分析得到的概率,也就是通常的概率,在全概率公式中表现是“由因求果”的果 (2)后验概率:指在得到“结果”的信息后重新修正的概率,通常为条件概率(但条件概率不全 ...
- 100天搞定机器学习|Day8 逻辑回归的数学原理
机器学习100天|Day1数据预处理 100天搞定机器学习|Day2简单线性回归分析 100天搞定机器学习|Day3多元线性回归 100天搞定机器学习|Day4-6 逻辑回归 100天搞定机器学习|D ...
- SVM中的间隔最大化
参考链接: 1.https://blog.csdn.net/TaiJi1985/article/details/75087742 2.李航<统计学习方法>7.1节 线性可分支持向量机与硬间 ...
- 机器学习——SVM
整理自: https://blog.csdn.net/woaidapaopao/article/details/77806273?locationnum=9&fps=1 带核的SVM为什么能分 ...
- 机器学习,详解SVM软间隔与对偶问题
今天是机器学习专题的第34篇文章,我们继续来聊聊SVM模型. 我们在上一篇文章当中推导了SVM模型在硬间隔的原理以及公式,最后我们消去了所有的变量,只剩下了\(\alpha\).在硬间隔模型当中,样本 ...
- 【机器学习笔记之七】PCA 的数学原理和可视化效果
PCA 的数学原理和可视化效果 本文结构: 什么是 PCA 数学原理 可视化效果 1. 什么是 PCA PCA (principal component analysis, 主成分分析) 是机器学习中 ...
随机推荐
- bower配置私服nexus3
内容来自 https://help.sonatype.com/repomanager3/bower-repositories#BowerRepositories-BrowsingBowerReposi ...
- CentOS Docker环境搭建教程
安装与配置 Docker 安装 Docker Docker 软件包已经包括在默认的 CentOS-Extras 软件源里.因此想要安装 docker,只需要运行下面的 yum 命令: yum inst ...
- 微软职位内部推荐-Senior Development Lead – Sharepoint
微软近期Open的职位: SharePoint is a multi-billion dollar enterprise business that has grown from an on-prem ...
- PAT甲题题解-1120. Friend Numbers (20)-水题
博主欢迎转载,但请给出本文链接,我尊重你,你尊重我,谢谢~http://www.cnblogs.com/chenxiwenruo/p/6789775.html特别不喜欢那些随便转载别人的原创文章又不给 ...
- PAT甲题题解-1128. N Queens Puzzle (20)-做了一个假的n皇后问题
博主欢迎转载,但请给出本文链接,我尊重你,你尊重我,谢谢~http://www.cnblogs.com/chenxiwenruo/p/6789810.html特别不喜欢那些随便转载别人的原创文章又不给 ...
- HDU 2029 算菜价
http://acm.hdu.edu.cn/showproblem.php?pid=2090 Problem Description 妈妈每天都要出去买菜,但是回来后,兜里的钱也懒得数一数,到底花了多 ...
- Docker(十二)-Docker Registry镜像管理
Registry删除镜像.垃圾回收 Docker仓库在2.1版本中支持了删除镜像的API,但这个删除操作只会删除镜像元数据,不会删除层数据.在2.4版本中对这一问题进行了解决,增加了一个垃圾回收命令, ...
- [转帖]Linux系统/dev/mapper目录浅谈
Linux系统/dev/mapper目录浅谈 Linux系统的一般的文件系统名称类似于/dev/sda1或/dev/hda1,但是今天在进行系统维护的时候,利用df -h 命令敲出了/dev/ma ...
- 一本通1623Sherlock and His Girlfriend
1623:Sherlock and His Girlfriend 时间限制: 1000 ms 内存限制: 524288 KB [题目描述] 原题来自:Codeforces Round ...
- 本地开启apache虚拟服务器
一般来说,服务器是可以托管多个网站的,只要服务器开启虚拟主机的功能,原理是根据来源的host进行判断,不同的域名实现不同的文件访问,这样就可以实现一个服务器托管不同网站了,只要服务器的性能和带宽足够强 ...
