Wannafly Camp 2020 Day 3I N门问题 - 概率论,扩展中国剩余定理

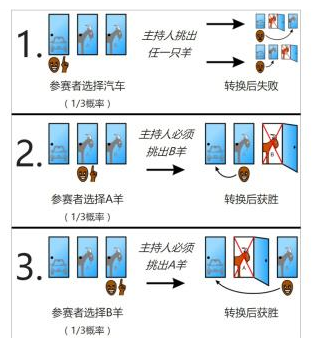
有一个猜奖者和一个主持人，一共有 \(n\) 扇门，只有一扇门后面有奖，主持人事先知道哪扇门后有奖，而猜奖者不知道。每一轮，猜奖者选择它认为的有奖概率最大（如果有多个最大，随机选一个）的一扇门，主持人从剩下的且门后没有奖的门中随机打开一扇。直到剩两扇门时，猜奖者做出的选择就是他最后的选择。

现在由你来安排主持人每次打开哪一扇门，猜奖者不知道有内幕，他还认为主持人是从可以打开的门中随机一扇打开。你要使猜奖者获奖概率最低，求这个概率。

（Discover Probability，你的快乐老家 ）

Solution

这个题真是有趣，一步一步来

当然还是先用个 EXCRT 的板子把外面的数论模型解掉

选手是怎么计算每扇门的概率的？

设现在还有 \(n\) 扇门，第 \(i\) 扇当前的概率是 \(p[i]\) ，不妨设选手选了 \(x\)，主持人打开了 \(y\)

根据样本空间的对称性，\(p[x]\) 保持不变，而 \(p[y]\) 变化为 \(0\)，于是对任意 \(z\neq x,y\)，有 \(p'[z]=p[z] \frac{1-p[x]}{1-p[x]-p[y]}\)

我们顺便发现，由于每次选手选择的门都是当前概率最小的，并且在一波操作后它的概率没变而其它门的概率变大，所以这扇门永远是概率最小的

问题转化

有 \(n\) 个球站队，队分成两段，靠近队头的那段叫做 head，一开始所有的球都在 head 里，所有球中有一个是 good 球，其它球是 bad 球

每次从 head 随机取一个球 \(x\)，从剩下的所有 bad 球中去掉一个，并且把 \(x\) 放到队尾。被追加到队尾的球不再是 head 段中的球

当只剩下两个球的时候，如果 head 球是 good，那么就 WIN，否则就 LOSE

小范围的 DP

设 \(f[i][j][k]\) 表示还剩下 \(i\) 个球，head 中有 \(j\) 个球，good 是队列中第 \(k\) 个球，从这个状态开始玩的最小概率，暴力转移即可，时间复杂度 \(O(n^3)\)

打表

将不同 \(n\) 时的答案打印出来，很容易发现在 \(n>10\) 的时候，选手就必败了

那还等什么，写个暴搜打表交

#include <bits/stdc++.h>
using namespace std;

#define int long long
const int N = 205;

string s[12]={"error","error","0.500000","0.666667","0.625000","0.466667",
    "0.416667","0.342857","0.291667","0.253968","0.225000","0.000000"};

// Input: n,ai[],bi[]
// Method: solve()
// Output: (returned)
namespace excrt {
const int maxn=100010;
int n;
int ai[maxn],bi[maxn]; //x=a%b
int mul(int a,int b,int mod){
    int res=0;
    while(b>0){
        if(b&1) res=(res+a)%mod;
        a=(a+a)%mod;
        b>>=1;
    }
    return res;
}
int exgcd(int a,int b,int &x,int &y){
    if(b==0){x=1;y=0;return a;}
    int gcd=exgcd(b,a%b,x,y);
    int tp=x;
    x=y; y=tp-a/b*y;
    return gcd;
}
int solve(){
    int x,y,k;
    int M=bi[1],ans=ai[1];
    for(int i=2;i<=n;i++){
        int a=M,b=bi[i],c=(ai[i]-ans%b+b)%b;
        int gcd=exgcd(a,b,x,y),bg=b/gcd;
        if(c%gcd!=0) return -1;
        x=mul(x,c/gcd,bg);
        ans+=x*M;
        M*=bg;
        ans=(ans%M+M)%M;
    }
    return (ans%M+M)%M;
}
}

signed main(){
    int n;
    cin>>n;
    excrt::n=n;
    for(int i=1;i<=n;++i) cin>>excrt::ai[i]>>excrt::bi[i]; //x=a%b
    n=excrt::solve();
    cout<<s[min(max(0ll,n),11ll)];
}