Konig定理及证明
Konig定理
证明:
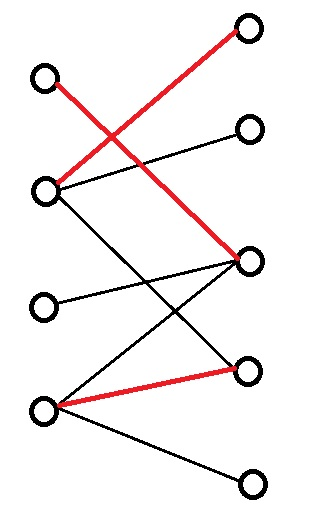
对于上面的二分图，它的最大匹配(不唯一)已经用红线标出来了，
然后我们对于右边或左边(这里按右边为例)没有匹配的点，我们从它出发走交替路(这里有介绍)，会经过若干节点
将所有从右边没有匹配的点开始的交替路上的所有的点标注起来(如下图标蓝的点)
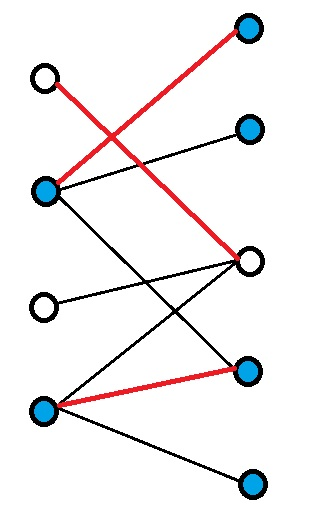
可以证明左边所有被标注的点都是被匹配的点(否则从未匹配的点到未匹配的点的交替路就是增广路)
右边所有没有被标注的点都是被匹配的点(或是没连任何边的点，可以忽略。否则可以从它开始走任意非匹配边，它就会被标注)
这些点就是最小覆盖点集(被标红)
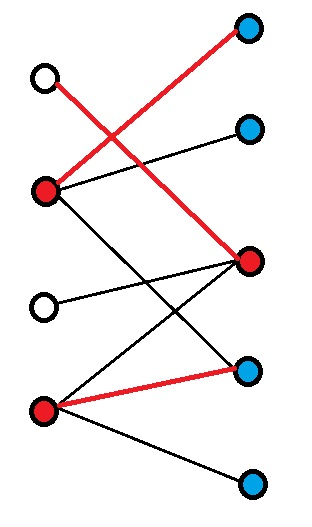
因为对于所有右边被标注的点连的边,其左边的点都被标注了，会被覆盖
假设左边的点是不是匹配点且没被标注，则当前边一定不是匹配边，可以加入交替路中，所以假设不成立
假设左边的点是匹配点且没被标注，则当前边一定是匹配边且不在交替路中，那么右边的这个点也是匹配点且被标记，那么右边的这个点已经连了一个在交替路中的匹配边，但一个点最多会有一个匹配边，所以假设不成立
对于所有左边没被标注的点连的边，其右边的点都没被标注
假设右边的点是匹配点且被标注，则当前边一定不是匹配边，可以加入交替路中，所以假设不成立
假设右边的点不是匹配点且被标注，则当前边一定不是匹配边，可以加入交替路中，所以假设不成立
所以所有边都被覆盖了
Konig定理及证明的更多相关文章
- 二分图最小覆盖的Konig定理及其证明,最小的覆盖证明
[转http://www.cppblog.com/abilitytao/archive/2009/09/02/95147.html -> http://yejingx.ycool.com/p ...
- 【Learning】最小点覆盖（二分图匹配） 与Konig定理证明
(附一道例题) Time Limit: 1000 ms Memory Limit: 128 MB Description 最小点覆盖是指在二分图中,用最小的点集覆盖所有的边.当然,一个二分图的最小 ...
- 二分图最大匹配的König定理及其证明
二分图最大匹配的K?nig定理及其证明 本文将是这一系列里最短的一篇,因为我只打算把K?nig定理证了,其它的废话一概没有. 以下五个问题我可能会在以后的文章里说,如果你现在很想知道的话,网上 ...
- Computer Science Theory for the Information Age-6: 学习理论——VC定理的证明
VC定理的证明 本文讨论VC理论的证明,其主要内容就是证明VC理论的两个定理,所以内容非常的枯燥,但对于充实一下自己的理论知识也是有帮助的.另外,VC理论属于比较难也比较抽象的知识,所以我总结的这些证 ...
- 《University Calculus》-chaper8-无穷序列和无穷级数-泰勒定理的证明
泰勒定理: 证明:
- latex中使用定理、证明、缩进
1.定理和证明 \documentclass[a4paper,UTF8]{article} \usepackage{ctex} \usepackage{amsthm,amsmath,amsfonts, ...
- xdoj-1057(Lucas定理的证明及其模板）
Lucas定理的证明: 转自百度百科(感觉写的还不错) 首先你需要这个算式: ,其中f > 0&& f < p,然后 (1 + x) nΞ(1 + x) sp+q Ξ ...
- hdu5391-Zball in Tina Town-威尔逊定理(假证明)
Tina Town is a friendly place. People there care about each other. Tina has a ball called zball. Zba ...
- 初等数论-Base-2(扩展欧几里得算法，同余，线性同余方程，(附：裴蜀定理的证明))
我们接着上面的欧几里得算法说 扩展欧几里得算法 扩展欧几里德算法是用来在已知a, b求解一组x,y,使它们满足贝祖等式\(^①\): ax+by = gcd(a, b) =d(解一定存在,根据数论中的 ...
随机推荐
- Java类加载器浅述
jdk默认提供了三种类加载器: 1.Bootstrap ClassLoader(引导类加载器): 将<JAVA_HOME>\lib目录下的类库加载到虚拟机内存中,用来加载java的核心库, ...
- Mysql: [Warning] Using a password on the command line interface can be insecure
mysql: [Warning] Using a password on the command line interface can be insecure MySQL 5.6 警告信息 comma ...
- python2与python3编码（练习）
#_author:来童星#date:2019/12/9import jsons='star'a=s.encode('utf8')print(s,type(s))# star <class 'st ...
- Windows 开启win32 控制台
{ AllocConsole(); FILE *Journal = NULL; freopen_s(&Journal, "CONOUT$", &qu ...
- 把云数据库带回家！阿里云发布POLARDB Box数据库一体机
9月26日,2019杭州云栖大会上,阿里云宣布正式推出高性能数据库一体机——POLARDB Box,用户部署在自有数据中心即可享受云数据库的便捷体验,同时还为Oracle等传统数据库用户提供一键迁移功 ...
- thinkphp DEFINE标签
DEFINE标签用于中模板中定义常量,用法如下: 直线电机厂家 <define name="MY_DEFINE_NAME" value="3" /> ...
- 同一个tomcat 两个项目 互相访问接口方法
package com.qif.xdqdm.util; import com.alibaba.fastjson.JSONObject; import java.io.*; import java.ne ...
- 在.net core上，Web网站调用微信支付-统一下单接口（xml传参）一直返回错误：mch_id参数格式错误
这是 微信支付-统一下单 接口文档 一.问题描述 在调用统一下单接口时,报mch_id参数格式错误,但商户ID确实是10位数字正确的,可就是一直报这个错误 返回的错误xml如下: 二.排错过程 1.多 ...
- VS2010-MFC（常用控件：列表视图控件List Control 下）
转自:http://www.jizhuomi.com/software/197.html 上一节是关于列表视图控件List Control的上半部分,简单介绍了列表视图控件,其通知消息的处理和有关结构 ...
- java.sql.SQLSyntaxErrorException: ORA-00932: 数据类型不一致: 应为 NUMBER, 但却获得 BINARY
2019-07-24 17:24:35 下午 [Thread: http-8080-4][ Class:net.sf.ehcache.store.disk.Segment Method: net.sf ...