广义欧拉降幂（欧拉定理）——bzoj3884，fzu1759

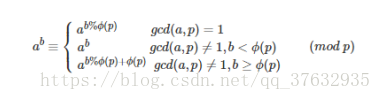
广义欧拉降幂对于狭义欧拉降幂任然适用

https://blog.csdn.net/qq_37632935/article/details/81264965?tdsourcetag=s_pctim_aiomsg

bzoj388

#include<bits/stdc++.h>
using namespace std;
#define ll long long 

ll Pow(ll a,ll b,ll p){
    ll res=;
    while(b){
        if(b%)
            res=res*a%p;
        b>>=;a=a*a%p;
    }
    return res;
}
ll phi(ll x){
    ll res=x,tmp=x;
    for(ll i=;i*i<=tmp;i++)
        if(tmp%i==){
            res=res*(i-)/i;
            while(tmp%i==)tmp/=i;
        }
    if(tmp>)
        res=res*(tmp-)/tmp;
    return res;
}

ll f(ll p){
    if(p==)return ;
    ll q=phi(p);
    return Pow(,q+f(q),p);
}

int main(){
    int t;ll p;cin>>t;
    while(t--){
        cin>>p;
        cout<<f(p)<<'\n';
    }
}

fzu1759 注意在计算phi时要用先除再乘，防止爆精度

#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;
#define ll long long
#define maxn 1000005
char b[maxn];
ll A,C,B;

ll phi(ll x){
    ll res=x,tmp=x;
    for(ll i=;i*i<=tmp;i++)
        if(tmp%i==){
            res=res-res/i;
            while(tmp%i==)
                tmp/=i;
        }
    if(tmp>)
        res=res-res/tmp;
    return res;
}
ll Pow(ll a,ll b,ll p){
    ll res=;
    while(b){
        if(b%)
            res=res*a%p;
        b>>=;a=a*a%p;
    }
    return res;
}

int main(){
    while(cin>>A){
        scanf("%s",b);
        cin>>C;
        ll p=phi(C);
        int len=strlen(b);
        B=;
        for(int i=;i<len;i++)
            B=(B*+b[i]-'')%p;
        cout<<Pow(A,B,C)<<'\n';
    }
}