用OpenGL进行曲线、曲面的绘制
实验目的
- 理解Bezier曲线、曲面绘制的基本原理;理解OpenGL中一维、二维插值求值器的用法。
- 掌握OpenGL中曲线、曲面绘图的方法,对比不同参数下的绘图效果差异;
代码1:用四个控制点绘制一条三次Bezier曲线
#include "stdafx.h"
#include <stdlib.h>
#include <time.h>
#include <GL/glut.h> //4个控制点的3D坐标——z坐标全为0
GLfloat ctrlpoints[][] = {
{ -, -, }, { -, , }, { , -, }, { , , }
}; void init(void)
{
//背景色
glClearColor(0.0, 0.0, 0.0, 1.0);
//将控制点坐标映射为曲线坐标
//参数1:GL_MAP1_VERTEX_3,3维点坐标
//参数2和3:控制参数t或u的取值范围[0, 1]
//参数4:曲线内插值点间的步长3————3维坐标
//参数5:曲线间的补偿为顶点数4个————总步长为12
//参数6:控制点二维数组首元素地址
//注意: 若是在这里设置了相关参数,后续对ctrlpoints内容更改曲线不变
glMap1f(GL_MAP1_VERTEX_3, 0.0, 1.0, , , &ctrlpoints[][]);
//打开开关——允许3维坐标控制点到参数点转换开关
glEnable(GL_MAP1_VERTEX_3);
glShadeModel(GL_FLAT); //代码开关2:去掉本注释,可启用反走样
/*
glEnable(GL_BLEND);
glEnable(GL_LINE_SMOOTH); //允许直线反走样
glHint(GL_LINE_SMOOTH_HINT, GL_FASTEST); // Antialias the lines
glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA);
*/
} void display(void)
{
int i;
glClear(GL_COLOR_BUFFER_BIT);
glColor3f(1.0, 1.0, 1.0); //代码开关1:去掉本注释,查看动态的曲线绘图效果:动态更新控制点坐标
/*
for(int t = 0; t < 4; t++) {
for(int j = 0; j < 3; j++)
ctrlpoints[t][j] = (rand() % 1024 / 1024.0 - 0.5) * 10;
}
//动态映射
glMap1f(GL_MAP1_VERTEX_3, 0.0, 1.0, 3, 4, &ctrlpoints[0][0]);
*/
glLoadIdentity();
glColor3f(1.0, 0.0, 0.0);
//绘制连续线段
glBegin(GL_LINE_STRIP);
//参数t或u取值为i/30,共计31个点
for (i = ; i <= ; i++)
glEvalCoord1f((GLfloat)i / 30.0); //根据4个控制点坐标的参数化插值
glEnd();
/* 显示控制点 */
glPointSize(5.0);
glBegin(GL_POINTS);
for (i = ; i < ; i++)
glVertex3fv(&ctrlpoints[i][]);
glEnd(); glTranslatef(-0.1f, 0.1f, 0.0f);
glColor3f(0.0, 1.0, 0.0);
//glLineWidth(2.0);
//绘制连续线段——线段数越多,曲线越光滑
glBegin(GL_LINE_STRIP);
//设置参数t或u取值为i/60,共计61个点
//实验:若让t从-2变化到+2,可看到什么效果
for (i = ; i <= ; i++)
glEvalCoord1f((GLfloat)i / 60.0); //根据4个控制点坐标的参数化插值
glEnd(); glTranslatef(-0.1f, 0.1f, 0.0f);
glColor3f(1.0, 1.0, 1.0);
//绘制连续线段
glBegin(GL_LINE_STRIP);
//设置参数t或u取值为i/60,共计61个点
//实验:若让t从-2变化到+2,可看到什么效果
for (i = ; i <= ; i++)
glEvalCoord1f((GLfloat)i / 100.0);
glEnd(); glutSwapBuffers();
} //3D空间中绘制2D效果,采用正交投影
void reshape(GLsizei w, GLsizei h)
{
glViewport(, , w, h); glMatrixMode(GL_PROJECTION);
glLoadIdentity();
if (w <= h)
glOrtho(-5.0, 5.0, -5.0*(GLfloat)h / (GLfloat)w, 5.0*(GLfloat)h / (GLfloat)w, -5.0, 5.0);
else
glOrtho(-5.0*(GLfloat)w / (GLfloat)h, 5.0*(GLfloat)w / (GLfloat)h, -5.0, 5.0, -5.0, 5.0); glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
} void keyboard(unsigned char key, int x, int y)
{
switch (key)
{
case 'x':
case 'X':
case : //ESC键
exit();
break;
default:
break;
}
} int main(int argc, char** argv)
{
srand((unsigned int)time());
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_DOUBLE | GLUT_RGB | GLUT_DEPTH);//使用双缓存模式和深度缓存
glutInitWindowSize(, );
glutInitWindowPosition(, );
glutCreateWindow("2D Bezier曲线");
init();
glutDisplayFunc(display);
glutReshapeFunc(reshape);
glutKeyboardFunc(keyboard);
glutIdleFunc(display);//设置空闲时调用的函数
glutMainLoop();
return ;
}
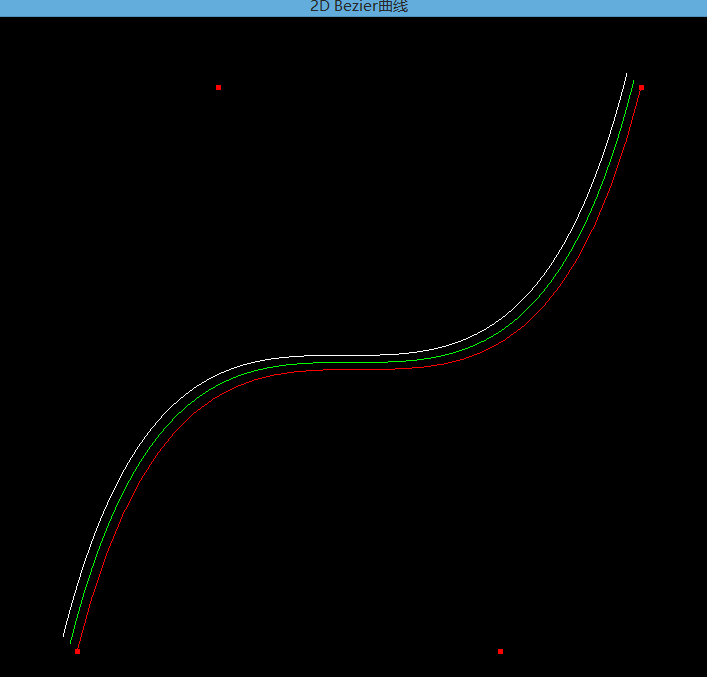
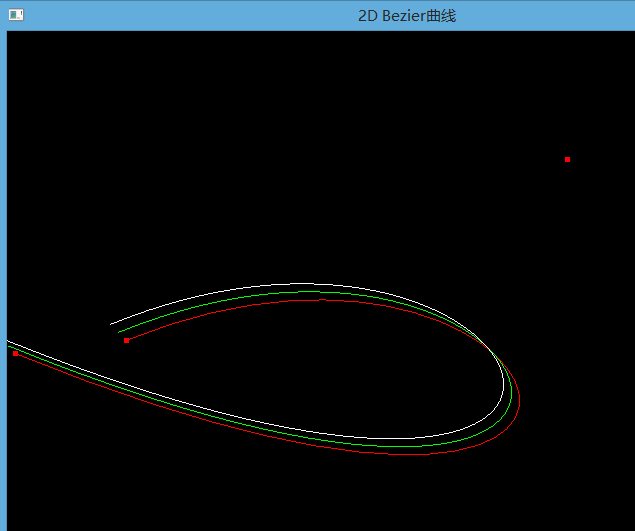
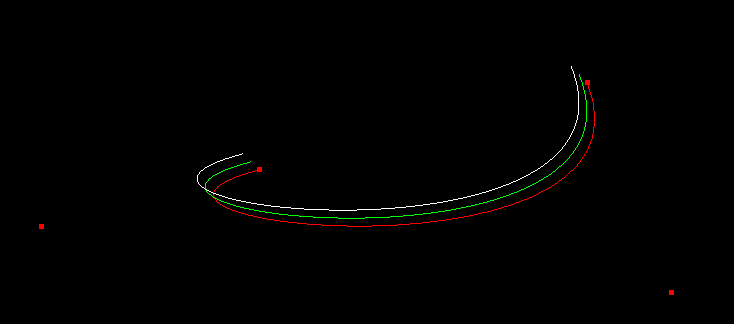
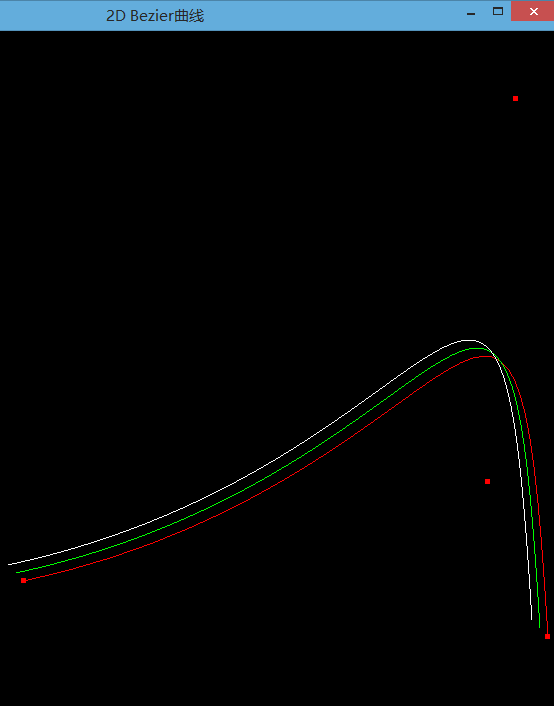
此时我们打开代码开关1,查看动态Bezier曲线绘制效果:
关闭代码开关1,打开代码开关2,查看直线反走样效果:
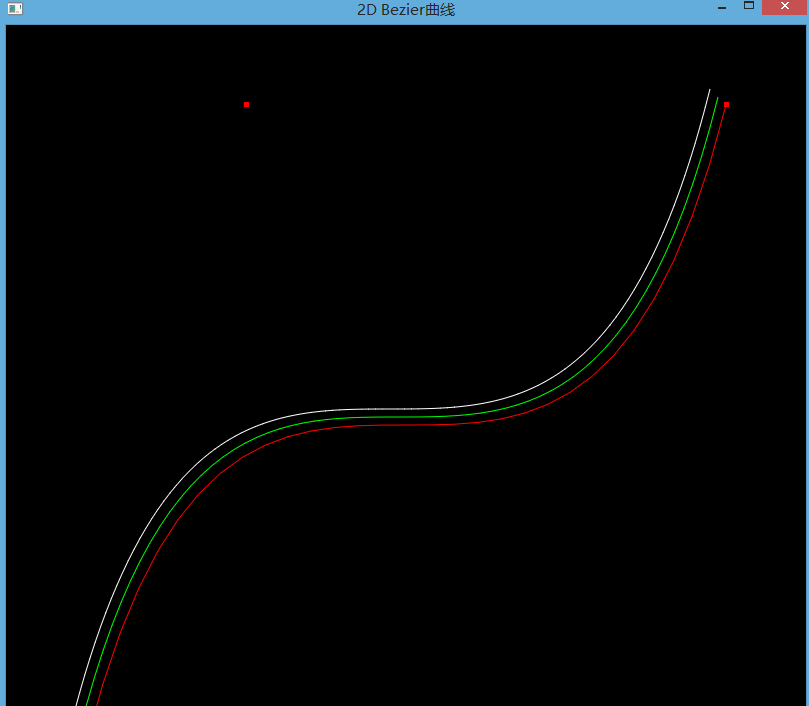
对比刚开始的效果图,我们发现,使用了直线反走样后,绘制出的曲线很光滑,看着很舒服。
代码2:用4*4个控制点绘制一个三次Bezier曲面线框模型
#include "stdafx.h"
#include <stdlib.h>
#include <time.h>
#include <GL/glut.h> /* 控制点的坐标 */
GLfloat ctrlpoints[][][] = {
{ { -1.5, -1.5, 2.0 },
{ -0.5, -1.5, 2.0 },
{ 0.5, -1.5, -1.0 },
{ 1.5, -1.5, 2.0 }
}, { { -1.5, -0.5, 1.0 },
{ -0.5, 1.5, 2.0 },
{ 0.5, 0.5, 1.0 },
{ 1.5, -0.5, -1.0 } }, { { -1.5, 0.5, 2.0 },
{ -0.5, 0.5, 1.0 },
{ 0.5, 0.5, 3.0 },
{ 1.5, -1.5, 1.5 } }, { { -1.5, 1.5, -2.0 },
{ -0.5, 1.5, -2.0 },
{ 0.5, 0.5, 1.0 },
{ 1.5, 1.5, -1.0 } } }; void init(void)
{
//背景色
glClearColor(0.0, 0.0, 0.0, 1.0);
//将控制点坐标映射为曲面坐标
//参数1:GL_MAP1_VERTEX_3,3维点坐标
//参数2和3:控制参数u的取值范围[0, 1]
//参数4:x方向元素间的步长为3个GLfloat
//参数5:x方向曲线间的步长为4个控制点——曲线由4个控制点确定
//参数6-7:控制参数v的取值范围[0, 1]
//参数8:y方向元素间的步长为12个GLfloat元素
//参数9:y方向每条曲线的控制点数量为4
//注意: 若是在这里设置了相关参数,后续对ctrlpoints内容更改曲线不变
glMap2f(GL_MAP2_VERTEX_3, , , , , , , , , &ctrlpoints[][][]);
//允许二维映射
glEnable(GL_MAP2_VERTEX_3);
//二维映射:x、y方向U和V的参数[0, 1],且中间插值数量为各20个
glMapGrid2f(, 0.0, 1.0, , 0.0, 1.0);
//允许深度测试
glEnable(GL_DEPTH_TEST); //代码开关2:启用反走样
glEnable(GL_BLEND);
glEnable(GL_LINE_SMOOTH);
glHint(GL_LINE_SMOOTH_HINT, GL_FASTEST); // Antialias the lines
glBlendFunc(GL_SRC_ALPHA, GL_ONE_MINUS_SRC_ALPHA);
} void display(void)
{
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glColor3f(0.0, 1.0, 0.0);
glPushMatrix();
//代码开关1:去掉注释查看效果;更改旋转角度参数,查看效果
//glRotatef(0.1, 1.0, 1.0, 1.0);
int i, j;
//生成2D网格坐标,以从控制点参数插值确定网格点所对应的点集所对应的坐标
for (j = ; j <= ; j++) {
glBegin(GL_LINE_STRIP);
for (i = ; i <= ; i++)
glEvalCoord2f((GLfloat)i / 30.0, (GLfloat)j / 8.0); //固定y坐标时x方向的网格坐标
glEnd(); glBegin(GL_LINE_STRIP);
for (i = ; i <= ; i++)
glEvalCoord2f((GLfloat)j / 8.0, (GLfloat)i / 30.0); //固定x坐标时y方向的网格坐标
glEnd();
} //查看网格所确定的插值点(u, v)的位置
glColor3f(, , );
glBegin(GL_POINTS);
for (j = ; j <= ; j++) {
for (i = ; i <= ; i++)
glVertex3f((GLfloat)i / 30.0, (GLfloat)j / 8.0, );
for (i = ; i <= ; i++)
glVertex3f((GLfloat)j / 8.0, (GLfloat)i / 30.0, );
}
glEnd();
glPopMatrix();
glutSwapBuffers();
} void reshape(GLsizei w, GLsizei h)
{
glViewport(, , w, h);
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
if (w <= h)
glOrtho(-5.0, 5.0, -5.0*(GLfloat)h / (GLfloat)w, 5.0*(GLfloat)h / (GLfloat)w, -5.0, 5.0);
else
glOrtho(-5.0*(GLfloat)w / (GLfloat)h, 5.0*(GLfloat)w / (GLfloat)h, -5.0, 5.0, -5.0, 5.0);
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
} void keyboard(unsigned char key, int x, int y)
{
switch (key)
{
case 'x':
case 'X':
case : //ESC键
exit();
break;
default:
break;
}
} int main(int argc, char** argv)
{
srand((unsigned int)time());
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_DOUBLE | GLUT_RGB | GLUT_DEPTH);//使用双缓存模式和深度缓存
glutInitWindowSize(, );
glutInitWindowPosition(, );
glutCreateWindow("Bezier曲面线框模型");
init();
glutDisplayFunc(display);
glutReshapeFunc(reshape);
glutKeyboardFunc(keyboard);
glutIdleFunc(display);//设置空闲时调用的函数
glutMainLoop();
return ;
}
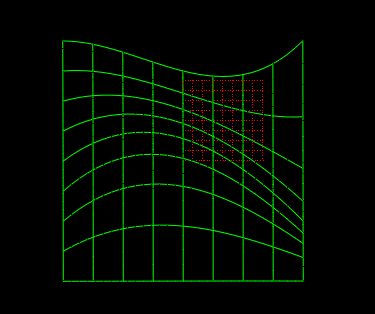
打开代码开关1后的效果:
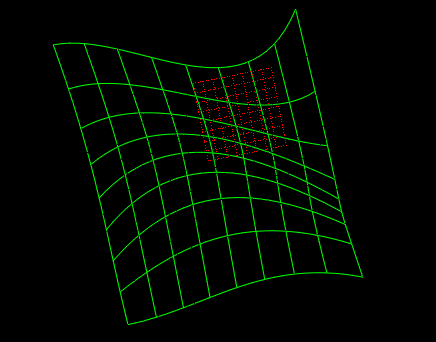
代码3:用4*4个控制点绘制一个三次Bezier曲面并添加光照效果
#include "stdafx.h"
#include <stdlib.h>
#include <time.h>
#include <GL/glut.h>
/* 控制点的坐标 */
GLfloat ctrlpoints[][][] = {
{ { -1.5, -1.5, 2.0 },
{ -0.5, -1.5, 2.0 },
{ 0.5, -1.5, -1.0 },
{ 1.5, -1.5, 2.0 } }, { { -1.5, -0.5, 1.0 },
{ -0.5, 1.5, 2.0 },
{ 0.5, 0.5, 1.0 },
{ 1.5, -0.5, -1.0 } }, { { -1.5, 0.5, 2.0 },
{ -0.5, 0.5, 1.0 },
{ 0.5, 0.5, 3.0 },
{ 1.5, -1.5, 1.5 } }, { { -1.5, 1.5, -2.0 },
{ -0.5, 1.5, -2.0 },
{ 0.5, 0.5, 1.0 },
{ 1.5, 1.5, -1.0 } } }; void init(void)
{
//背景色
glClearColor(0.0, 0.0, 0.0, 1.0);
//将控制点坐标映射为曲面坐标
//参数1:GL_MAP1_VERTEX_3,3维点坐标
//参数2和3:控制参数u的取值范围[0, 1]
//参数4:x方向元素间的步长为3个GLfloat
//参数5:x方向曲线间的步长为4个控制点——曲线由4个控制点确定
//参数6-7:控制参数v的取值范围[0, 1]
//参数8:y方向元素间的步长为12个GLfloat元素
//参数9:y方向每条曲线的控制点数量为4
//note: 若是在这里设置了相关参数,后续对ctrlpoints内容更改曲线不变
glMap2f(GL_MAP2_VERTEX_3, , , , , , , , , &ctrlpoints[][][]);
//允许二维映射
glEnable(GL_MAP2_VERTEX_3);
//二维映射:x、y方向U和V的参数[0, 1],且中间插值数量为各20个
glMapGrid2f(, 0.0, 1.0, , 0.0, 1.0);
//允许深度测试
glDepthFunc(GL_LESS);
glEnable(GL_DEPTH_TEST);
//代码开关4:取消下面两行代码,查看曲面显示效果差异
//打开自动法矢量开关
//glEnable(GL_AUTO_NORMAL);
//允许正则化法矢量
//glEnable(GL_NORMALIZE); //代码开关3:设置材质与光源
GLfloat ambient[] = { 0.4, 0.6, 0.2, 1.0 };
GLfloat position[] = { 0.0, 1.0, 3.0, 1.0 };
GLfloat mat_diffuse[] = { 0.2, 0.4, 0.8, 1.0 };
GLfloat mat_specular[] = { 1.0, 1.0, 1.0, 1.0 };
GLfloat mat_shininess[] = { 80.0 };
glEnable(GL_LIGHTING);
glEnable(GL_LIGHT0);
glLightfv(GL_LIGHT0, GL_AMBIENT, ambient);
glLightfv(GL_LIGHT0, GL_POSITION, position);
glMaterialfv(GL_FRONT, GL_DIFFUSE, mat_diffuse);
glMaterialfv(GL_FRONT, GL_SPECULAR, mat_specular);
glMaterialfv(GL_FRONT, GL_SHININESS, mat_shininess);
} void display(void)
{
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glColor3f(0.0, 1.0, 0.0);
//如果不希望旋转,则启用push和pop矩阵命令,并注释掉glRotatef行
//glPushMatrix();
//代码开关1:去掉注释查看效果;更改旋转角度参数,查看效果
glRotatef(1.0, 1.0, 1.0, 1.0);
glEvalMesh2(GL_FILL, , , , );
//glPopMatrix();
glutSwapBuffers();
} void reshape(GLsizei w, GLsizei h)
{
glViewport(, , w, h);
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
if (w <= h)
glOrtho(-5.0, 5.0, -5.0*(GLfloat)h / (GLfloat)w, 5.0*(GLfloat)h / (GLfloat)w, -5.0, 5.0);
else
glOrtho(-5.0*(GLfloat)w / (GLfloat)h, 5.0*(GLfloat)w / (GLfloat)h, -5.0, 5.0, -5.0, 5.0);
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
} void keyboard(unsigned char key, int x, int y)
{
switch (key)
{
case 'x':
case 'X':
case : //ESC键
exit();
break;
default:
break;
}
} int main(int argc, char** argv)
{
srand((unsigned int)time());
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_DOUBLE | GLUT_RGB | GLUT_DEPTH);//使用双缓存模式和深度缓存
glutInitWindowSize(, );
glutInitWindowPosition(, );
glutCreateWindow("Bezier曲面");
init();
glutDisplayFunc(display);
glutReshapeFunc(reshape);
glutKeyboardFunc(keyboard);
glutIdleFunc(display);//设置空闲时调用的函数
glutMainLoop();
return ;
}

说明
从贝塞尔到B样条
贝塞尔曲线由起点、终点和其他控制点来影响曲线的形状。在二次贝塞尔曲线和三次贝塞尔曲线中,可以通过调整控制点的位置而得到很好的平滑性(C2级连续性 曲率级)的曲线。当增加更多的控制点的时候,这种平滑性就被破坏了。如下图所示,前两个曲线很平滑(曲率级的连续性),第三个曲线在增加了一个控制点之后,曲线被拉伸了,其平滑性遭到了破坏。
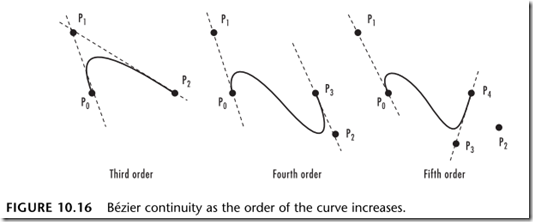
B样条的工作方式类似于贝塞尔曲线,但不同的是曲线被分成很多段。每段曲线的形状只受到最近的四个控制点的影响,这样曲线就像是4阶的贝塞尔曲线拼接起来的。这样很长的有很多控制点的曲线就会有固定的连续性,平滑性(每一段都是c2级的连续性)。
结点
NURBS(非均匀有理B样条)的真正威力在于,可以调整任意一段曲线中的四个控制点的影响力,来产生较好的平滑性。这是通过一系列结点来控制的。每个控制点都定义了两个结点的值。结点的取值范围是u或v的定义域,而且必须是非递减的。
结点的值决定了落在u、v参数定义域内的控制点的影响力。下图的曲线表示控制点对一条在u参数定义域内的具有四个单位的曲线的影响。下图表示中间点对曲线的影响更大,而且只有在[0,3]范围内的控制点才会对曲线产生影响。
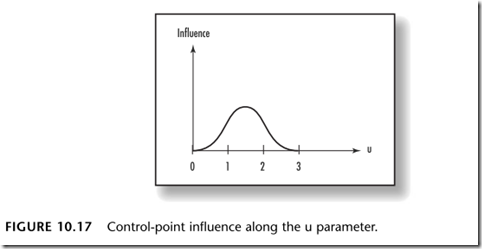
在u、v参数定义域内的控制点对曲线的形状会有有影响,而且我们可以通过结点来控制控制点的影响力。非均匀性就是指一个控制点的影响力的范围是可以改变的。
节点 ( Knot ) 是一个 ( 阶数 + N - 1 ) 的数字列表,N 代表控制点数目。有时候这个列表上的数字也称为节点矢量 ( Knot Vector ),这里的矢量并不是指 3D 方向。
节点列表上的数字必须符合几个条件,确定条件是否符合的标准方式是在列表序列中,数字必需维持不变或变大,而且数字重复的次数不可以比阶数大。例如,阶数 3 有 15 个控制点的 NURBS 曲线,列表数字为 0,0,0,1,2,2,2,3,7,7,9,9,9 是一个符合条件的节点列表。列表数字为 0,0,0,1,2,2,2,2,7,7,9,9,9 则不符合,因为此列表中有四个 2,而四比阶数大 ( 阶数为 3 )。
节点值重复的次数称为节点的重数 ( Multiplicity ),在上面例子中符合条件的节点列表中,节点值 0 的重数值为三;节点值 1 的重数值为一;节点值 2 的重数为三;节点值 7 的重数值为二;节点值 9 的重数值为三。
如果节点值重复的次数和阶数一样,该节点值称为全复节点 ( Full-Multiplicity Knot )。在上面的例子中,节点值 0、2、9 有完整的重数,只出现一次的节点值称为单纯节点 ( Simple Knot ),节点值 1 和 3 为单纯节点。
如果在节点列表中是以全复节点开始,接下来是单纯节点,再以全复节点结束,而且节点值为等差,称为均匀 ( Uniform )。例如,如果阶数为 3 有 7 个控制点的 NURBS 曲线,其节点值为 0,0,0,1,2,3,4,4,4,那么该曲线有均匀的节点。如果节点值是 0,0,0,1,2,5,6,6,6 不是均匀的,称为非均匀 ( Non-Uniform )。在 NURBS 的 NU 代表“非均匀”,意味着在一条 NURBS 曲线中节点可以是非均匀的。
在节点值列表中段有重复节点值的 NURBS 曲线比较不平滑,最不平滑的情形是节点列表中段出现全复节点,代表曲线有锐角。因此,有些设计师喜欢在曲线插入或移除节点,然后调整控制点,使曲线的造型变得平滑或尖锐。因为节点数等于 ( N + 阶数 - 1 ),N 代表控制点的数量,所以插入一个节点会增加一个控制点,移除一个节点也会减少一个控制点。插入节点时可以不改变 NURBS 曲线的形状,但通常移除节点必定会改变 NURBS 曲线的形状。
节点(Knot)与控制点关系:控制点和节点是一对一成对的是常见的错误概念,这种情形只发生在 1 阶的 NURBS ( 多重直线 )。较高阶数的 NURBS 的每 ( 2 x 阶数 ) 个节点是一个群组,每 ( 阶数 + 1 ) 个控制点是一个群组。例如,一条 3 阶 7 个控制点的 NURBS 曲线,节点是 0,0,0,1,2,5,8,8,8,前四个控制点是对应至前六个节点;第二至第五个控制点是对应至第二至第七个节点 0,0,1,2,5,8;第三至第六个控制点是对应至第三至第八个节点 0,1,2,5,8,8;最后四个控制点是对应至最后六个节点
重要:NURB曲面上的裁剪、细分、镶嵌效果,查看网页 https://my.oschina.net/sweetdark/blog/184313
代码4:用4*4个控制点绘制一个NURBS曲面并添加光照效果
#include "stdafx.h"
#include <stdlib.h>
#include <time.h>
#include <GL/glut.h> /* 控制点的坐标 */
GLfloat ctrlpoints[][][] = {
{ { -1.5, -1.5, 2.0 },
{ -0.5, -1.5, 2.0 },
{ 0.5, -1.5, -1.0 },
{ 1.5, -1.5, 2.0 } }, { { -1.5, -0.5, 1.0 },
{ -0.5, 1.5, 2.0 },
{ 0.5, 0.5, 1.0 },
{ 1.5, -0.5, -1.0 } }, { { -1.5, 0.5, 2.0 },
{ -0.5, 0.5, 1.0 },
{ 0.5, 0.5, 3.0 },
{ 1.5, -1.5, 1.5 } }, { { -1.5, 1.5, -2.0 },
{ -0.5, 1.5, -2.0 },
{ 0.5, 0.5, 1.0 },
{ 1.5, 1.5, -1.0 } } }; GLUnurbsObj *theNurb; // 指向一个NURBS曲面对象的指针 void init(void)
{
//背景色
glClearColor(0.0, 0.0, 0.0, 1.0);
//代码开关3:设置材质与光源
GLfloat ambient[] = { 0.4, 0.6, 0.2, 1.0 };
GLfloat position[] = { 1.0, 1.0, 3.0, 1.0 };
GLfloat mat_diffuse[] = { 0.8, 0.6, 0.3, 1.0 };
GLfloat mat_specular[] = { 0.8, 0.6, 0.3, 1.0 };
GLfloat mat_shininess[] = { 45.0 }; glEnable(GL_LIGHTING);
glEnable(GL_LIGHT0);
glLightfv(GL_LIGHT0, GL_AMBIENT, ambient);
glLightfv(GL_LIGHT0, GL_POSITION, position);
glMaterialfv(GL_FRONT, GL_DIFFUSE, mat_diffuse);
glMaterialfv(GL_FRONT, GL_SPECULAR, mat_specular);
glMaterialfv(GL_FRONT, GL_SHININESS, mat_shininess); //允许深度测试
glDepthFunc(GL_LESS);
glEnable(GL_DEPTH_TEST);
//代码开关4:取消下面两行代码,查看曲面显示效果差异
//打开自动法矢量开关
glEnable(GL_AUTO_NORMAL);
//允许正则化法矢量
glEnable(GL_NORMALIZE);
theNurb = gluNewNurbsRenderer(); // 创建一个NURBS曲面对象
//修改NURBS曲面对象的属性——glu库函数
////采样sampling容错torerance
gluNurbsProperty(theNurb, GLU_SAMPLING_TOLERANCE, 5.0);
gluNurbsProperty(theNurb, GLU_DISPLAY_MODE, GLU_FILL);
} void display(void)
{
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glColor3f(0.0, 1.0, 0.0);
//各控制点影响力参数设置
GLfloat knots[] = { 0.0, 0.0, 0.0, 0.0,
1.0, 1.0, 1.0, 1.0 }; // NURBS曲面的控制向量
glRotatef(1.0, 0.7, -0.6, 1.0); // 旋转变换
gluBeginSurface(theNurb); // 开始曲面绘制
//网络查询:参数GL_MAP2_VERTEX_3的作用?
//将
gluNurbsSurface(theNurb, , knots, , knots, * , , &ctrlpoints[][][], , , GL_MAP2_VERTEX_3); // 定义曲面的数学模型,确定其形状
gluEndSurface(theNurb); // 结束曲面绘制
glutSwapBuffers();
} void reshape(GLsizei w, GLsizei h)
{
glViewport(, , w, h);
glMatrixMode(GL_PROJECTION);
glLoadIdentity();
if (w <= h)
glOrtho(-5.0, 5.0, -5.0*(GLfloat)h / (GLfloat)w, 5.0*(GLfloat)h / (GLfloat)w, -5.0, 5.0);
else
glOrtho(-5.0*(GLfloat)w / (GLfloat)h, 5.0*(GLfloat)w / (GLfloat)h, -5.0, 5.0, -5.0, 5.0);
glMatrixMode(GL_MODELVIEW);
glLoadIdentity();
} void keyboard(unsigned char key, int x, int y)
{
switch (key)
{
case 'x':
case 'X':
case : //ESC键
exit();
break;
default:
break;
}
} int main(int argc, char** argv)
{
srand((unsigned int)time());
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_DOUBLE | GLUT_RGB | GLUT_DEPTH);//使用双缓存模式和深度缓存
glutInitWindowSize(, );
glutInitWindowPosition(, );
glutCreateWindow("Bezier曲面"); init(); glutDisplayFunc(display);
glutReshapeFunc(reshape);
glutKeyboardFunc(keyboard);
glutIdleFunc(display);//设置空闲时调用的函数 glutMainLoop();
return ;
}

写在最后
此文是源自学校图形学课程的实验教学内容,我很喜欢这节内容,于是将其源代码和原理整理了出来供感兴趣的人一起学习探讨。
图形学的课程结束后,我的内心却久久不能平静,因为这次课程我似乎找到了我感兴趣的方向——图形学,它给我的感觉就像是技术和艺术的结合。
记得刚开始上图形学课程,老师一直在推导公式,讲解每一个算法中所蕴含的数学原理,使我不禁感觉在上一堂数学课,不过也正因为如此,我才逐渐体会到高等数学和线性代数的作用,为此更加激起了我学习数学的兴趣。
我一直相信——学习和做事的本质是相通的:熟能生巧,勤能补拙,念念不忘,必有回响。^_^
用OpenGL进行曲线、曲面的绘制的更多相关文章
- TWaver3D直线、曲线、曲面的绘制
插播一则广告(长期有效) TWaver需要在武汉招JavaScript工程师若干 要求:对前端技术(JavasScript.HTML.CSS),对可视化技术(Canvas.WebGL)有浓厚的兴趣 基 ...
- 7.5.5编程实例-Bezier曲线曲面绘制
(a)Bezier曲线 (b) Bezier曲面 1. 绘制Bezier曲线 #include <GL/glut.h> GLfloat ct ...
- 从零开始openGL—— 二、 基本图形绘制
前言 这是从零开始openGL系列文章的第二篇,在上篇文章中介绍了基本的环境配置,这篇文章将介绍如何绘制基本图形(圆.三角形.立方体.圆柱.圆锥). 基本框架 下面这里我先给出opengl的3D绘图的 ...
- 基于OpenGL的三维曲面动态显示实现
在使用Visual C++的MFC AppWizard建立应用程序框架后,生成了多个类,与OpenGL编程相关的类是视图类,主要的显示任务都在其中完成. 1.基于OpenGL绘图的基本设置 1.1 设 ...
- opengl es中不同的绘制方式
opengl es中不同的绘制方式 转载请保留出处:http://xiaxveliang.blog.163.com/blog/static/297080342013467344263/ 1. GL_P ...
- OpenGL入门学习 课程 (三) 绘制几何图形的一些细节问题
http://oulehui.blog.163.com/blog/static/79614698201191832753312/ 先回顾一下我们都学习了些什么: 第一课,编写第一个OpenGL程序第二 ...
- openGL加载obj文件+绘制大脑表层+高亮染色
绘制大脑表层并高亮染色的工作是以openGL加载obj文件为基础的,这里是我们用到的原始程序:只能加载一个obj文件的demo. 然而,一个完整的大脑表层是由很多分区组成的,因此我们的程序需要支持两个 ...
- 使用C#三维图形控件进行曲线曲面分析
使用AnyCAD.Net三维图图形控件能够计算曲线的切线.法线.曲率.长度等,能够计算曲面的uv切线.法线.面积等. 代码示例一:曲线分析 Platform.LineStyle lineStyle = ...
- Android OpenGL ES(十一)绘制一个20面体 .
前面介绍了OpenGL ES所有能够绘制的基本图形,点,线段和三角形.其它所有复杂的2D或3D图形都是由这些基本图形构成. 本例介绍如何使用三角形构造一个正20面体.一个正20面体,有12个顶点,20 ...
随机推荐
- scope_identity() 与 @@identity的区别
在一条 INSERT.SELECT INTO 或大容量复制语句完成后,@@IDENTITY 中包含语句生成的最后一个标识值.如果语句未影响任何包含标识列的表,则 @@IDENTITY 返回 NULL. ...
- 每日英语:How Pop Culture Influences Chinese Travelers
Where are Chinese tourists going to next? Pop culture may hold some clues, from blockbuster rom-com ...
- Scala中的foreach forall exists map函数及其区别
forall 对集合中的元素进行某个判断,全部为true则返回true,反之返回false. 例如: scala> var s = List("hello", "w ...
- Beginning SDL 2.0(4) YUV加载及渲染
本文主要内容是基于的“Beginning SDL 2.0(3) SDL介绍及BMP渲染”(以下简称BS3)基础上,将BMP加载及渲染修改为YUV420或I420的原始视频格式.阅读完本部分内容相信你可 ...
- Django服务端读取excel文件并且传输到接口
path_name = "opboss_download_" + str(int(time.time())) + ".csv" print(path_name) ...
- poj2965(位运算压缩+bfs+记忆路径)
题意:有个4*4的开关,里面有着16个小开关 -+-- ---- ---- '+'表示开关是关着的,'-'表示开关是开着的,只有所有的开关全被打开,总开关才会被打开.现在有一种操作,只要改变某个开关, ...
- django 事务错误 -- Transaction managed block ended with pending COMMIT/ROLLBACK
Request Method: GET Request URL: http://192.168.128.111:8000/×××/××××/ Django Version: 1.4.8 Excepti ...
- sparkonhbase
import org.apache.hadoop.hbase.HBaseConfiguration import org.apache.hadoop.hbase.client.Result impor ...
- # Writing your first Django app, part 2
创建admin用户 D:\desktop\todoList\Django\mDjango\demoSite>python manage.py createsuperuser 然后输入密码 进入a ...
- PHP写的一个轻量级的DI容器类(转)
理解什么是Di/IoC,依赖注入/控制反转.两者说的是一个东西,是当下流行的一种设计模式.大致的意思就是,准备一个盒子(容器),事先将项目中可能用到的类扔进去,在项目中直接从容器中拿,也就是避免了直接 ...
