机器学习理论基础学习12---MCMC

　　作为一种随机采样方法，马尔科夫链蒙特卡罗（Markov Chain Monte Carlo，以下简称MCMC）在机器学习,深度学习以及自然语言处理等领域都有广泛的应用，是很多复杂算法求解的基础。比如分解机(Factorization Machines)推荐算法，还有前面讲到的受限玻尔兹曼机（RBM）原理总结，都用到了MCMC来做一些复杂运算的近似求解。下面我们就对MCMC的原理做一个总结。

一、MCMC概述

　　从名字我们可以看出，MCMC由两个MC组成，即蒙特卡罗方法（Monte Carlo Simulation，简称MC）和马尔科夫链（Markov Chain ，也简称MC）。要弄懂MCMC的原理我们首先得搞清楚蒙特卡罗方法和马尔科夫链的原理。我们将用三篇来完整学习MCMC。在本篇，我们关注于蒙特卡罗方法。

二、蒙特卡罗方法引入

　　蒙特卡罗原来是一个赌场的名称，用它作为名字大概是因为蒙特卡罗方法是一种随机模拟的方法，这很像赌博场里面的扔骰子的过程。最早的蒙特卡罗方法都是为了求解一些不太好求解的求和或者积分问题。比如积分：

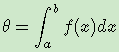
如果我们很难求解出f(x)的原函数，那么这个积分比较难求解。当然我们可以通过蒙特卡罗方法来模拟求解近似值。如何模拟呢？假设我们函数图像如下图:

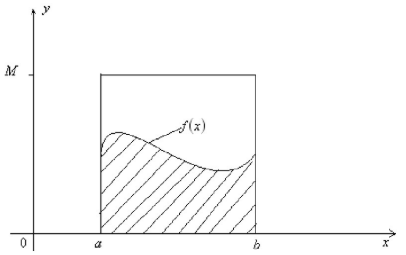
三、MC采样方法

MC采样需要解决：如何根据z的分布p(z)采样出若干样本

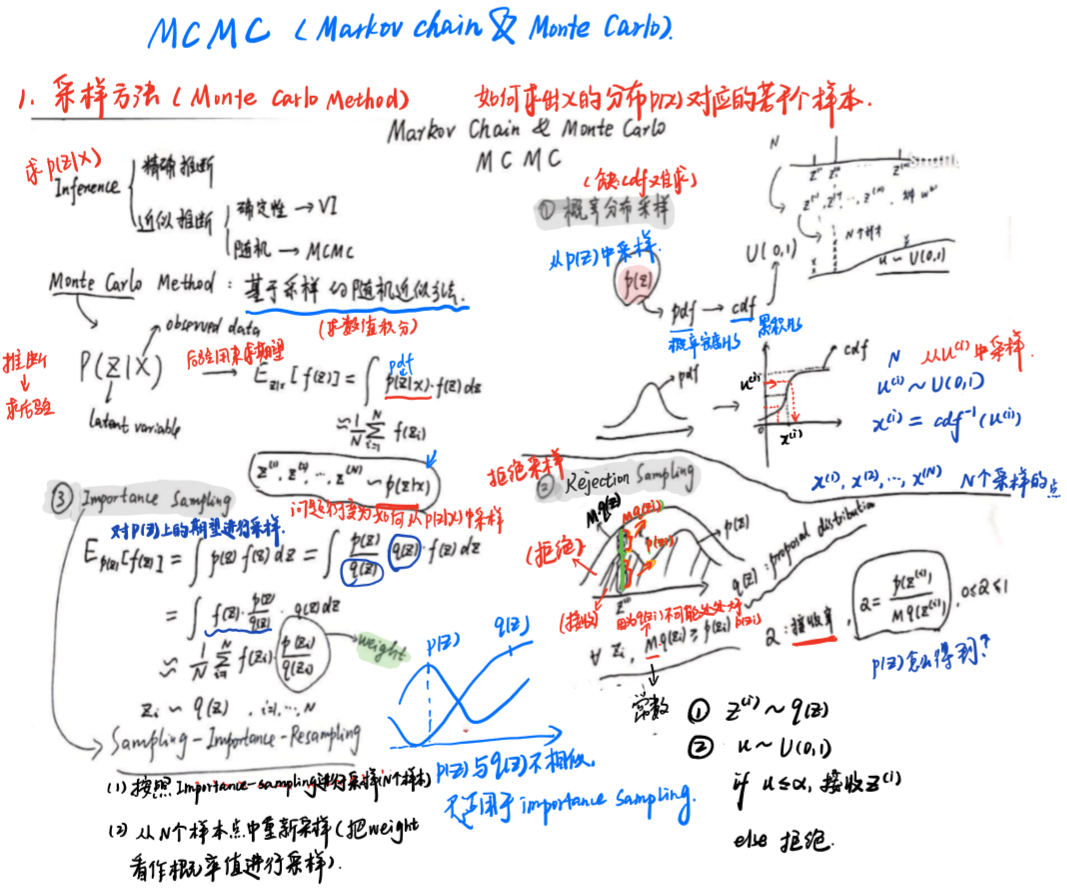
1、概率分布采样（ 适用于已知概率分布，且概率分布是常见的分布）

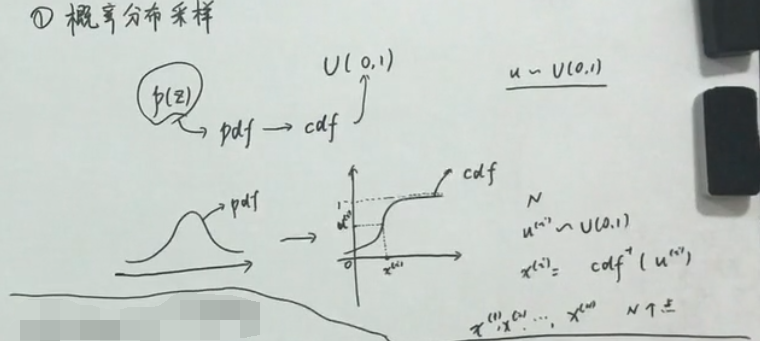
2、接受-拒绝采样（适用于已知概率分布，但概率分布不常见）

既然 p(z) 太复杂在程序中没法直接采样，那么我设定一个程序可采样的分布 q(z) 比如高斯分布，然后按照一定的方法拒绝某些样本，以达到接近 p(z) 分布的目的，其中q(z)叫做 proposal distribution。

 

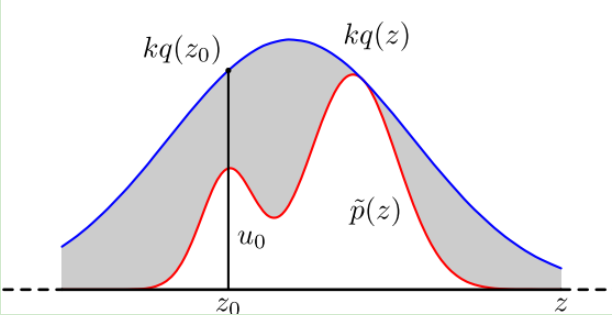
使⽤用接受-拒绝采样，我们可以解决一些概率分布不是常见的分布的时候，得到其采样集并⽤用蒙特卡罗方法求和的目的。但是接受-拒绝采样也只能部分满⾜足我们的需求，在很多时候我们还是很难得到我们的概率分布的样本集。比如：
1）对于一些二维分布p(x,y)，有时候我们只能得到条件分布p(x|y)和p(y|x)和,却很难得到二维 分布p(x,y)⼀一般形式，这时我们无法用接受-拒绝采样得到其样本集。

2）对于一些高维的复杂非常见分布p(x1,x2,...找到一个合适的q(x)和k非常困难。

从上⾯可以看出，要想将蒙特卡罗方法作为一个通用的采样模拟求和的方法，必须解决如何方便便得到各种复杂概率分布的对应的采样样本集的问题。而第四节要讲到的马尔科夫链就是帮助找到这些复杂概率分布的对应的采样样本集的白衣骑士。

3、Importance Sampling

很多时候无法从p(z)中采样，转换为从简单的易采样的分布q(z)中采样,q(z)称为提议分布，proposed distribution。

不是对概率分布进行采样，而是直接对概率分布的期望进行采样。

4、Sampling-Importance-Resampling

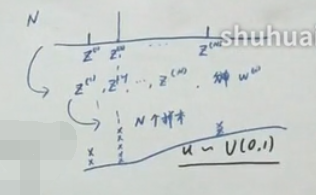
两个阶段：

（1）按照Importance Sampling采样N个样本；

（2）从N个样本中重新采样（把weight看做概率值进行采样）

四、MCMC

1、基于马尔科夫链采样

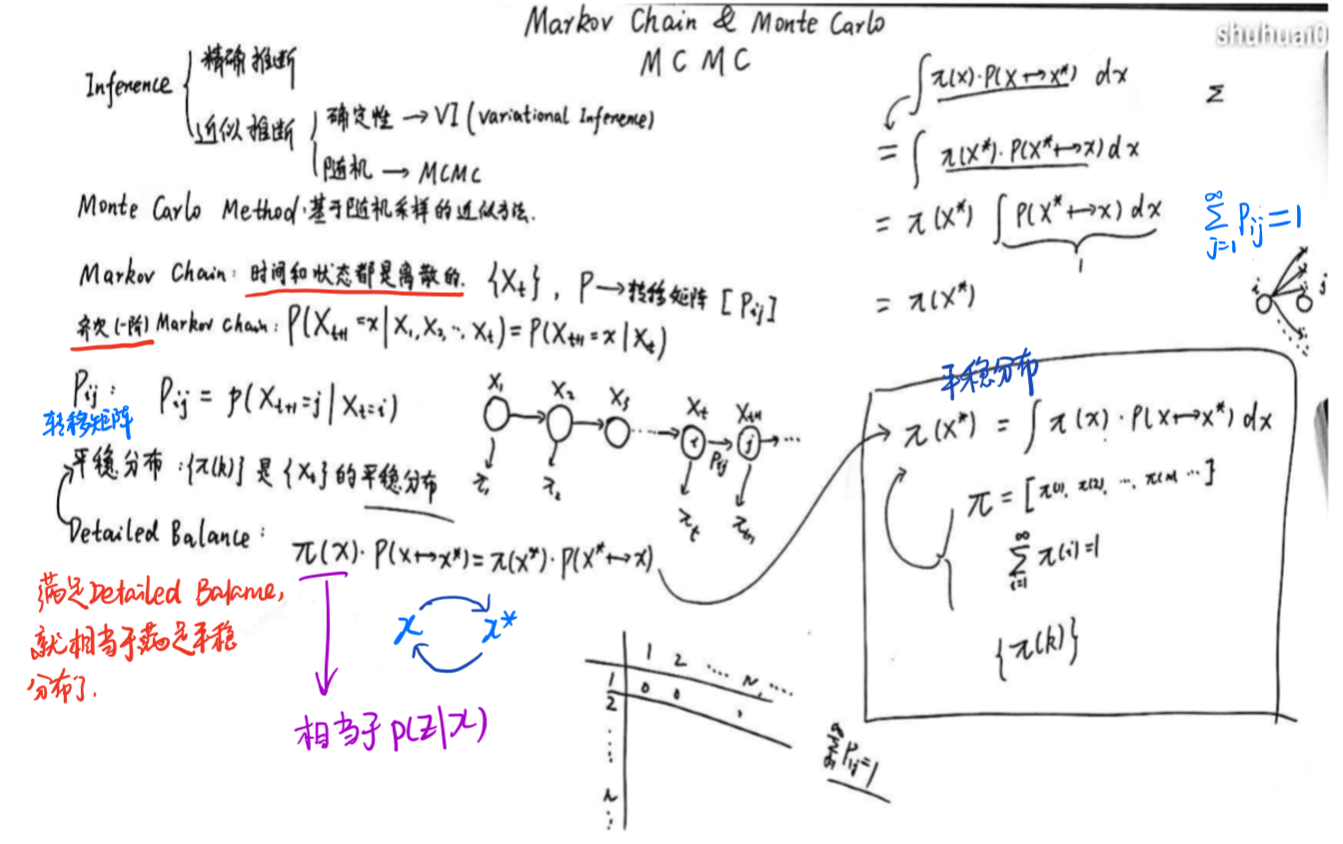
马尔科夫链的收敛性质：

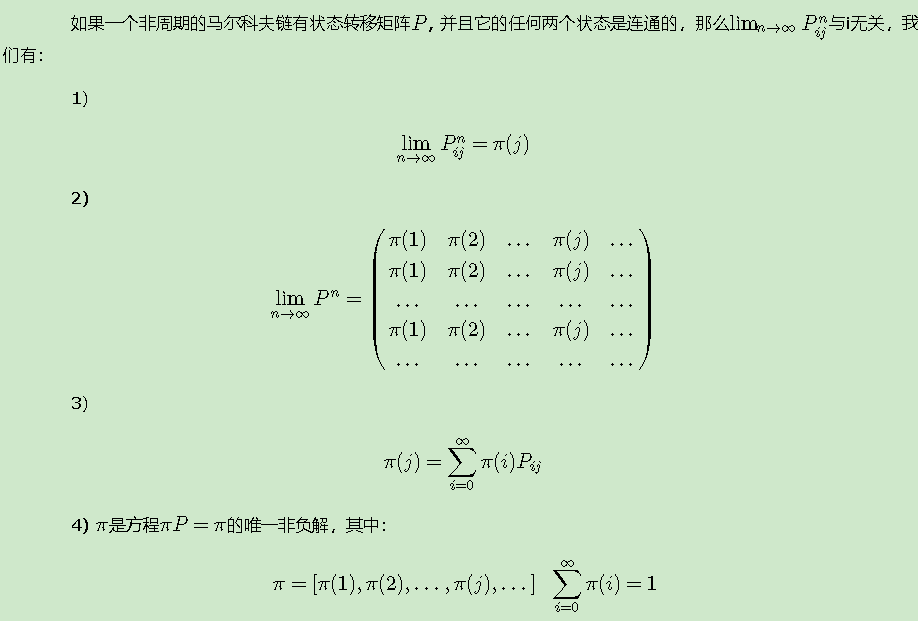
如果我们得到了某个平稳分布所对应的马尔科夫链状态转移矩阵，我们就很容易采用出这个平稳分布的样本集。

　　如果假定我们可以得到我们需要采样样本的平稳分布所对应的马尔科夫链状态转移矩阵，那么我们就可以用马尔科夫链采样得到我们需要的样本集，进而进行蒙特卡罗模拟。但是一个重要的问题是，随意给定一个平稳分布π,如何得到它所对应的马尔科夫链状态转移矩阵P呢？这是个大问题。我们绕了一圈似乎还是没有解决任意概率分布采样样本集的问题。幸运的是，MCMC采样通过迂回的方式解决了上面这个大问题，我们在下一节来讨论MCMC的采样，以及它的使用改进版采样: M-H采样和Gibbs采样.

2、MCMC采样

（1）马尔科夫链的细致平稳条件：

（2）MCMC采样

3、MH采样（Metropolis-Hastings）

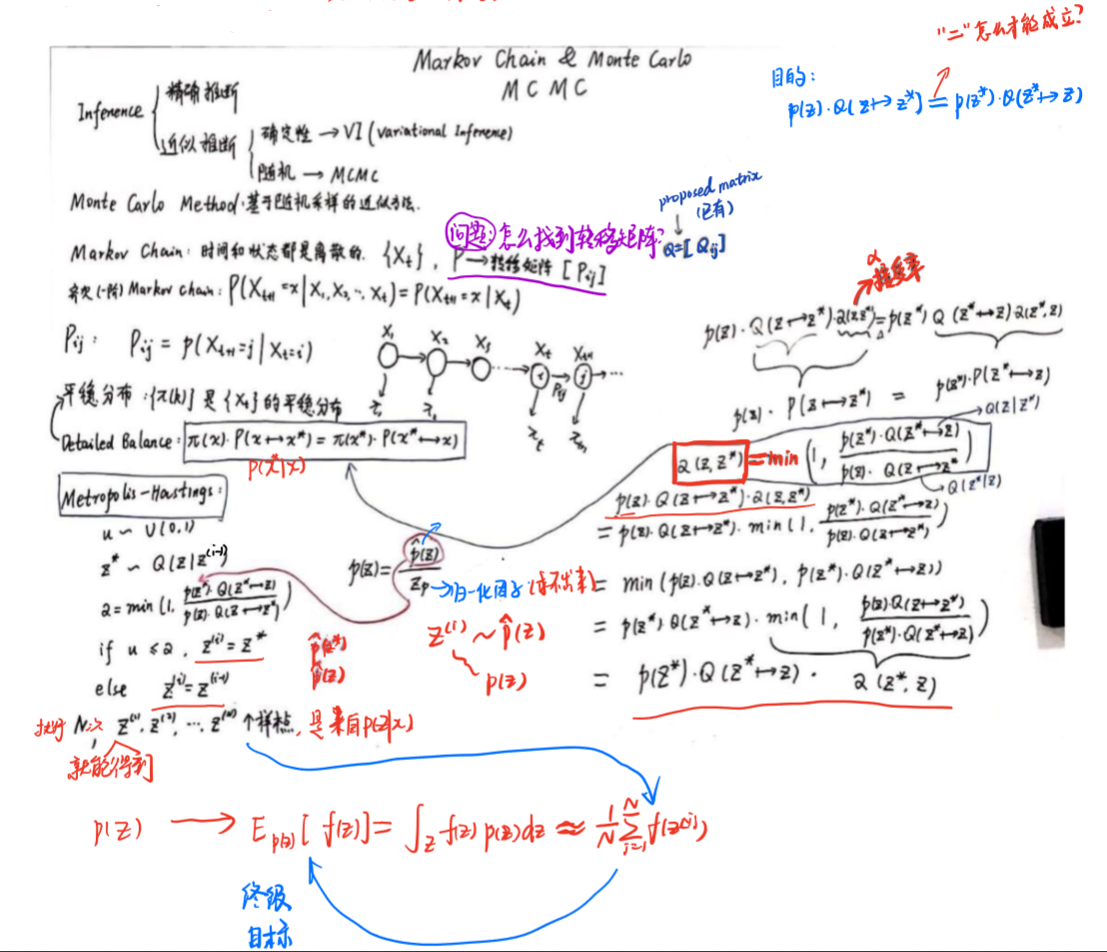
（1）M-H采样

M-H采样解决了我们上一节MCMC采样接受率过低的问题。

（2）总结：

4、吉普斯采样（Gibbs）

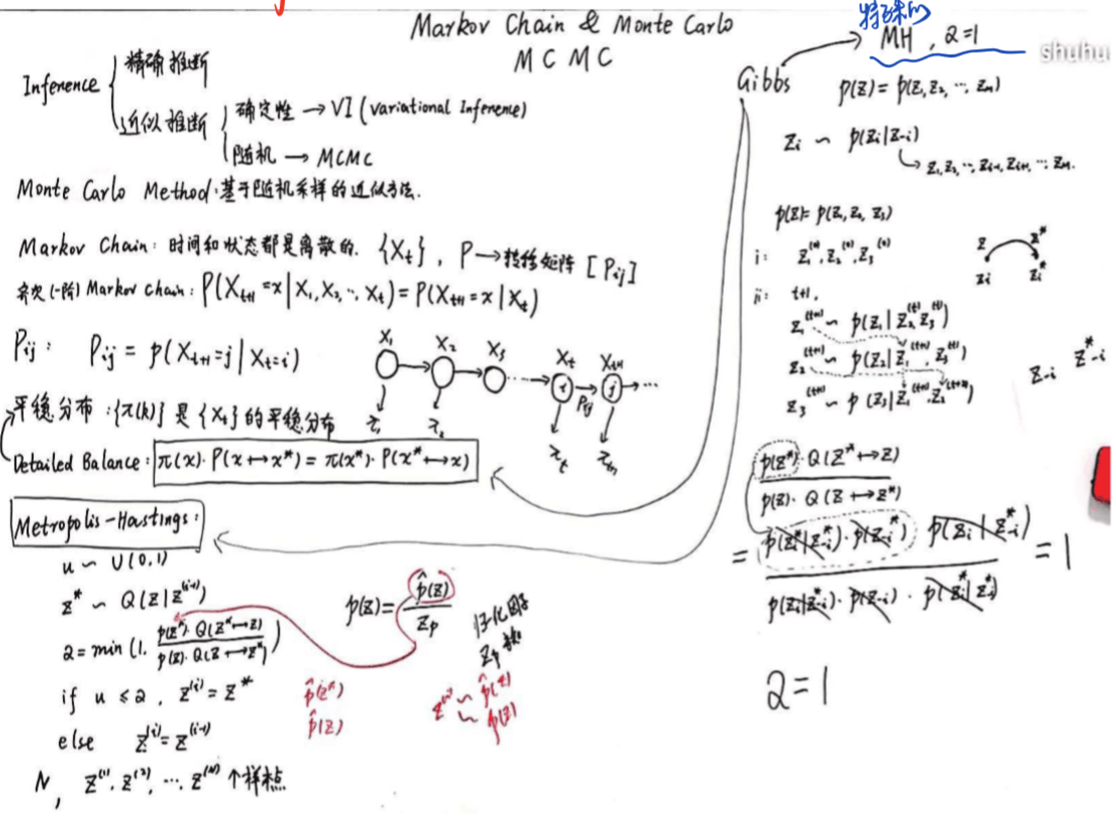
M-H采样已经可以很好的解决蒙特卡罗方法需要的任意概率分布的样本集的问题。但是M-H采样有两个缺点：一是需要计算接受率，在高维时计算量大。并且由于接受率的原因导致算法收敛时间变长。二是有些高维数据，特征的条件概率分布好求，但是特征的联合分布不好求。因此需要一个好的方法来改进M-H采样，这就是我们下面讲到的Gibbs采样。

（1）重新寻找合适的细致平稳条件

（2）二维Gibbs采样

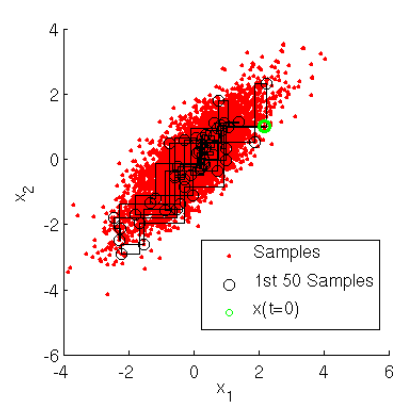
（3）多维Gibbs采样

（4）Gibbs采样小结

由于Gibbs采样在高维特征时的优势，目前我们通常意义上的MCMC采样都是用的Gibbs采样。当然Gibbs采样是从M-H采样的基础上的进化而来的，同时Gibbs采样要求数据至少有两个维度，一维概率分布的采样是没法用Gibbs采样的,这时M-H采样仍然成立。有了Gibbs采样来获取概率分布的样本集，有了蒙特卡罗方法来用样本集模拟求和，他们一起就奠定了MCMC算法在大数据时代高维数据模拟求和时的作用。

参考文献：

【1】MCMC(一)蒙特卡罗方法

【2】马尔可夫链蒙特卡罗算法（MCMC）

【3】告别数学公式，图文解读什么是马尔可夫链蒙特卡罗方法（MCMC）

【4】贝叶斯集锦（3）：从MC、MC到MCMC