图论最短路——dijkstra

下午直接开始dijkstra的堆优化，很简单的这里把书上的原理说一下吧，小心和prim最小生成树的堆优化迷，Dijkstra算法基于贪心思想，它只适用于所有边都是非负数的图。当变长z都是非负数的时候，全局最小值不可能在被其他节点更新，故在第一步中选出的节点x必然满足：dis[x]已经是起点到x的最短路径。我们不断选择全局最小值进行标记和扩展，最终可得到起点s到每个节点的最短路径的长度。

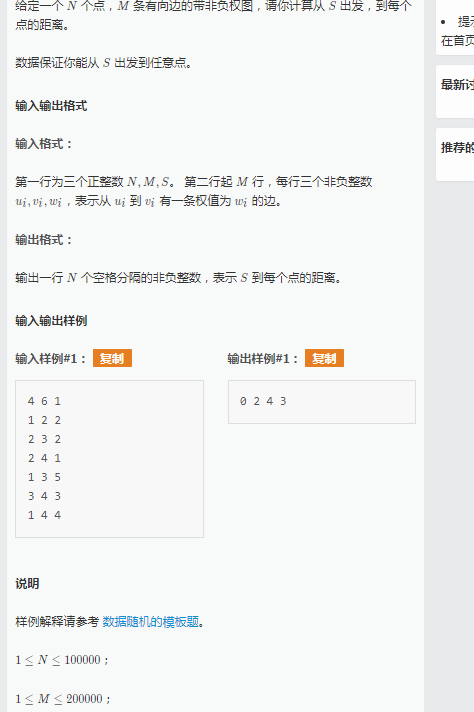
这道题spfa的玄学复杂度被卡只能过两组数据，而m，n的这个范围又不是太友好所以考虑用dijkstra加堆优化，这样就可以过了。。。

make_pari照常如此。将大根堆转成小根堆加个符号即可解决。

#include<iostream>
#include<iostream>
#include<cstring>
#include<string>
#include<cstdio>
#include<cmath>
#include<iomanip>
#include<algorithm>
#include<stack>
#include<ctime>
#include<vector>
#include<queue>
#include<map>
using namespace std;
priority_queue<pair<int,int> >q;
const int maxn=;
inline int read()
{
    int x=,f=;char ch=getchar();
    while(ch<''||ch>''){if(ch=='-')f=-;ch=getchar();}
    while(ch>=''&&ch<=''){x=x*+ch-'';ch=getchar();}
    return x*f;
}
int lin[maxn],ver[maxn],e[maxn],nex[maxn],len=;
void add(int x,int y,int z)
{
    ver[++len]=y;
    nex[len]=lin[x];
    lin[x]=len;
    e[len]=z;
}
int n,m,s;
int dis[maxn];
bool vis[maxn];
void dijkstra()
{
    for(int i=;i<=n;i++)
        dis[i]=;
    memset(vis,,sizeof(vis));
    dis[s]=;
    q.push(make_pair(,s));
    while(q.size()!=)
    {
        int x=q.top().second;q.pop();
        if(vis[x]==)continue;
        vis[x]=;
        for(int i=lin[x];i;i=nex[i])
        {
            int tn=ver[i];
            if(dis[x]+e[i]<dis[tn])
            {
                dis[tn]=dis[x]+e[i];
                q.push(make_pair(-dis[tn],tn));
            }
        }
    }
}
int main()
{
    //freopen("1.in","r",stdin);
    n=read();m=read();s=read();
    for(int i=;i<=m;i++)
    {
        int x,y,z;
        x=read();y=read();z=read();
        add(x,y,z);
    }
    dijkstra();
    for(int i=;i<=n;i++)
        printf("%d ",dis[i]);
    return ;
}

我本楚狂人，凤歌笑孔丘。