置换检验(Permutation Test)学习[转载]

转自：https://www.cnblogs.com/bnuvincent/p/6813785.html

http://www.bioinfo-scrounger.com/archives/564

1.思想

显著性检验通常可以告诉我们一个观测值是否是有效的，例如检测两组样本均值差异的假设检验可以告诉我们这两组样本的均值是否相等（或者那个均值更大）。

我们在实验中经常会因为各种问题（时间、经费、人力、物力）得到一些小样本结果，如果我们想知道这些小样本结果的总体是什么样子的，就需要用到置换检验。

Permutation test 置换检验是Fisher于20世纪30年代提出的一种基于大量计算（computationally intensive），利用样本数据的全（或随机）排列，进行统计推断的方法，因其对总体分布自由，应用较为广泛，特别适用于总体分布未知的小样本资料，以及某些难以用常规方法分析资料的假设检验问题。在具体使用上它和Bootstrap Methods类似，通过对样本进行顺序上的置换，重新计算统计检验量（可以是均值，但也不一定选择这个统计量），构造经验分布，然后在此基础上求出P-value进行推断。

关键词：小样本、显著性检验、统计量

我们一般平时较为常用的检验要属有参检验，但是其要求样本必须满足近似正态，无离群点，数据量大等要求；而有些时候其实很难都满足以上前提条件，则这时需要使用无参检验，其只关注数据的秩，但是无参检验有时也无法处理一些样本数较少的情况，这时则可以使用置换检验。

2.例子

下面通过一个简单例子来介绍Permutation test的思想。

假设我们设计了一个实验来验证加入某种生长素后拟南芥的侧根数量会明显增加。A组是加入某种生长素后，拟南芥的侧根数量；B是不加生长素时，拟南芥的侧根数量（均为假定值）。

A组侧根数量（共12个数据）：24 43 58 67 61 44 67 49 59 52 62 50

B组侧根数量（共16个数据）：42 43 65 26 33 41 19 54 42 20 17 60 37 42 55 28

我们来用假设检验的方法来判断生长素是否起作用。我们的零假设为：加入的生长素不会促进拟南芥的根系发育。在这个检验中，若零假设成立，那么A组数据的分布和B组数据的分布是一样的，也就是服从同个分布。

接下来构造检验统计量——A组侧根数目的均值同B组侧根数目的均值之差。

statistic:= mean(Xa)-mean(Xb)

对于观测值有 Sobs:=mean(Xa)-mean(Xb)=(24+43+58+67+61+44+67+49+59+52+62+50)/12-(42+43+65+26+33+41+19+54+42+20+17+60+37+42+55+28)/16=14

我们可以通过Sobs在置换分布（permutation distribution）中的位置来得到它的P-value。

Permutation test的具体步骤是：

1.将A、B两组数据合并到一个集合中，从中挑选出12个作为A组的数据（X'a），剩下的作为B组的数据（X'b）。

Gourp:=24 43 58 67 61 44 67 49 59 52 62 50 42 43 65 26 33 41 19 54 42 20 17 60 37 42 55 28

挑选出 X'a:=43 17 44 62 60 26 28 61 50 43 33 19

X'b:=55 41 42 65 59 24 54 52 42 49 37 67 67 20 42 58

2.计算并记录第一步中A组同B组的均值之差。Sper:=mean(X'a)-mean(X'b)= -7.875

3.对前两步重复999次（重复次数越多，得到的背景分布越”稳定“）

这样我们得到有999个置换排列求得的999个Sper结果，这999个Sper结果能代表拟南芥小样本实验的抽样总体情况。

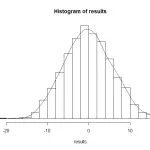
如上图所示，我们的观测值 Sobs=14 在抽样总体右尾附近，说明在零假设条件下这个数值是很少出现的。在permutation得到的抽样总体中大于14的数值有9个，所以估计的P-value是9/999=0.01

最后还可以进一步精确P-value结果（做一个抽样总体校正），在抽样总体中加入一个远大于观测值 Sobs=14的样本，最终的P-value=(9+1)/(999+1)=0.01。（为什么这样做是一个校正呢？自己思考:)）

结果表明我们的原假设不成立，加入生长素起到了促使拟南芥的根系发育的作用。

//也就是说，通过抽样，几率很小的事件发生了，是个事实，那么也就是小概率事件发生了，那么就可以推翻原假设。

3.大数、中心极限定理

大数定理：

当样本量足够多时，样本发生的频率近似于概率。

中心极限定理：　　

中心极限定理以严格的数学形式阐明了在大样本条件下，不论总体的分布如何，样本的均值总是近似地服从正态分布。

如果一个随机变量能够分解为独立同分布的随机变量序列之和，则可以直接利用中心极限定理进行解决。总之，恰当地使用中心极限定理解决实际问题有着极其重要意义。

//我好像第一次这么明白中心极限定理是什么。