HDU 1176：免费馅饼（DP，自认为很详细的解释）

免费馅饼

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)

Total Submission(s): 62694    Accepted Submission(s): 21961

Problem Description

都说天上不会掉馅饼，但有一天gameboy正走在回家的小径上，忽然天上掉下大把大把的馅饼。说来gameboy的人品实在是太好了，这馅饼别处都不掉，就掉落在他身旁的10米范围内。馅饼如果掉在了地上当然就不能吃了，所以gameboy马上卸下身上的背包去接。但由于小径两侧都不能站人，所以他只能在小径上接。由于gameboy平时老呆在房间里玩游戏，虽然在游戏中是个身手敏捷的高手，但在现实中运动神经特别迟钝，每秒种只有在移动不超过一米的范围内接住坠落的馅饼。现在给这条小径如图标上坐标：

为了使问题简化，假设在接下来的一段时间里，馅饼都掉落在0-10这11个位置。开始时gameboy站在5这个位置，因此在第一秒，他只能接到4,5,6这三个位置中其中一个位置上的馅饼。问gameboy最多可能接到多少个馅饼？（假设他的背包可以容纳无穷多个馅饼）

Input

输入数据有多组。每组数据的第一行为以正整数n(0<n<100000)，表示有n个馅饼掉在这条小径上。在结下来的n行中，每行有两个整数x,T(0<T<100000),表示在第T秒有一个馅饼掉在x点上。同一秒钟在同一点上可能掉下多个馅饼。n=0时输入结束。

Output

每一组输入数据对应一行输出。输出一个整数m，表示gameboy最多可能接到m个馅饼。

提示：本题的输入数据量比较大，建议用scanf读入，用cin可能会超时。
Sample Input

6

5 1

4 1

6 1

7 2

7 2

8 3

0

Sample Output

4

思路

找出输入的最大时间，从最大时间下开始向前找能接到的最多的馅饼数。最后输出时间为0，位置为5的馅饼数。

状态转移方程：dp[i][j]=max(dp[i+1][j+1],max(dp[i+1][j],dp[i+1][j-1]))

实现过程：

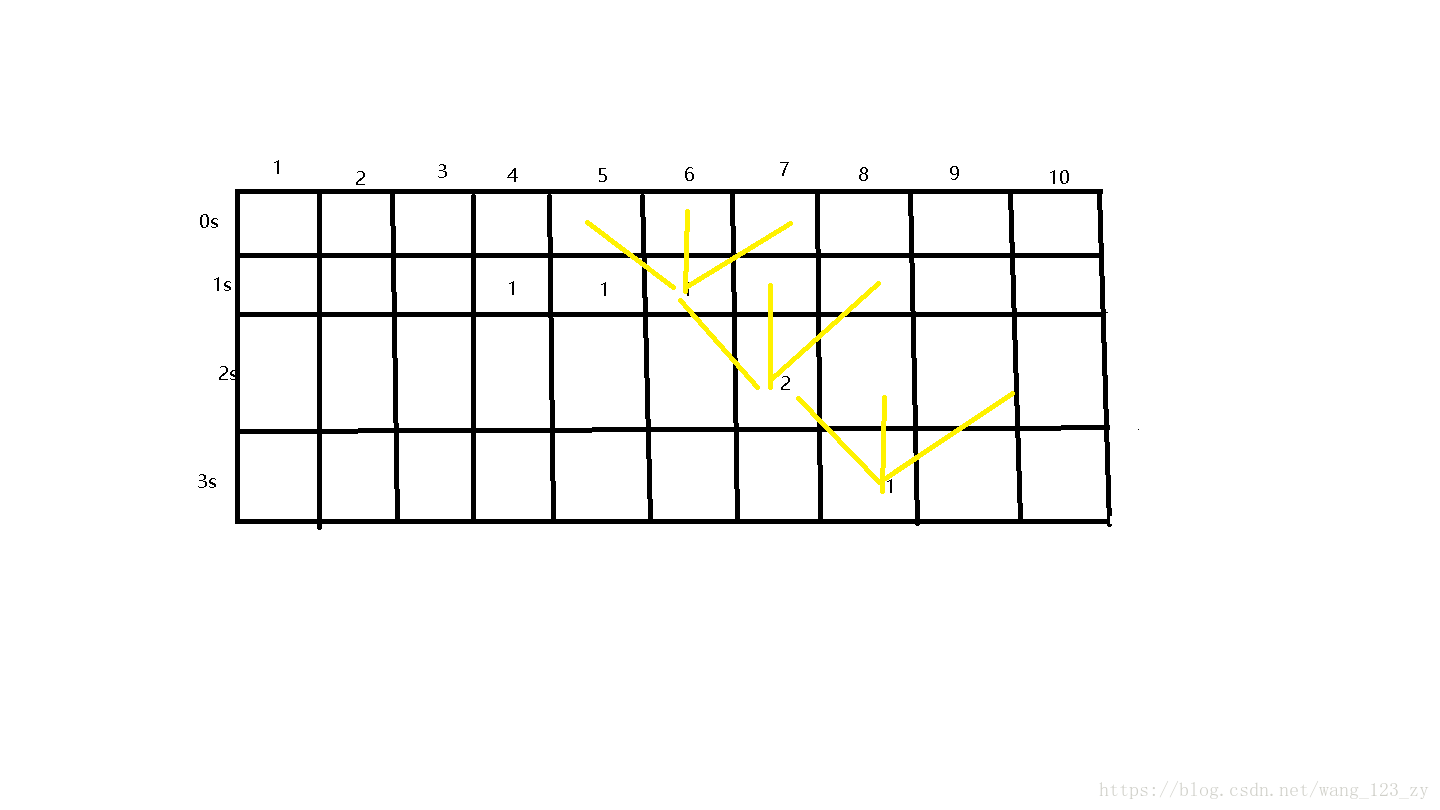
该题样例可以建立成一个二维矩阵，如图所示

那么从最后一行开始，因为每个点在每秒有三种可能走的情况，所以要记录下走到某点时拿到馅饼数的最大值。每次dp[i][j]都会在本身的基础上加上dp[i+1][j+1],dp[i+1][j],dp[i+1][j-1]这三者的最大值

如：在开始的时候，dp[3][8]=1,dp[2][7]=2 。在状态转移后，倒数第二行的元素变成了

0

0

0

0

0

0

3

1

1

0

继续往前走，倒数第三行（第1s的那一行）各元素变成了

0

0

0

1

1

4

3

3

0

0

到第一行（第0s）

0

0

1

1

4

4

4

3

3

0

这时候输出起始位置dp[0][5]的值就可以了

AC代码

#include <stdio.h>
#include <string.h>
#include <iostream>
#include <algorithm>
#include <math.h>
#include <limits.h>
#include <map>
#include <stack>
#include <queue>
#include <vector>
#include <set>
#include <string>
#define ll long long
#define ms(a) memset(a,0,sizeof(a))
#define pi acos(-1.0)
#define INF 0x3f3f3f3f
const double E=exp(1);
const int maxn=1e5+10;
using namespace std;
int dp[maxn][20];
int main(int argc, char const *argv[])
{
	// 状态转移方程：dp[i]=max(dp[i+1][j+1],max(dp[i+1][j-1],dp[i+1][j]))
	int n;
	while(~scanf("%d",&n)&&n)
	{
		ms(dp);
		int res=0;
		int place,time;
		for(int i=0;i<n;i++)
		{
			scanf("%d%d",&place,&time);
			dp[time][place]++;
			res=max(res,time);
		}
		for(int i=res;i>=0;i--)
		{
			for(int j=0;j<11;j++)
			{
				dp[i][j]+=max(dp[i+1][j-1],max(dp[i+1][j+1],dp[i+1][j]));
			}
		}
		printf("%d\n",dp[0][5]);
	}
	return 0;
}