POJ 3321 Apple Tree (DFS + 树状数组)

题意：

一棵苹果树有N个分叉，编号1---N（根的编号为1），每个分叉只能有一颗苹果或者没有苹果。 现在有两种操作：

1.某个分叉上的苹果从有变无或者从无边有。

2.需要统计以某个分叉为根节点时，它的子树上（包括该分叉）共有多少苹果。

分析： 有两种操作，基本就是使用数据结构维护的题目了。开始想了很久，不懂如何将分叉转化为一维线性的树状数组维护。 看了下discuss，有人说了时间戳三字。想了想，发现如果按照节点遍历的顺序可以制造出时间上的线性关系。 例如：

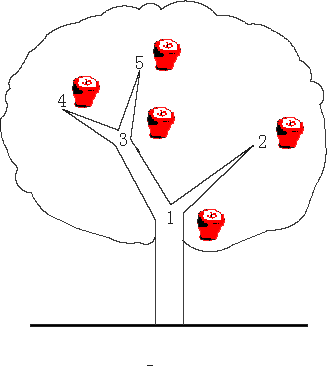
连接情况为：1---->2     1--->3    3--->4        3--->5

以1为根节点开始dfs，则遍历到每个点的时间可以为       1---->1     3--->2    4--->3    5---->4     2--->5

用两个数组begin，end统计以节点i为根时，遍历的第一个点的时间，和遍历最后一个点的时间

所以：begin[1] = 1 ;  end[1] = 5;   begin[2] = 5 ; end[2] = 5;   begin[3] = 2; end[3] = 4;........................................................

改变节点i的状态，时间戳小于i的会受影响；求和时，只需求(begin[i],end[i])的和了............................这样就变成了单点更新，区间求和的问题了。

#include <iostream>
#include <algorithm>
#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <string>
#include <vector>
#include <set>
#include <queue>
#include <stack>
#include <climits>//形如INT_MAX一类的
#define MAX 100005
#define INF 0x7FFFFFFF
#define REP(i,s,t) for(int i=(s);i<=(t);++i)
#define ll long long
#define mem(a,b) memset(a,b,sizeof(a))
#define mp(a,b) make_pair(a,b)
#define L(x) x<<1
#define R(x) x<<1|1
# define eps 1e-5
//#pragma comment(linker, "/STACK:36777216") ///传说中的外挂
using namespace std;

int begin[MAX],end[MAX],cnt[MAX],vis[MAX];
int c[MAX];
int n,m,step;
char op;
struct node {
    int s,e,next;
} ed[MAX];
int head[MAX],num;

void init() {
    memset(head,-1,sizeof(head));
    num = 0;
    step = 1;
    memset(c,0,sizeof(c));
    memset(cnt,1,sizeof(cnt));
    memset(vis,0,sizeof(vis));
}

void addedge(int s,int e) {
    ed[num].s = s;
    ed[num].e = e;
    ed[num].next = head[s];
    head[s] = num ++;
}

int lowbit(int x) {
    return x & (-x);
}

void update(int x,int va) {
    while(x > 0) {
        c[x] += va;
        x -= lowbit(x);
    }
}

int query(int x) {
    int sum = 0;
    while(x <= n) {
        sum += c[x];
        x += lowbit(x);
    }
    return sum;
}

void dfs(int v0) {
    vis[v0] = 1;
    begin[v0] = step;
    for(int i=head[v0]; i != -1; i = ed[i].next) {
        int e = ed[i].e;
        if(vis[e] == 0) {
            step ++;
            dfs(e);
        }
    }
    end[v0] = step;
}

int main() {
    init();
    scanf("%d",&n);
    int x,y;
    for(int i=0; i<n-1; i++) {
        scanf("%d%d",&x,&y);
        addedge(x,y);
    }
    dfs(1);
    for(int i=1; i<=n; i++) update(i,1);
    scanf("%d",&m);
    for(int i=0; i<m; i++) {
        getchar();
        scanf("%c%d",&op,&x);
        if(op == 'Q') {
            printf("%d\n",query(begin[x]) - query(end[x] + 1));
        }
        if(op == 'C') {
            cnt[x] ++;
            if(cnt[x] % 2 == 0) update(begin[x],-1);
            else update(begin[x],1);
        }
    }
    return 0;
}