hdu 1978 How many ways(记忆化搜索)

这是一个简单的生存游戏，你控制一个机器人从一个棋盘的起始点(1,1)走到棋盘的终点(n,m)。游戏的规则描述如下：
1.机器人一开始在棋盘的起始点并有起始点所标有的能量。
2.机器人只能向右或者向下走，并且每走一步消耗一单位能量。
3.机器人不能在原地停留。
4.当机器人选择了一条可行路径后，当他走到这条路径的终点时，他将只有终点所标记的能量。

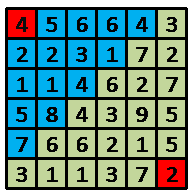
如上图，机器人一开始在(1,1)点，并拥有4单位能量，蓝色方块表示他所能到达的点，如果他在这次路径选择中选择的终点是(2,4)

点，当他到达(2,4)点时将拥有1单位的能量，并开始下一次路径选择，直到到达(6,6)点。
我们的问题是机器人有多少种方式从起点走到终点。这可能是一个很大的数，输出的结果对10000取模。

 

Input

第一行输入一个整数T,表示数据的组数。
对于每一组数据第一行输入两个整数n,m(1 <= n,m <= 100)。表示棋盘的大小。接下来输入n行,每行m个整数e(0 <= e < 20)。

 

Output

对于每一组数据输出方式总数对10000取模的结果.

 

Sample Input

1

6 6

4 5 6 6 4 3

2 2 3 1 7 2

1 1 4 6 2 7

5 8 4 3 9 5

7 6 6 2 1 5

3 1 1 3 7 2

 

Sample Output

3948

 

思路：既然dp可以，记忆化搜素同样也是可行的，把终点的可行方案置1即可

#include <cstdio>
#include <map>
#include <iostream>
#include<cstring>
#include<bits/stdc++.h>
#define ll long long int
#define M 6
using namespace std;
inline ll gcd(ll a,ll b){return b?gcd(b,a%b):a;}
inline ll lcm(ll a,ll b){return a/gcd(a,b)*b;}
int moth[]={,,,,,,,,,,,,};
int dir[][]={, ,, ,-, ,,-};
int dirs[][]={, ,, ,-, ,,-, -,- ,-, ,,- ,,};
const int inf=0x3f3f3f3f;
const ll mod=1e9+;
int n,m;
int G[][];
int dp[][];
int dfs(int x,int y){
    int mm=;
    if(dp[x][y]) return dp[x][y];
    int t=G[x][y];
    for(int i=;i<=t;i++)
        for(int j=;j<=t;j++){
            if(i+j==) continue;
            if(i+j>t) break;
            int xx=x+i;
            int yy=y+j;
            if(xx<=n&&yy<=m){
                mm=(mm+dfs(xx,yy))%;
            }

        }
    return dp[x][y]=mm;
}
int main(){
    ios::sync_with_stdio(false);
    int t;
    cin>>t;
    while(t--){
        cin>>n>>m;
        memset(dp,,sizeof(dp));
        for(int i=;i<=n;i++)
            for(int j=;j<=m;j++)
                cin>>G[i][j];
        dp[n][m]=;
        dfs(,);
        cout<<dp[][]%<<endl;
    }
    return ;
}