luogu p1652 圆

题目部分

题目描述

给出N个圆,保证任意两个圆都相离，然后给出两个点（x1,y1）、（x2,y2），保证均不在某个圆上，要从点（x1,y1）到（x2,y2）画条曲线，问这条曲线最少穿过多少次圆的边界？

输入输出格式

输入格式：

第一行为一个整数N，表示圆的个数；

第二行是N个整数，表示N个圆的X坐标；

第三行是N个整数，表示N个圆的Y坐标；

第四行是N个整数，表示N个圆的半径R；

第五行是四个整数x1,y1,x2,y2.

【数据规模】

1≤N≤50，坐标范围[-1000,1000]，每个圆的半径1<=R<=1000。

保证没有两个圆有公共点，起点和终点不会落到某个圆的边界上。

输出格式：

仅一个整数，表示最少要穿过多少次圆的边界。

输入输出样例

输入样例#1：

7
1 -3 2 5 -4 12 12
1 -1 2 5 5 1 1
8 1 2 1 1 1 2
-5 1 12 1

输出样例#1：

3

分析

所以，这题真的是。。。太厉害了

分析No.1(Wrong)

一开始以为只有四种情况：如图

1

2

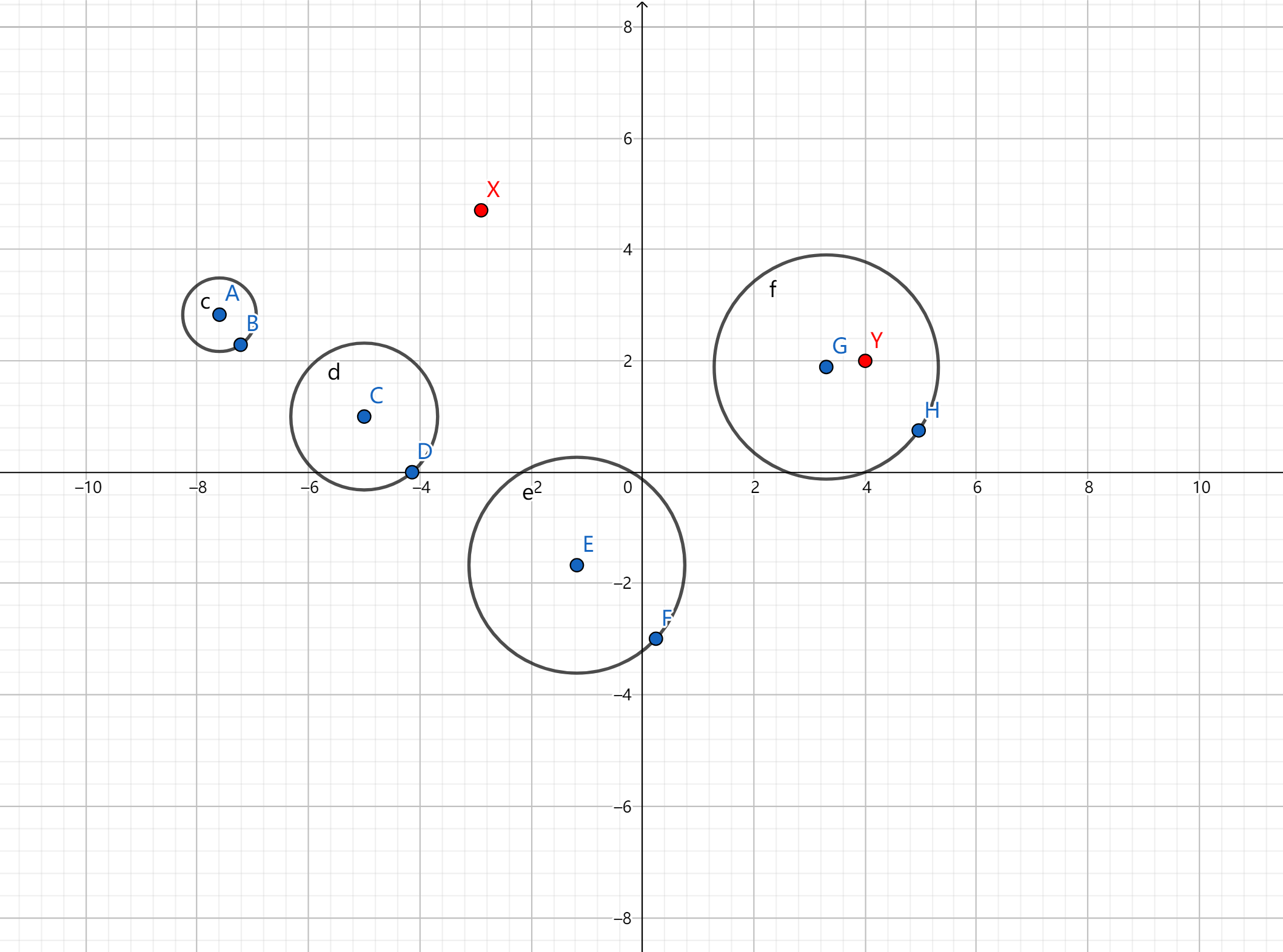
3

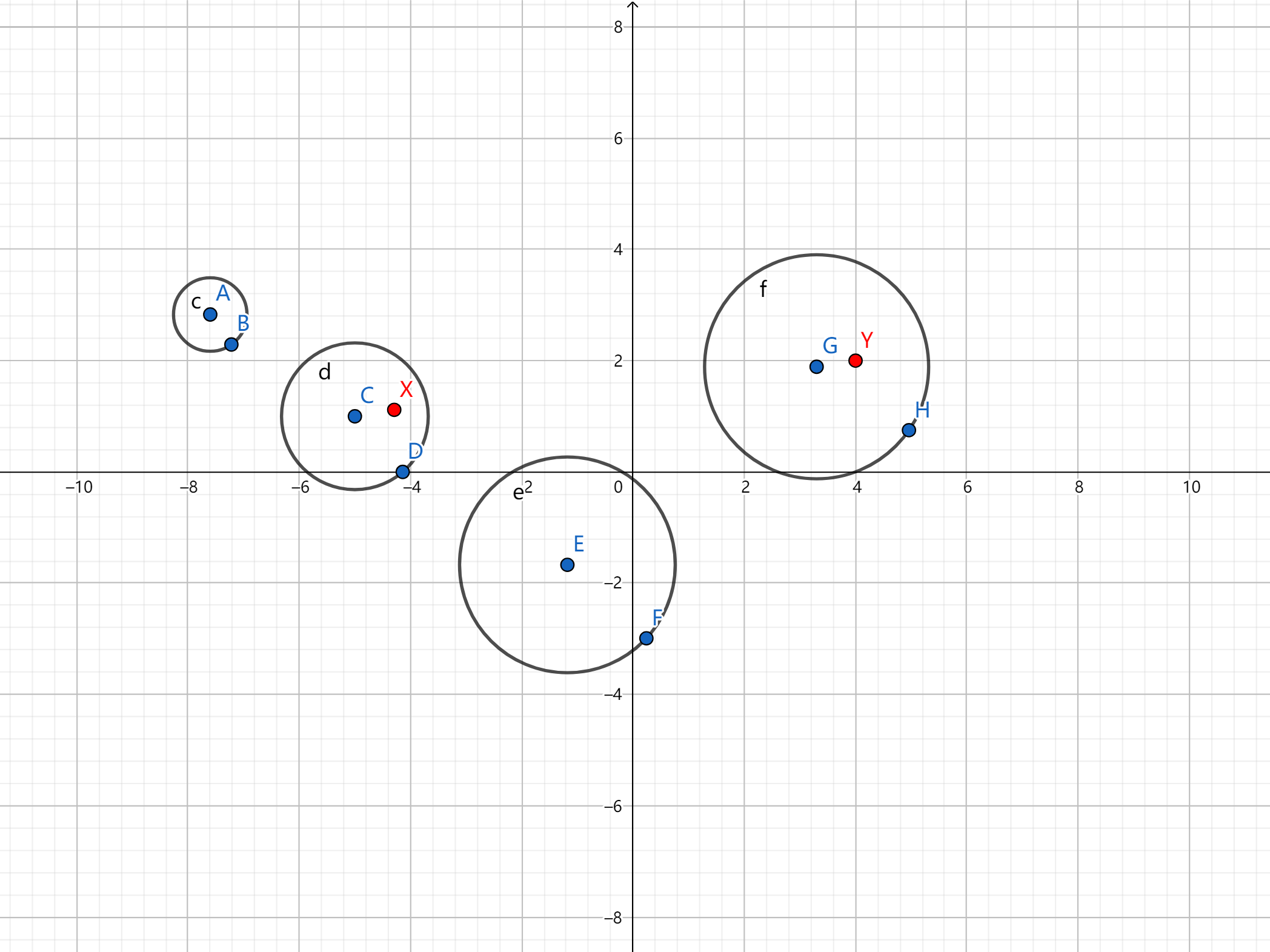
4

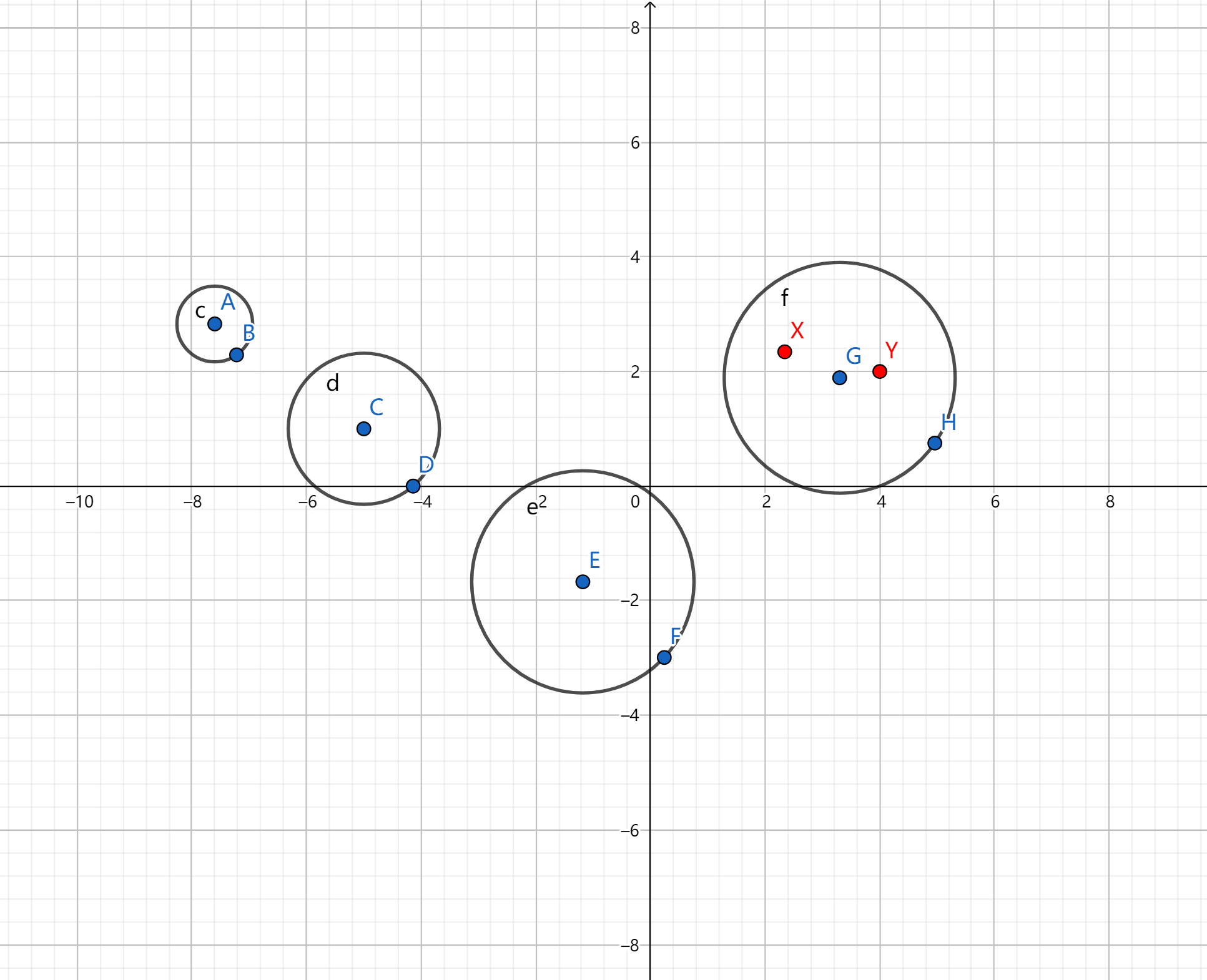
所以

所以，只有三种答案：0，1，2

然而我发现：

对了：就是，有3？！！！！

mmpmmpmmpmmp

既然这样，我就生气了，所以

分析No.2

画图

我把样例画了一下，然后发现。。。

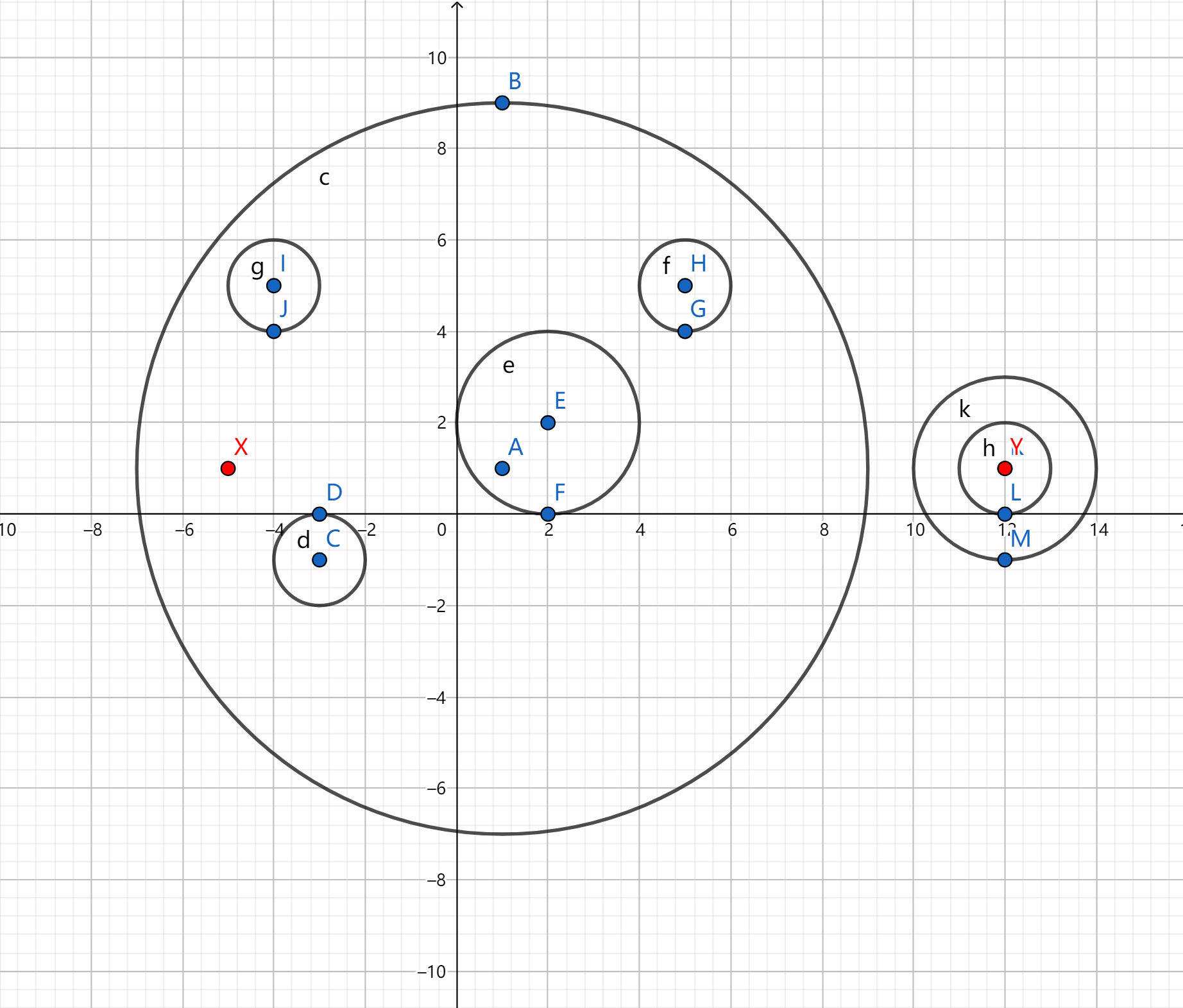
发现

他所谓的相离, 包含内含！！！！

那就明了了，我说怎么会有3。。。

代码

#include<cstdio>
#include<iostream>
#include<cmath>
using namespace std;
int x[60],y[60];
double r[60];
int x1,yy,x2,y2;//这里不知道为什么用有y1会报错。。。可能是我没学到那种东西。。。
bool f1,f2;
int ans;
int main()
{
  int n;
  scanf("%d",&n);
  for(int i=1;i<=n;i++) scanf("%d",&x[i]);
  for(int i=1;i<=n;i++) scanf("%d",&y[i]);
  for(int i=1;i<=n;i++) scanf("%lf",&r[i]);
  scanf("%d%d%d%d",&x1,&yy,&x2,&y2);
  for(int i=1;i<=n;i++)
  {
    double tmp1=sqrt(((x1-x[i])*(x1-x[i]))+((yy-y[i])*(yy-y[i])));
    double tmp2=sqrt(((x2-x[i])*(x2-x[i]))+((y2-y[i])*(y2-y[i])));
    if(tmp1<r[i]!=tmp2<r[i]) ans++;//如果那两个给定的点都在同一圆内，就不用再加一次相交了
  }
  cout<<ans<<endl;
  return 0;
}

好了我记住了，分析样例，分析样例，分析样例！！！！！