逻辑回归 代价函数J关于系数theta求导
J=-y*loga-(1-y)*log(1-a)
梯度下降,求dJ/d_theta_j
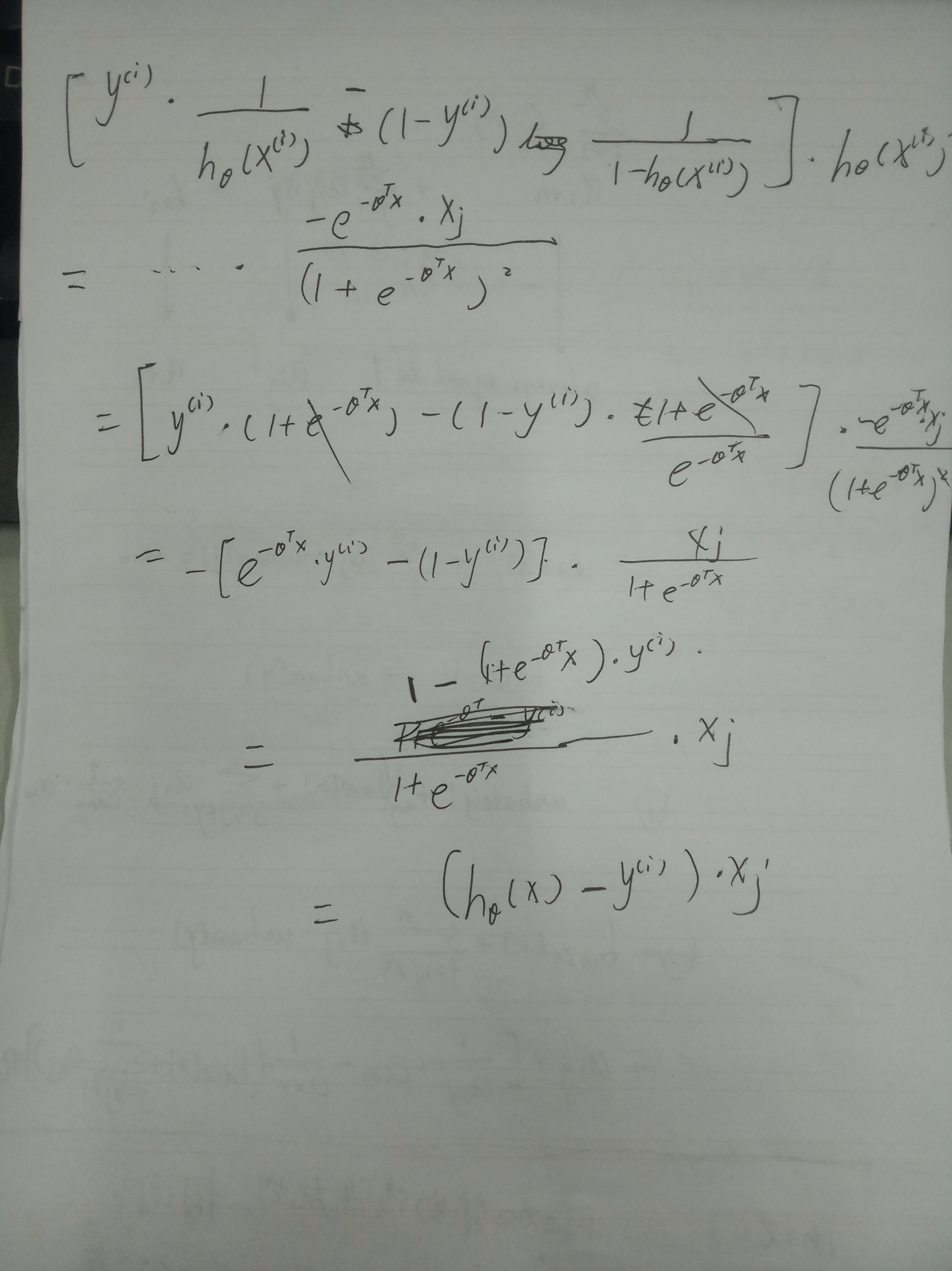
逻辑回归 代价函数J关于系数theta求导的更多相关文章
- Machine Learning--week3 逻辑回归函数(分类)、决策边界、逻辑回归代价函数、多分类与(逻辑回归和线性回归的)正则化
Classification It's not a good idea to use linear regression for classification problem. We can use ...
- Logistic Regression(逻辑回归)
分类是机器学习的一个基本问题, 基本原则就是将某个待分类的事情根据其不同特征划分为两类. Email: 垃圾邮件/正常邮件 肿瘤: 良性/恶性 蔬菜: 有机/普通 对于分类问题, 其结果 y∈{0,1 ...
- ML 逻辑回归 Logistic Regression
逻辑回归 Logistic Regression 1 分类 Classification 首先我们来看看使用线性回归来解决分类会出现的问题.下图中,我们加入了一个训练集,产生的新的假设函数使得我们进行 ...
- DeepLearning之路(一)逻辑回归
逻辑回归 1. 总述 逻辑回归来源于回归分析,用来解决分类问题,即预测值变为较少数量的离散值. 2. 基本概念 回归分析(Regression Analysis):存在一堆观测资料,希望获得数据内 ...
- 斯坦福第六课:逻辑回归(Logistic Regression)
6.1 分类问题 6.2 假说表示 6.3 判定边界 6.4 代价函数 6.5 简化的成本函数和梯度下降 6.6 高级优化 6.7 多类分类:一个对所有 6.1 分类问题 在分类问题中 ...
- 大叔学ML第五:逻辑回归
目录 基本形式 代价函数 用梯度下降法求\(\vec\theta\) 扩展 基本形式 逻辑回归是最常用的分类模型,在线性回归基础之上扩展而来,是一种广义线性回归.下面举例说明什么是逻辑回归:假设我们有 ...
- [C2] 逻辑回归(Logistic Regression)
逻辑回归(Logistic Regression) 假设函数(Hypothesis Function) \(h_\theta(x)=g(\theta^Tx)=g(z)=\frac{1}{1+e^{-z ...
- 逻辑回归模型(Logistic Regression, LR)--分类
逻辑回归(Logistic Regression, LR)模型其实仅在线性回归的基础上,套用了一个逻辑函数,但也就由于这个逻辑函数,使得逻辑回归模型成为了机器学习领域一颗耀眼的明星,更是计算广告学的核 ...
- 逻辑回归原理,推导,sklearn应用
目录 逻辑回归原理,推导,及sklearn中的使用 1 从线性回归过渡到逻辑回归 2 逻辑回归的损失函数 2.1 逻辑回归损失函数的推导 2.2 梯度下降法 2.3 正则化 3 用逻辑回归进行多分类 ...
随机推荐
- Field tTypeMapper in com.atguigu.project.service.imp.projectInfoServiceImpl required a bean of type 'com.atguigu.project.mapper.TTypeMapper' that could not be found.
解决:MapperScan
- SQL 给视图赋权限
授予表权限 创建视图 授予视图权限 测试权限 复杂程度: 初级 数据要求: 使用自备的数据 您可以使用 SQL 在企业级地理数据库中创建表和要素类的视图. 本主题中的示例显示如何使用 Microsof ...
- Windows Server2008、IIS7启用CA认证及证书制作完整过程
1 添加活动目录证书服务 1.1 打开服务器管理器,右键点击角色,选择“添加角色”,在“添加角色向导”窗口左侧面板选择“服务器角色”,然后勾选“Active Dire ...
- Qt 使用openGL 渲染NV12格式的视频
直接上代码 Nv12Render.h #ifndef NV12RENDER_H #define NV12RENDER_H #include <QOpenGLFunctions> #incl ...
- 检测某一目录下md5相同的文件
import org.apache.commons.codec.digest.DigestUtils; import org.apache.commons.io.IOUtils; import jav ...
- Ubuntu开发用新机安装流程
1.SSH安装 Ubuntu缺省已安装客户端,此处安装服务端 sudo apt-get install openssh-server 确认sshserver是否启动 netstat -tlp | gr ...
- 大学jsp实验6session
1.session对象的使用 (1)设计一个简单的在线问卷调查程序,共有3个页面,分别是one.jsp.two.jsp.three.jsp. 其中,shiyan6_1_one.jsp页面效果如下图所示 ...
- subprocess 模块
import subprocess # 就用来执行系统命令 import os cmd = r'dir D:\上海python全栈4期\day23 | findstr "py"' ...
- VIM 光标移动常用命令
h或^h 向左移一个字符 k或^p 向上移一行 j或^j或^n 向下移一行 l或空格 向右移一个字符 G 移到文件的最后一行 nG 移到文件的第n行 w 移到下一个字的开头 W 移到下一个字 ...
- vi编辑光标跳到文件开头和结尾以及清空文件命令
vi编辑光标跳到文件开头和结尾以及清空文件命令 按esc退出编辑模式 跳到文件开头: :1 跳到文件结尾: :$ 清空文件内容: 小写的 d 加上大写的 G
