0基础算法基础学算法 第八弹 递归进阶，dfs第一讲

　　最近很有一段时间没有更新了，主要是因为我要去参加一个重要的考试----小升初！作为一个武汉的兢兢业业的小学生当然要去试一试我们那里最好的几个学校的考试了，总之因为很多的原因放了好久的鸽子，不过从今天开始我要回归正轨了，以后基本上都是每周更一篇（注：不是每周一篇0基础算法系列，可能是学习笔记），因为马上我也要去报道了！

-----------正文分割线------------

　　·之前我早就在第六弹就讲述过关于递归的内容（https://www.cnblogs.com/qj-Network-Box/p/12729230.html）今天我们要讲的dfs便是递归的一种拓展应用，dfs中文全名叫做深度优先搜索，至于什么是深度优先搜索其实也不好解释，所以我们可以在例题中弄明白，dfs的原理就是利用递归的特性，函数套函数，层层递进，越搜越深，这也是它名字的来历，现在我们可以开始我们的第一个示例

一，有1 2 3三个数字卡片放进a b c三个盒子里，有哪些排列组合方法

　　这道题有好几种做法，比较常规的做法是枚举各种情况，比较简单易懂，循环就完了嘛，循环三次，枚举三个数，每次都枚举1-3的数字卡片，分别装入a b c的盒子里，代码如下

 #include <bits/stdc++.h>
 using namespace std;
 int main(){
     int k=;//第三个数
     for(int i=;i<=;i++)
     for(int j=;j<=;j++)//筛前两个数
     {
         if(j!=i)
         {
             while(k==i||k==j)//筛第三个数
             {
                 k++;
                 k=k%+;//免得k出现大于等于4的情况
             }
             cout<<i<<" "<<j<<" "<<k<<endl;//输出
         }
     }
     return ;
 } 

运行结果也很明了

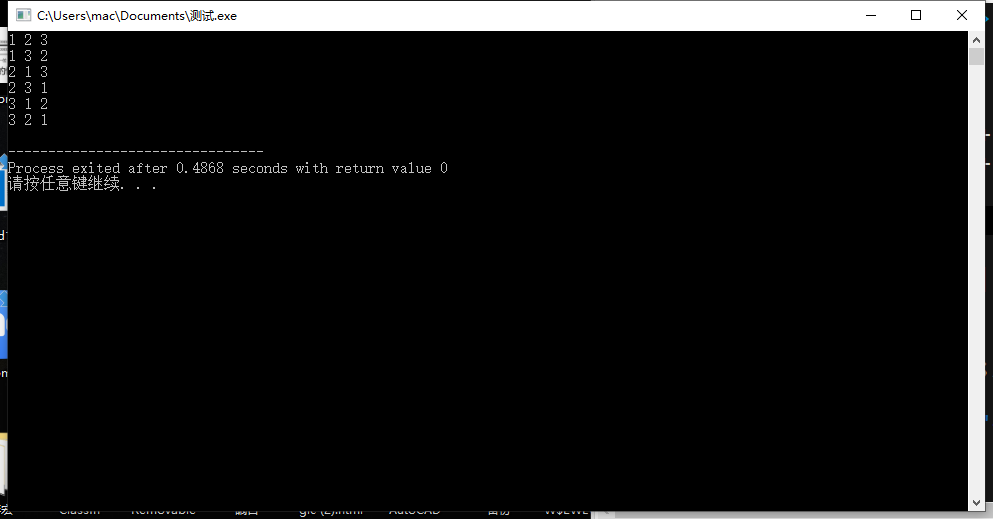
可以看到最后一共六种结果，分别是123 132 213 231 312和321；

这样做当然是可以轻易做出来，但要是不只是有三个球三个盒子呢，如果是100000个球，100000个盒子呢，那就得写100000个循环了，同时if语句也是少不了的，这样一写得写到猴年马月啊，因此这肯定是不可能的，这时候就得请出搜索家族中的dfs，深度优先搜索了

一，dfs解“有1 2 3三个数字卡片放进a b c三个盒子里，有哪些排列组合方法”

　　写搜索前非常重要的一个步骤是要提前理好思路，如果不太清楚如何整理思路，可以看看我的第一弹(https://www.cnblogs.com/qj-Network-Box/p/12502643.html),按照我的习惯我一般会画一个流程图理清思路，如下图

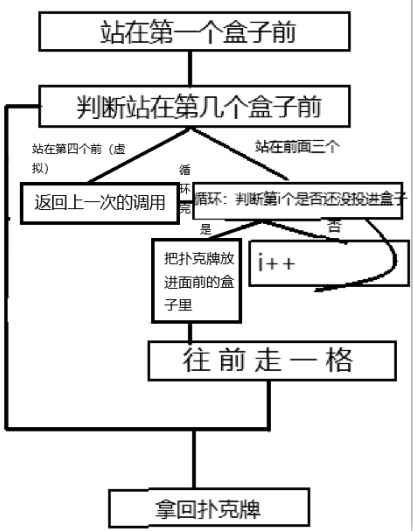
流程图可以帮我们理好思路，接下来是我们的代码部分

#include <bits/stdc++.h>
using namespace std;
int a[];
int b[];//a是盒子，b是卡片,true表示在手上，false表示不再
void dfs(int k)
{
    if(k==)//如果他站在了“第四个”盒子前
    {
        for(int i=;i<=;i++) cout<<a[i]<<" ";
        cout<<endl;
        return;//返回上一步
    }
    for(int i=;i<=;i++)
    {
        if(b[i]==)
        {
            a[k]=i;//在a[k]的盒子中装入扑克牌i
            b[i]=;//b[i]的卡片已经放在盒子里的
            dfs(k+);//递归继续搜下一个盒子
            b[i]=;//卡片记得拿回来，搜索剩下的组合时还要用的
        }
    }
 }
int main(){
    dfs();//直接调用
    return ;
} 

运行结果完全正确

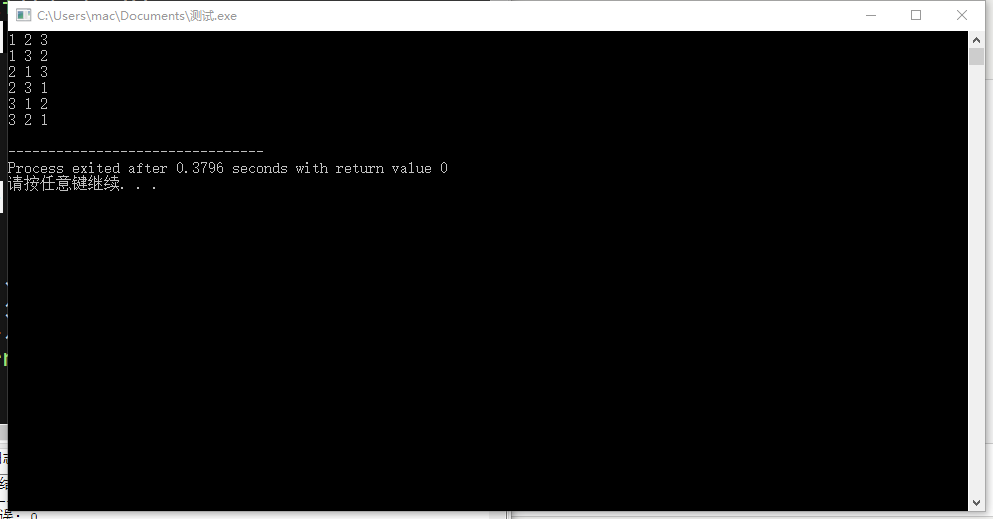
结果完全正确

看到这里，很多人会感到很不解，明明套几个循环就可以解决的东西，为什么要这样大费周章地整那么麻烦的递归呢？这道题我们的目的并不是把他真的做出来，而是为了引入这样的概念，况且就像我前面说的，这只是三个数三个盒子，如果是100000个数，100000个盒子呢？那样就只能选择使用dfs的方法了，接下来我再给大家看一道”简单“的题（不太熟练者慎入，这个题大概还要等2-3弹后才会涉及的难度）

二，洛谷题单 八皇后

#include<bits/stdc++.h>
using namespace std;
int n, a[], sum;
bool book[][];
void dfs(int i)
{
    int j;
    if(i>n)
    {
        sum++;
        if(sum>) return ;
        for(int i=;i<=n;i++)    cout<<a[i]<<" ";
        cout<<endl;
        return ;
    }

    for(j=;j<=n;j++)
        if( !book[][j] && (!book[][i+j]) && (!book[][i-j+n]) )
    {
        a[i] = j;
        book[][j] = ;
        book[][i+j] = ;
        book[][i-j+n] = ;
        dfs(i+);
        book[][j] = ;
        book[][i+j] = ;
        book[][i-j+n] = ;
    }
}

int main()
{
    cin>>n;
    dfs();
    cout<<sum;
    return ;
}

上面是一种解决方式的代码，用的就是dfs，但是里面涉及了一些后两弹会说的一些pmn的内容，到那时候我会以八皇后为例题讲解，关注了我后敬请期待吧！

　　第八弹 dfs第一讲算是结束了，以后还有第九弹 dfs2，第十弹 dfs3，如果觉得我讲的还不错，就麻烦您动动手指，点赞关注，如果您没有cnblogs的账号，也可以加入QQ群，群号1031457671，或者使用链接加入群聊 https://jq.qq.com/?_wv=1027&k=poupnxU3，群里有丰富资源、电子书，同时也欢迎大家进群交流分享自己的电子书，欢迎各位进群！