字符串学习总结（Hash & Manacher & KMP）

前言

终于开始学习新的东西了，总结一下字符串的一些知识。

NO.1 字符串哈希（Hash）

定义

即将一个字符串转化成一个整数，并保证字符串不同,得到的哈希值不同，这样就可以用来判断一个该字串是否重复出现过。

所以说\(Hash\)就是用来求字符串是否相同或者包含的。（包含关系就可以枚举区间，但是通常用\(KMP\)，不会真的有人用看脸的\(Hash\)做字符串匹配吧，不会吧不会吧)。

实现

实现方式也是比较简单的，其实就是把一个字符串转化为数字进行比较，到这里可能有人就会说，直接比较长度和\(ASCII\)码不就行了，也是转化成数字啊（放屁）。这样显然是不行的，就好比说"ab"和“ba“，这两个显然不一样，但是如果按上边说的进行比较就是一样的，这样就错了，所以我们要换一种方式：改变一下进制。

如果是一个纯字符串的话，那么我们应该把进制调到大于\(131\)，因为如果小于，就不能给每一种的字符一个值，那么正确性也就无法保证了。所以取一个\(233\)，合情合理，还很sao（逃。因为这个值至少能保证不会炸。我们求出来每个字符串对应的数字，然后进行比较就好了。

对于哈希而言，我们认为对一个数取模后一样，那么就是一样的，所以可以偷点懒，也就是自然溢出，使用\(unsigned\ long\ long\)，相当于自动对\(2^{64}\)取模，然后进行比较即可，当然，可以自己背一个\(10^{18}\)的质数进行取模（毕竟也是能卡的，也不知道哪个毒瘤会卡），各有优缺点。

代码

ull Hash(char s[]){//ull自然溢出
	ull res = 0;
	int len = strlen(s);
	for(int i=0;i<len;++i){//计算每一位，用自己定义的进制base乘（也就是233 qwq）
		res = (res*base + (ull)s[i])%mod;//这里我是取了个玄学mod
	}
	return res;
}

以上就是整个字符串之间的对比。下边说一说字符串里某个区间的对比

区间对比

意思就是直接给出你几个字符串，对比每个字符串里给定的区间\([l,r]\)，这样的话如果直接一个个的扫，肯定会慢好多，如果直接求整个串然后相减，那么肯定是错误的，因为每一位都是要乘以一个进制的，如果直接计算，那么肯定就会乱掉，也就\(WA\)了。所以要用到之前说的东东：前缀和。

我们记录每一位的前缀和，而记算的时候需要乘以当前位的进制，这样就会避免上边说到的那种迷惑错误。记录的时候就照常按照前缀和记录，只需要最后改一下判断就行。

定义\(pw[len]\)为长度为\(len\)时的需要乘以的进制，前缀和就用\(sum\)来表示，求前缀和就是这样：

int main(){
	cin>>s;
	int len = strlen(s);
	sum[0] = (ull)s[0];
	for(int i=1;i<len;++i){
		sum[i] = sum[i-1]*base+(ull)a[i];//乘以进制不能忘
	}
}

下边是判断是否合法：

	while(n--){
		int l,r,s,t,len;
		cin>>l>>r>>s>>t;
		len = r-l+1;//计算第几位来乘以进制，pw数组提前可以快速幂处理好
		if(sum[r] - sum[l-1]*pw[len] == sum[t]-sum[s-1]*pw[len])printf("YES\n");//如果这样计算出来值相等就合法
		else printf("NO\n");
	}

模板例题

字符串哈希

例题代码

#include<bits/stdc++.h>
using namespace std;
#define ull unsigned long long
const ull mod = 1926081719260817;
const int maxn = 1e4+10;
ull base = 233;
int a[maxn];
char s[maxn];
ull Hash(char s[]){
	ull res = 0;
	int len = strlen(s);
	for(int i=0;i<len;++i){
		res = (res*base + (ull)s[i])%mod;
	}
	return res;
}
int main(){
	int n;
	scanf("%d",&n);
	for(int i=1;i<=n;++i){
		cin>>s;
		a[i] = Hash(s);
	}
	int ans = 1;
	sort(a+1,a+n+1);
	for(int i=1;i<n;++i){
		if(a[i] != a[i+1])ans++;
	}
	printf("%d\n",ans);
}

NO.2 Manacher算法

学长说很不常用，所以理解一个思想即可。

定义

\(1975\)年，\(Manacher\)发明了\(Manacher\)算法（中文名：马拉车算法），是一个可以在\(O(n)\)的复杂度中返回字符串\(s\)中最长回文子串长度的算法，十分巧妙。

例如这个字符串：“abaca”，它可以处理每一位的回文字串，以\(O(n)\)的效率处理最大值（当然还是有扩展的，只不过它不太常用，就只是分析一下算法过程）

实现

因为回文串分为奇回文串和偶回文串，处理起来比较麻烦，所以我们要用到一个小（sao）技（cao）巧（zuo），在每两个字符之间插入一个不会出现的字符，但是要求插入的字符一样，这样才能保证不影响回文串的长度。

举个例子：“abbadcacda”这个字符串，我们需要插入新的字符，这里用’#'，那么就有了如下对应关系：

其中定义\(p[i]\)为以\(i\)为半径的回文半径，也就是从中心向两边最长能拓展多少，而根据这个可以推出来以它为中心的真正的回文串的长度。也就是\(p[i]-1\)，根据这个就可以得到最长的回文串的长度了。

但是复杂度为什么是\(O(n)\)呢，那么就涉及到了他的实现方法，我们定义一个回文中心\(C\)和这个回文的右侧\(R\)，也就是当前中心的最长回文的右端点，如果枚举到的\(i\)大于\(R\)，那么直接更新就行，但是如果在里边，那么会分出来三种情况：

\(1\)、枚举到的\(i\)关于\(C\)对称到\(i'\)，这时候\(i'\)的回文区域在\([L,R]\)，那么\(i\)的回文半径就是\(i'\):

证明：因为此时的\([L,R]\)就是一个回文区间，所以左右对称过来是一样的，所以得到\(i\)的回文半径。

\(2\)、枚举到\(i\)，此时对称点\(i'\)的回文区域超出了\(L\)，那么\(i\)的回文区域就一定是从\(i\)到\(R\)。

证明：借用一张图片便于解释：

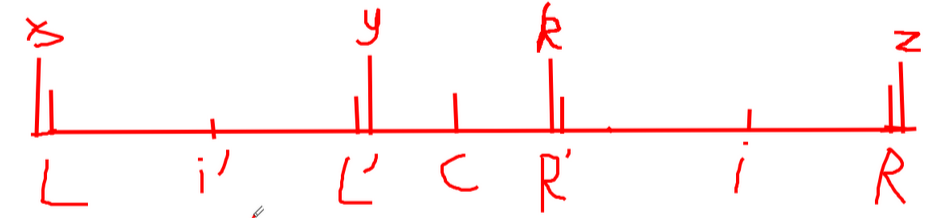
（图好丑……）首先我们设\(L\)点关于\(i'\)对称的点为\(L'\)，\(R\)点关于\(i\)点对称的点为\(R'\)，\(L\)的前一个字符为\(x\)，\(L’\)的后一个字符为\(y\)，\(k\)和\(z\)同理，此时我们知道\(L - L'\)是\(i'\)回文区域内的一段回文串，故可知\(R’ - R\)也是回文串，因为\(L - R\)是一个大回文串。所以我们得到了一系列关系，\(x = y，y = k，x != z\)，所以 \(k != z\)。这样就可以验证出\(i\)点的回文半径是\(i - R\)。

\(3\)、\(i'\) 的回文区域左边界恰好和\(L\)重合，此时\(i\)的回文半径最少是\(i\)到\(R\)，回文区域从\(R\)继续向外部匹配。

证明：因为 \(i'\) 的回文左边界和L重合，所以已知的\(i\)的回文半径就和\(i'\)的一样了，我们设\(i\)的回文区域右边界的下一个字符是\(y\)，\(i\)的回文区域左边界的上一个字符是\(x\)，现在我们只需要从\(x\)和\(y\)的位置开始暴力匹配，看是否能把\(i\)的回文区域扩大即可。

小小总结一下，其实就是先进行暴力匹配，然后根据\(i'\)回文区域和左边界的关系进行查找。

例题+代码

Manacher板子

#include<bits/stdc++.h>
using namespace std;
const int maxn = 11e6;
char s[maxn];
int Manacher(char s[]){
	int len = strlen(s);
	if(len == 0)return 0;//长度为0就return
	int len1 = len * 2 + 1;
	char *ch = new char[len1];//动态数组
	int *par = new int[len1];
	int head = 0;
	for(int i=0;i<len1;++i){
		ch[i] = (i & 1) == 0 ? '#' : s[head++];//插入不一样的字符
	}
	int C = -1;
	int R = -1;
	int Max = 0;
	par[0] = 1;
	for(int i=0;i<len1;++i){//枚举三种情况
		par[i] = (i < R)? min(par[C*2-i],R-i) : 1;//取最小的回文半径
		while(i + par[i] < len1 && i - par[i] > -1&& ch[i + par[i]] == ch[i - par[i]]){//暴力匹配
			par[i] ++ ;
		}
		if(i + par[i] > R){//如果超过右边界就更新
		 	R = i + par[i];
			C = i;
		}
		Max = max(Max,par[i]);//更新最大半径
	}
	delete[] ch;//清空动态数组
	delete[] par;
	return Max - 1;//因为这个是添了字符的最大回文半径，所以回文串的最长是它-1
}
int main(){
	cin>>s;
	cout<<Manacher(s);
	return 0;
}

NO.3 KMP算法

正常我们查找字符串是否为子串的时候，往往都是暴力枚举，效率为\(O(n^2)\)，但是字符串长了或者多了，肯定就是不行的了，所以有了\(KMP\)算法。

定义

\(KMP\)算法是一种改进的字符串匹配算法，由\(D.E.Knuth，J.H.Morris\)和\(V.R.Pratt\)同时发现，因此人们称它为克努特——莫里斯——普拉特操作（简称\(KMP\)算法）。\(KMP\)算法的关键是利用匹配失败后的信息，尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是实现一个\(next\)函数，函数本身包含了模式串的局部匹配信息。时间复杂度\(O(m+n)\)。

通俗的来说就是在需要匹配的那个串上给每个位置一个失配指针\(fail[j]\)，表示在当前位置\(j\)失配的时候需要返回到\(fail[j]\)位置继续匹配，而这就是\(KMP\)算法优秀复杂度的核心。

实现

失配数组的匹配就是把需要查找的那个字符串进行一遍前缀和后缀之间的匹配。我们举个例子"ababa"这里真前缀分别为"a","ab","aba","abab"，真后缀为"a","ba","aba","baba",找到他们的最大相同位置，就是\(fail\)指针，

我们设\(kmp[i]\) 用于记录当匹配到模式串的第 \(i\) 位之后失配,该跳转到模式串的哪个位置，那么对于模式串的第一位和第二位而言，只能回跳到 \(1\)，因为是 \(KMP\)是要将真前缀跳跃到与它相同的真后缀上去（通常也可以反着理解），所以当 \(i=0\) 或者 \(i=1\) 时,相同的真前缀只会是 \(str1(0)\)这一个字符，所以\(kmp[0]=kmp[1]=1\)。

模板+代码

KMP字符串匹配

#include<bits/stdc++.h>
using namespace std;
const int maxn = 1e6+10;
char a[maxn],b[maxn];
int kmp[maxn];
int main(){
	cin>>a+1>>b+1;
	int lena = strlen(a+1);
	int lenb = strlen(b+1);
	int j = 0;
	for(int i=2;i<=lenb;++i){//自己跟自己匹配处理出kmp数组
		while(j && b[i] != b[j+1]){
			j = kmp[j];
		}
		if(b[i] == b[j+1])j++;
		kmp[i] = j;
	}
	j = 0;
	for(int i=1;i<=lena;++i){
		while(j && a[i] != b[j+1]){
			j = kmp[j];
		}
		if(a[i] == b[j+1])j++;
		if(j == lenb){//匹配完了就输出位置
			printf("%d\n",i-lenb+1);
			j = kmp[j];//返回失配位置
		}
	}
	for(int i=1;i<=lenb;++i){
		printf("%d ",kmp[i]);
	}
	return 0;
}