Codeforces Edu Round 49 A-E

A. Palindromic Twist

由于必须改变。所以要使\(a[i] = a[n - i + 1]\)。

要么同向走，但必须满足之前的\(a[i] = a[n - i + 1]\)。

要么相遇，必须满足两字符相差\(2\)的距离。

#include <cstdio>
#include <iostream>
#include <cmath>
using namespace std;
const int N = 110;
int n;
char str[N];
bool judge(){
    for(int i = 1; i <= n / 2; i++)
        if(abs(str[i] - str[n - i + 1]) != 2 && abs(str[i] - str[n - i + 1]) != 0) return false;
    return true;
}
int main(){
    int T; scanf("%d", &T);
    while(T--){
        scanf("%d%s", &n, str + 1);
        if(judge()) puts("YES");
        else puts("NO");
    }
    return 0;
}

B. Numbers on the Chessboard

找规律题，如果\(n\)是奇数，则每行有可能\((n - 1) / 2\) 或 \((n + 1) / 2\)个数字，可以分治考虑：

#include <iostream>
#include <cstdio>
#define int long long
using namespace std;
int n, q;
signed main(){
    scanf("%lld%lld", &n, &q);
    for(int i = 1; i <= q; i++){
        int x, y; scanf("%lld%lld", &x, &y);
        int num = 0;
        if(n % 2){
            if((x + y) % 2 == 0){
                if(x % 2) num = (x - 1) * n / 2 + y / 2 + 1;
                else num = (x - 2 + 1) * n / 2 + 1 + y / 2;
            }else{
                if(x % 2) num = n * n / 2 + 1 + (x - 1) * n / 2 + y / 2;
                else num = n * n / 2 + (x - 2 + 1) * n / 2 + 1 + y / 2 + 1;
            }
        }else{
            if((x + y) % 2 == 0){
                if(x % 2) num = (x - 1) * (n / 2) + y / 2 + 1;
                else num = (x - 1) * (n / 2) + y / 2;
            }else{
                if(x % 2) num = n * n / 2 + (x - 1) * (n / 2) + y / 2;
                else num = n * n / 2 + (x - 1) * (n / 2) + y / 2 + 1;
            }
        }
        printf("%lld\n", num);

    }
    return 0;
}

C. Minimum Value Rectangle

设矩形的两边长为\(a\)、\(b\)，且\(a <= b\)，则：

\(\frac{P ^ 2}{S} = \frac{(2(a + b)) ^ 2}{a * b}= \frac{4a ^ 2 + 4b ^ 2 + 8ab }{a * b} = 4(\frac{a}{b} + \frac{b}{a}) + 8\)

使\(\frac{a}{b} + \frac{b}{a}\) 最小，只需使\(\frac{b}{a}\)最小既可，因为\(\frac{b}{a} >= 1\)，但\(\frac{a}{b} <= 1\)，故后者对总和没有影响。

#include <iostream>
#include <cstdio>
#include <limits.h>
#include <cstring>
#include <algorithm>
using namespace std;
const int SIZE = 10010;
int n, a, cnt[SIZE], d[SIZE << 1], tot, ansA, ansB;
double c, minn;

int main(){
    int T; scanf("%d", &T);
    while(T--){
        memset(cnt, 0, sizeof cnt);
        bool success = false; tot = 0;
        minn = 10001;
        scanf("%d", &n);
        for(int i = 1; i <= n; i++) {
            scanf("%d", &a), cnt[a]++;
            if(cnt[a] == 2) d[++tot] = a;
            if(cnt[a] == 4) d[++tot] = a;
        }
        sort(d + 1, d + 1 + tot);
        for(int i = 1; i < tot; i++){
            if(d[i] == d[i + 1]){ ansA = d[i], ansB = d[i + 1]; break; }
            c = (double)d[i + 1] / d[i];
            if(c < minn)ansA = d[i], ansB = d[i + 1], minn = c;
        }
        printf("%d %d %d %d\n", ansA, ansA, ansB, ansB);
    }
    return 0;
}

D. Mouse Hunt

对于每个联通块，选择环中（包括子环）的一个位置设置捕鼠夹既可。

在符合条件的位置上取最小值的和即为答案。

若选择多个点，可证明其代价要大于选一个点。

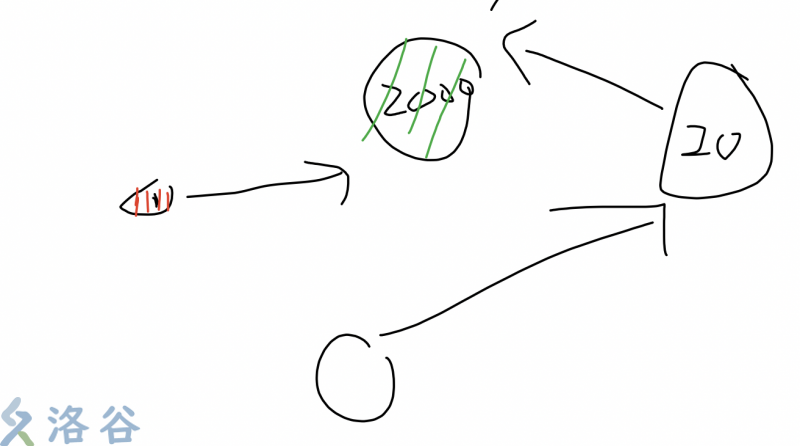
若不选择绿点，选择1 + 20，但为了保证每个房间都能干掉老鼠，所以2000是必选的，所以选择联通快中多个点的花销 > 只选一个点。

#include <iostream>
#include <cstdio>
#include <vector>
#include <limits.h>
using namespace std;
const int N = 200010;
int n, c[N], a[N], ans;
bool st[N], vis[N];
vector<int> G[N], edge, val;

void dfs(int u){
    if(vis[u]){
        val.push_back(u);
        while(edge.size() && edge.back() != u)
            val.push_back(edge.back()), edge.pop_back();
        return ;
    }
    vis[u] = true, edge.push_back(u), dfs(a[u]);
}
void mark(int u){
    for(int i = 0; i < G[u].size(); i++){
        int v = G[u][i];
        if(!st[v]) st[v] = true, mark(v);
    }
}
int main(){
    scanf("%d", &n);
    for(int i = 1; i <= n; i++) scanf("%d", c + i);
    for(int i = 1; i <= n; i++) {
        scanf("%d", a + i);
        G[i].push_back(a[i]);
        G[a[i]].push_back(i);
    }
    for(int i = 1 ; i <= n; i++){
        if(!st[i]){
            val.clear(); edge.clear();
            dfs(i);
            int res = INT_MAX;
            for(int i = 0; i < val.size(); i++)
                res = min(res, c[val[i]]);
            ans += res;
            st[i] = true, mark(i);
        }
    }
    printf("%d", ans);
    return 0;
}

E. Inverse Coloring

自闭，看了题解之后稍微理解了一点点。

设\(f[i][j][k]\) 为长度为\(i\)， 最长连续填色数为\(k\)， 尾部最长连续涂色数最长为\(j\)的方案数

可以想到，这个状态可以延展到的状态有：

• 当新结尾颜色保持跟之前一样，\(f[i + 1][j + 1][max(j + 1, k)]\)
• 不一样，\(f[i + 1][1][max(1, k)]\)

\(cnt[i]\) 实际上是长度为\(i\)的所有方案数，那么只要符合：

\(i * j < k\)，\(cnt[i] * cnt[j]\)就能被加入答案

…...

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
using namespace std;
const int N = 510, mod = 998244353;
typedef long long LL;
int n, k, f[2][N][N], cnt[N];
void update(int &a, int b){ a = (a + b) % mod; }
int main(){
    scanf("%d%d", &n, &k);
    f[0][0][0] = 1;
    for(int i = 0; i < n; i++){
        int pre = i & 1, now = pre ^ 1;
        memset(f[now], 0, sizeof f[now]);
        for(int j = 0; j <= n; j++){
            for(int k = 0; k <= n; k++){
                update(f[now][j + 1][max(j + 1, k)], f[pre][j][k]);
                update(f[now][1][max(1, k)], f[pre][j][k]);
            }
        }
    }
    for(int i = 0; i <= n; i++){
        for(int j = 0; j <= n; j++){
            update(cnt[i], f[n & 1][j][i]);
        }
    }
    LL ans = 0;
    for(int i = 1; i <= n; i++){
        for(int j = 1; j <= n; j++){
            if(i * j < k)
                ans = (ans + (LL)cnt[i] * cnt[j]) % mod;
        }
    }
    printf("%lld", (ans / 2) % mod);
    return 0;
}