Java数据结构——AVL树

AVL树(平衡二叉树)定义
　　AVL树本质上是一颗二叉查找树，但是它又具有以下特点：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树，并且拥有自平衡机制。在AVL树中任何节点的两个子树的高度最大差别为一，所以它也被称为平衡二叉树。下面是平衡二叉树和非平衡二叉树对比的例图：

　　平衡因子(bf)：结点的左子树的深度减去右子树的深度，那么显然-1<=bf<=1;

AVL树的作用
　　我们知道，对于一般的二叉搜索树（Binary Search Tree），其期望高度（即为一棵平衡树时）为log2n，其各操作的时间复杂度（O(log2n)）同时也由此而决定。但是，在某些极端的情况下（如在插入的序列是有序的时），二叉搜索树将退化成近似链或链，此时，其操作的时间复杂度将退化成线性的，即O(n)。我们可以通过随机化建立二叉搜索树来尽量的避免这种情况，但是在进行了多次的操作之后，由于在删除时，我们总是选择将待删除节点的后继代替它本身，这样就会造成总是右边的节点数目减少，以至于树向左偏沉。这同时也会造成树的平衡性受到破坏，提高它的操作的时间复杂度。
　　例如：我们按顺序将一组数据1,2,3,4,5,6分别插入到一颗空二叉查找树和AVL树中，插入的结果如下图：

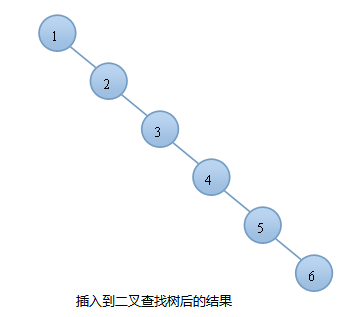
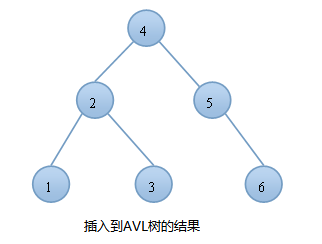
由上图可知，同样的结点，由于插入方式不同导致树的高度也有所不同。特别是在带插入结点个数很多且正序的情况下，会导致二叉树的高度是O(N)，而AVL树就不会出现这种情况，树的高度始终是O(lgN).高度越小，对树的一些基本操作的时间复杂度就会越小。这也就是我们引入AVL树的原因。

AVL树的基本操作
　　AVL树不仅是一颗二叉查找树，它还有其他的性质。如果我们按照一般的二叉查找树的插入方式可能会破坏AVL树的平衡性。同理，在删除的时候也有可能会破坏树的平衡性，所以我们要做一些特殊的处理，包括：单旋转和双旋转！
　　单旋转---右旋：

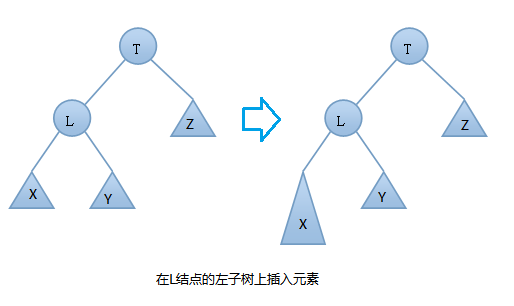
　　由上图可知：在插入之前树是一颗AVL树，而插入之后结点T的左右子树高度差的绝对值不再 < 1,此时AVL树的平衡性被破坏，我们要对其进行旋转。由上图可知我们是在结点T的左结点的左子树上做了插入元素的操作，我们称这种情况为左左情况，我们应该进行右旋转(只需旋转一次，故是单旋转)。具体旋转步骤是：
　　T向右旋转成为L的右结点，同时，Y放到T的左孩子上。这样即可得到一颗新的AVL树，旋转过程图如下：

　　单旋转---左旋：
　

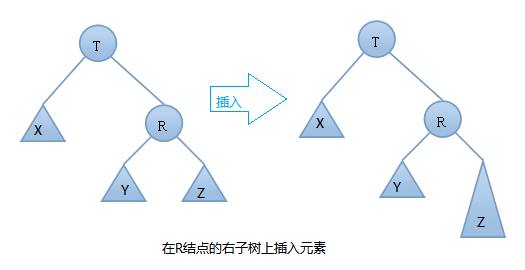
　　　由上图可知：在插入之前树是一颗AVL树，而插入之后结点T的左右子树高度差的绝对值不再 < 1,此时AVL树的平衡性被破坏，我们要对其进行旋转。由上图可知我们是在结点T的右结点的右子树上做了插入元素的操作，我们称这种情况为右右情况，我们应该进行左旋转(只需旋转一次，故事单旋转)。具体旋转步骤是：
　　　T向右旋转成为R的左结点，同时，Y放到T的左孩子上。这样即可得到一颗新的AVL树，旋转过程图如下：
　

　　以上就是插入操作时的单旋转情况！我们要注意的是：谁是T谁是L，谁是R还有谁是X,Y,Z!T始终是开始不平衡的左右子树的根节点。显然L是T的左结点，R是T的右节点。X、Y、Y是子树当然也可以为NULL.NULL归NULL，但不能破坏插入时我上面所说的左左情况或者右右情况。
　　双旋转的---左右(先左后右)旋：

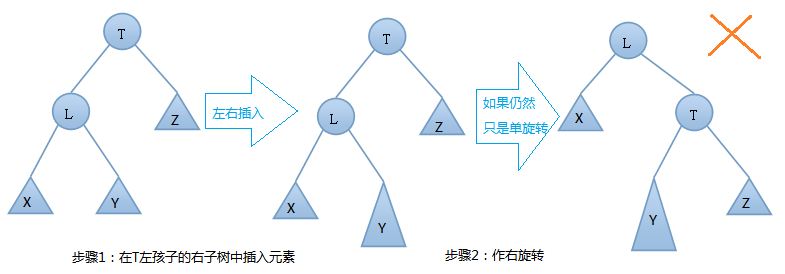
由上图可知，我们在T结点的左结点的右子树上插入一个元素时，会使得根为T的树的左右子树高度差的绝对值不再 < 1，如果只是进行简单的右旋，得到的树仍然是不平衡的。我们应该按照如下图所示进行二次旋转：
　　

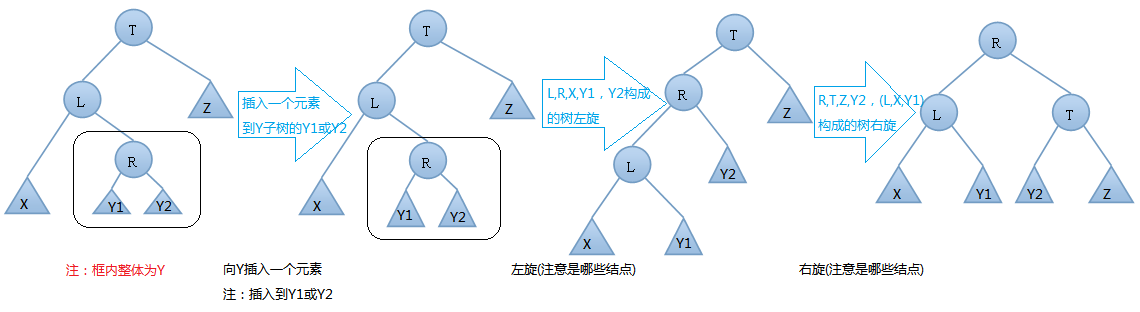
　　双旋转的---右左(先右后左)旋：

　　由上图可知，我们在T结点的右结点的左子树上插入一个元素时，会使得根为T的树的左右子树高度差的绝对值不再 < 1，如果只是进行简单的左旋，得到的树仍然是不平衡的。我们应该按照如下图所示进行二次旋转：　

简单实现

TreeNode.java

public class TreeNode {
private int data;
private TreeNode leftChild;
private TreeNode rightChild;
private int height;

public int getData() {
return data;
}

public void setData(int data) {
this.data = data;
}

public TreeNode getLeftChild() {
return leftChild;
}

public void setLeftChild(TreeNode leftChild) {
this.leftChild = leftChild;
}

public TreeNode getRightChild() {
return rightChild;
}

public void setRightChild(TreeNode rightChild) {
this.rightChild = rightChild;
}

public TreeNode(int data) {
super();
this.data = data;
//初始化话高度为1
height = 1;
}
}

　　

AVLTree.java：

import java.util.ArrayList;

public class AVLTree {
private static TreeNode root;
private static boolean flag=true;
// 获得高度
private int getHeight(TreeNode node) {
if (node == null) {
return 0;
} else {
return node.height;
}
}
// 获得节点的平衡因子
private int getBalanceFactor(TreeNode node) {
if (node == null) {
return 0;
} else {
return getHeight(node.leftChild) - getHeight(node.rightChild);
}
}
// 判断该二叉树是否是一颗二叉搜索树
public boolean isBST() {
ArrayList<Integer> datas = new ArrayList<>();
inOrder(root, datas);
for (int i = 1; i < datas.size(); i++)
if (datas.get(i - 1) > datas.get(i))
return false;
return true;
}
// 中序遍历添加进集合
public void inOrder(TreeNode node, ArrayList<Integer> datas) {
if (node != null) {
inOrder(node.getLeftChild(), datas);
datas.add(node.data);
inOrder(node.getRightChild(), datas);
} else {
return;
}
}

public void inOrder(TreeNode node) {
if (node != null) {
inOrder(node.getLeftChild());
System.out.print(node.data + " ");
inOrder(node.getRightChild());
}
}
// 判断该二叉树是否是一颗平衡二叉树
public boolean isBalanced() {
return isBalanced(root);
}

private boolean isBalanced(TreeNode node) {
if (node == null) {
return true;
} else {
int balanceFactor = getBalanceFactor(node);
if (Math.abs(balanceFactor) > 1) {
return false;
}
return isBalanced(node.leftChild) && isBalanced(node.rightChild);
}
}

// 对节点进行向右旋转操作，返回旋转后的根节点x
//      y                   x
//     / \                 /  \
//    x  T4  向右旋转(y)   z     y
//   / \    ---------->  / \   / \
//  z  T3              T1  T2 T3 T4
// / \
//T1 T2
private TreeNode rightRotate(TreeNode y) {
TreeNode x = y.leftChild;
TreeNode T3 = x.rightChild;
// 向右旋转过程
x.rightChild = y;
y.leftChild = T3;
// 更新height
y.height = Math.max(getHeight(y.leftChild), getHeight(y.rightChild)) + 1;
x.height = Math.max(getHeight(x.leftChild), getHeight(x.rightChild)) + 1;
//依次添加进avl树时可能会有60，50，40的情况，此时如果不改变root的值，root指向60，旋转后不再是根节点，即当传进来的节点指向root时，就需要改变root节点
if (y == root) {
root = x;
}
return x;
}
// 对节点进行向左旋转操作，返回旋转后的根节点x
//   y                 x
//  / \               /  \
// T1  x  向左旋转(y) y    z
//    / \ -------> / \   / \
//   T2  z        T1 T2 T3 T4
//      / \
//     T3 T4
private TreeNode leftRotate(TreeNode y) {
TreeNode x = y.rightChild;
TreeNode T2 = x.leftChild;
// 向左旋转过程
x.leftChild = y;
y.rightChild = T2;
// 更新height
y.height = Math.max(getHeight(y.leftChild), getHeight(y.rightChild)) + 1;
x.height = Math.max(getHeight(x.leftChild), getHeight(x.rightChild)) + 1;
//依次添加进avl树时可能会有40，50，60的情况，此时如果不改变root的值，root指向40，旋转后不再是根节点，需要改变，即当传进来的节点指向root时，就需要改变root节点
if (y== root) {
root = x;
}
return x;
}
// 添加节点
public TreeNode addNode(TreeNode node, int data) {
if (root == null) {
TreeNode treeNode = new TreeNode(data);
root = treeNode;
return root;
}
if (node == null) {
TreeNode treeNode = new TreeNode(data);
return treeNode;
} else {
if (data < node.data) {
node.leftChild = addNode(node.leftChild, data);
} else if (data > node.data) {
node.rightChild = addNode(node.rightChild, data);
} else {
node.data = data;
}
// 更新height
node.height = 1 + Math.max(getHeight(node.leftChild), getHeight(node.rightChild));
// 计算平衡因子
int balanceFactor = getBalanceFactor(node);
// LL
if (balanceFactor > 1 && getBalanceFactor(node.leftChild) >= 0) {
return rightRotate(node);
}
// RR
if (balanceFactor < -1 && getBalanceFactor(node.rightChild) <= 0) {
return leftRotate(node);
}
// LR
if (balanceFactor > 1 && getBalanceFactor(node.leftChild) < 0) {
node.leftChild = leftRotate(node.leftChild);
return rightRotate(node);
}
// RL
if (balanceFactor < -1 && getBalanceFactor(node.rightChild) > 0) {
node.rightChild = rightRotate(node.rightChild);
return leftRotate(node);
}
return node;
}
}
// 删除节点
public TreeNode deleteNode(TreeNode node, int data) {
if (node == null) {
System.out.println("find not");
flag=false;
return null;
}
TreeNode retNode;
if (data < node.data) {
node.leftChild = deleteNode(node.leftChild, data);
retNode = node;
} else if (data > node.data) {
node.rightChild = deleteNode(node.rightChild, data);
retNode = node;
} else {
// 左子树为空的时候
if (node.leftChild == null) {
TreeNode rightNode = node.rightChild;
node.rightChild = null;
retNode = rightNode;
}
// 右子树为空的时候
else if (node.rightChild == null) {
TreeNode leftNode = node.leftChild;
node.leftChild = null;
retNode = leftNode;
} else {
// 左右子树都不为空的时候
// 找到待删除节点的后继节点
TreeNode successor = processer(node.rightChild);
//如果删除的恰好是根节点
if (node == root) {
root = successor;
}
successor.rightChild = deleteNode(node.rightChild, successor.data);
successor.leftChild = node.leftChild;
node.leftChild = node.rightChild = null;
retNode = successor;
}
}
if (retNode == null) {
return null;
} else {
// 更新height
retNode.height = 1 + Math.max(getHeight(retNode.leftChild), getHeight(retNode.rightChild));
// 计算平衡因子
int balanceFactor = getBalanceFactor(retNode);
// LL
if (balanceFactor > 1 && getBalanceFactor(retNode.leftChild) >= 0) {
return rightRotate(retNode);
}
// RR
if (balanceFactor < -1 && getBalanceFactor(retNode.rightChild) <= 0) {
return leftRotate(retNode);
}
// LR
if (balanceFactor > 1 && getBalanceFactor(retNode.leftChild) < 0) {
retNode.leftChild = leftRotate(retNode.leftChild);
return rightRotate(retNode);
}
// RL
if (balanceFactor < -1 && getBalanceFactor(retNode.rightChild) > 0) {
retNode.rightChild = rightRotate(retNode.rightChild);
return leftRotate(retNode);
}
return retNode;
}
}
// 寻找后继节点
private TreeNode processer(TreeNode node) {
if (node.leftChild == null) {
return node;
} else {
return processer(node.leftChild);
}
}
// 修改节点
public boolean updateNode(int oldData, int newData) {
TreeNode del = deleteNode(root, oldData);
if(flag==false) {
return false;
}else {
addNode(root, newData);
return true;
}
}
// 查找节点
public TreeNode findNode(int data) {
TreeNode current = root;
while (current.data != data) {
if (data < current.data) {
current = current.leftChild;
} else {
current = current.rightChild;
}
if (current == null) {
return null;
}
}
return current;
}

public static void main(String[] args) {
AVLTree tree = new AVLTree();
int[] arr = new int[] { 60, 50, 40, 30, 20, 10 };
//依次添加进avl树
for (int i : arr) {
tree.addNode(root, i);
}
//中序遍历
tree.inOrder(root);
System.out.println();
//是否是BST
System.out.println("is BST:" + tree.isBST());
//是否平衡
System.out.println("is Balanced:" + tree.isBalanced());
//添加节点45
tree.addNode(root, 45);
//是否还是BST
System.out.println("is BST:" + tree.isBST());
//是否还是平衡的
System.out.println("is Balanced:" + tree.isBalanced());
//查找节点50
System.out.println(tree.findNode(50));
//删除节点后
tree.deleteNode(root, 40);
//是否还是BST
System.out.println("is BST:" + tree.isBST());
//是否还是平衡的
System.out.println("is Balanced:" + tree.isBalanced());
tree.updateNode(45, 51);
//是否还是BST
System.out.println("is BST:" + tree.isBST());
//是否还是平衡的
System.out.println("is Balanced:" + tree.isBalanced());
}
}