【图像处理】使用OpenCV+Python进行图像处理入门教程（二）

这篇随笔介绍使用OpenCV进行图像处理的第二章 图像的运算，让我们踏上继续回顾OpenCV进行图像处理的奇妙之旅，不断地总结、回顾，以新的视角快速融入计算机视觉的奥秘世界。

2  图像的运算

复杂的图像处理是借助基础的图像运算来实现的，本章介绍图像运算的基本操作，为后续实现更加复杂的处理提供帮助。

2.1  图像加法运算

可以通过加法运算符“+”和cv2.add函数实现图像的加法运算，但这两种方法对数据求和后溢出255的处理方式不一样。

设a、b均为8为灰度图像，像素饱和值为255。a图像像素值为a，b图像像素值为b。

（一）加法运算符“+”

原理：取余运算：a+b = (a+b)mod(256)

语法格式：

print('a+b=\n',a+b)

该方法会使两数之和大于255时取余，两数之和小于255时不变。

（二）cv2.add()函数

语法格式：

result=cv2.add(a,b)

该方法会使两数之和大于255时置为255，两数之和小于255时不变。

在cv2.add()函数中，有下列三种用法：图像与图像加法、图像与数值加法、数值与图像加法，如：

img3=cv2.add(img1,img2)   #图像与图像加法
img3=cv2.add(img1,5)         #图像与数值加法
img3=cv2.add(7,img2)         #数值与图像加法

2.2  图像加权之和

实际图像加法过程中，可能要考虑不同图像的权重，也就是图像的加权之和。

使用cv2.addWeighted()函数实现，但需保证两幅图片大小和类型相同。

语法格式：

#alpha是img1的权重，beta是img2的权重，gamma是整体亮度调节参数，不能省略
img3=cv2.addWeighted(img1,alpha,img2,beta,gamma)

2.3  按位逻辑运算

按位逻辑运算的原理与电路中“与门”“或门”“异或门”“非门”类似，是非常重要的一种基本运算方式。

Opencv中使用如下函数进行按位逻辑运算：

cv2.bitwise_and()  #按位与，两逻辑值为真，则为真
cv2.bitwise_or()   #按位或，两逻辑值有一真，则为真
cv2.bitwise_xor()  #按位异或，两逻辑值相同为假，不同为真
cv2.bitwise_not()  #按位非，逻辑值取反

其语法格式如下：

c=cv2.bitwise_and(a,b)
c=cv2.bitwise_or(a,b)
c=cv2.bitwise_xor(a,b)
c=cv2.bitwise_not(a,b)

注1：掩模图像用于对另一幅图片中ROI区域的掩盖处理，掩模图像只有两种数值：0和255，常和另一幅图像进行按位逻辑运算。一幅图片中的数值与掩模图像中的0值按位与后，数值变为0（黑色遮盖）；与掩模图像中的255值按位与后，数值不变（原区域）。

注2：如果待处理图像为彩色，就需要将掩模图像转为BGR模式的彩色图像，如：

a=cv2.imread('tupian',1)    #读取图片
b=np.zeros(a.shape,dtype=np.uint8)   #转为BGR类型

2.4  掩模（掩码）

上一小节中提到了掩模图像的概念，举例来解释，例如：

 1 import cv2
 2 import numpy as np
 3 img1=np.ones((4,4),dtype=np.uint8)*2  #生成4×4的二维数组img1
 4 img2=np.ones((4,4),dtype=np.uint8)*6  #生成4×4的二维数组img2
 5 mask=np.zeros((4,4),dtype=np.uint8)   #生成4×4的掩模数组mask
 6 mask[1:3,1:3]=1
 7 img3=np.ones((4,4),dtype=np.uint8)*99 #生成4×4的二维数组img3
 8 print('img1=\n',img1)
 9 print('img2=\n',img2)
10 print('mask=\n',mask)
11 print('初始值img3=\n',img3)
12 img3=cv2.add(img1,img2,mask=mask)     #img3与mask进行掩模运算
13 print('求和后的img3=\n',img3)

上例所示的掩模mask值有两种，一种是空值0，一种是非空值（一般取1或255等容易按位与操作的数值）。当mask值为0的像素点，与另一像素矩阵对应位点按位与操作后，数值依然是0，相当于把这一像素矩阵构成的图片用黑布遮盖掉一部分；当mask值非空，就可以处理这些非空值对应在另一像素矩阵上的位点。

当彩色图像与掩模图像计算时，需要将掩模转换为BGR模式的三通道彩色图，继而实现掩模运算。

2.5  位平面分解

将一幅灰度图像中不同像素位点上的同一比特位二进制数组合在一起，会得到一张二进制图像，该图像称为灰度图像的一个位平面，该过程叫做位平面分解。是不是还不明白什么叫做位平面？哈哈别着急，我们看下面举例。

设一张灰度图像的像素值为：

147	206	168	243
72	198	49	126
132	77	186	62
228	157	129	28

将其转化为二进制数为：

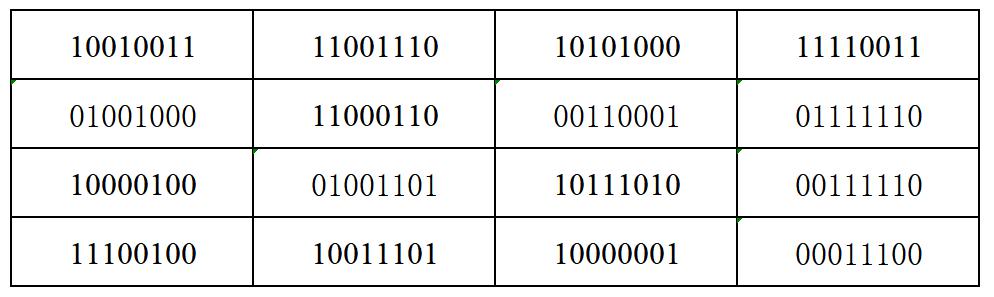
将这些像素点A_i 同一比特位点上的值组合，得到8个位平面：

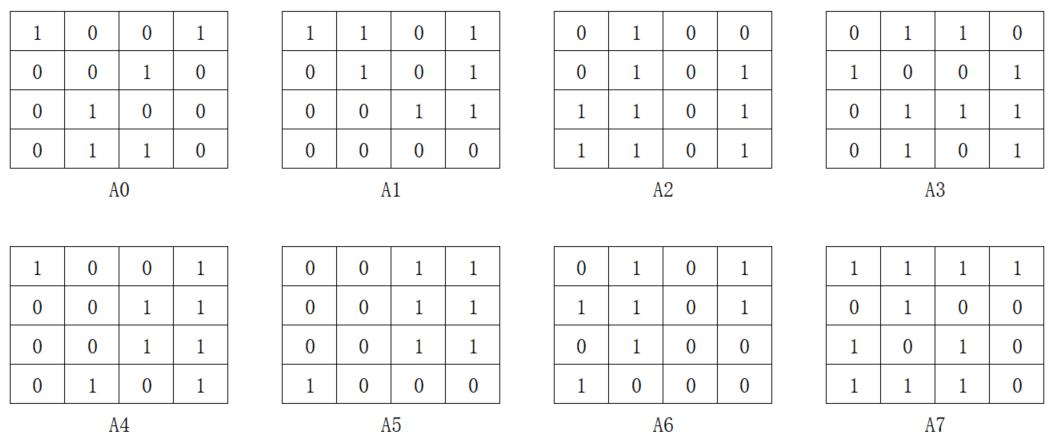
A0表示第0个位平面，依次类推。

位平面分解，有5个步骤 ：图像预处理、构造提取矩阵、提取位平面、阈值处理、显示图像。其算法实现如下例所示：

 1 import cv2
 2 import numpy as np
 3 lena=cv2.imread('E:\python_opencv\lena.jpg',0)
 4 cv2.imshow('lena',lena)
 5 r,c=lena.shape
 6 x=np.zeros((r,c,8),dtype=np.uint8)   #设置各个位平面的提取矩阵，8个通道
 7 for i in range(8):
 8     x[:,:,i]=2**i                    #设置各个位平面提取矩阵的值2**i
 9 r=np.zeros((r,c,8),dtype=np.uint8)
10 for i in range(8):
11     r[:,:,i]=cv2.bitwise_and(lena,x[:,:,i])  #原图与提取矩阵值按位与运算
12     mask=r[:,:,i]>0                  #阈值处理
13     r[mask]=255
14     cv2.imshow(str(i),r[:,:,i])
15 cv2.waitKey()
16 cv2.destroyAllWindows()

2.6  图像加密和解密

将图像与秘钥图像按位异或，能够实现图像的加密；将加密后的图像再次与秘钥图像按位异或，可以实现图像的解密。对一个像素点加密和解密的举例如下：

bit_xor(216,178)=106  #对像素点216加密
bit_xor(106,178)=216  #对像素点216解密

图像的加密和解密程序举例如下：

encryption=cv2.bitwise_xor(lena,key)  #lena与key按位异或加密
dncryption=cv2.bitwise_xor(encryption,key)  #加密图与key按位异或解密

2.7  数字水印

先介绍一个定义：最低有效位（Least Significant Bit, LSB）指一个二进制数中的第0位。

数字水印即一幅图像中的最低有效位上隐藏了信息，该信息可以是音频、视频、图像等，为了形象介绍，本节将隐藏的水印信息使用简单的二值图像表示。

实现数字水印分为两个过程：嵌入过程和提取过程。

嵌入过程：先将载体图像的像素进行二进制转化处理，然后把水印图像的像素值进行阈值处理变为1或0，最后把载体图像的最低有效位替换为二进制水印图像（按位或运算）。

提取过程：先读取嵌入水印后的图像，生成一个同样大小和类型的提取矩阵（元素值均为1），最后将嵌入水印的图像与该提取矩阵进行按位与运算。

这次内容就分享到这里了，下次继续更新第3章色彩空间的类型转换，希望与各位老师和小伙伴们交流学习~