VJ train1 O-统计问题 题解

原谅我缺少设备，只能手写图解

题目：

          在一无限大的二维平面中，我们做如下假设：
             1、  每次只能移动一格；
             2、  不能向后走（假设你的目的地是“向上”，那么你可以向左走，可以向右走，也可以向上走，但是不可以向下走）；
             3、  走过的格子立即塌陷无法再走第二次；

             求走n步不同的方案数（2种走法只要有一步不一样，即被认为是不同的方案）。

                       Input首先给出一个正整数C，表示有C组测试数据
                       接下来的C行，每行包含一个整数n (n<=20)，表示要走n步。
                        Output请编程输出走n步的不同方案总数；
                         每组的输出占一行。
                             

Sample Input

2
1
2

Sample Output

3
7

说实话，刚看到这题还是有点懵逼的，但仔细推敲一下还是能找出破绽的

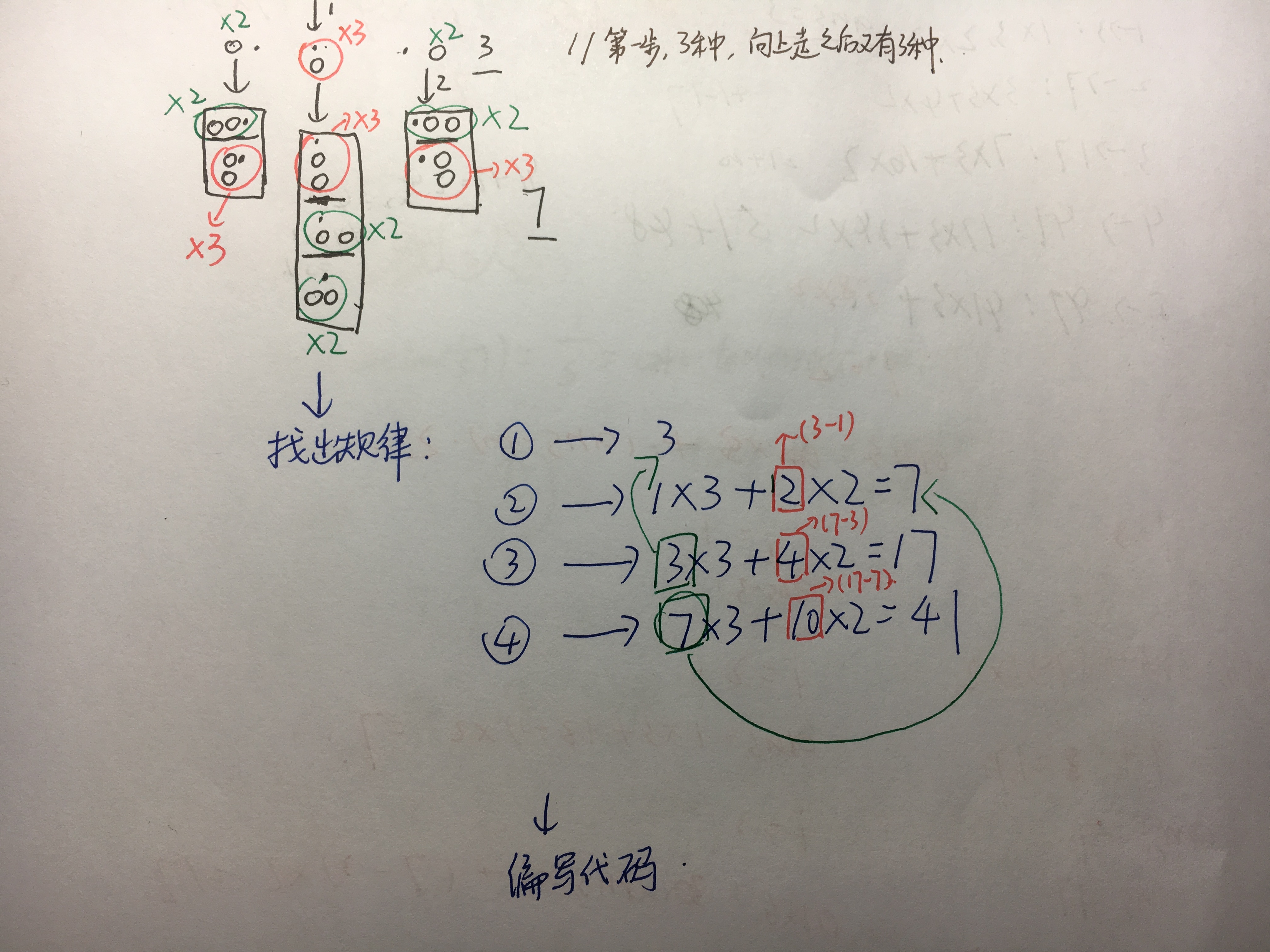
之后根据规律写出代码

#include <iostream>
#include <cstring>
#include <math.h>
#include <algorithm>
#include <cstdio>
#include <stack>
#include <queue>
#include <vector>
#define ll long long
using namespace std;
int t;
int n,ans,ans1,ans2;

int main()
{    cin>>t;
     while(t--)
     {   ans1=3;
         ans2=7;
         ans=7;
         cin>>n;
         if(n==1)
         {
             cout<<"3"<<endl;
             continue;
         }
         if(n==2)
         {
             cout<<"7"<<endl;
             continue;
         }

         for(int i=3;i<=n;i++)
         {       ans=ans1*3+(ans-ans1)*2;
                 ans1=ans2;
                 ans2=ans;
         }
    cout<<ans<<endl;

     }

    return 0;
}

一遍AC