杨辉三角的实现（Java）

杨辉三角的实现

一、什么是杨辉三角

　　杨辉三角是二项式系数在三角形中的一种几何排列。每个数等于它上方两数之和。每行数字左右对称，由1开始逐渐变大。第n行的数字有n项。前n行共[(1+n)n]/2 个数。

　　杨辉三角联系最紧密的是二项式乘方展开式的系数规律，即二项式定理。例如在杨辉三角中，第3行的三个数恰好对应着两数和的平方的展开式的每一项的系数，第4行的四个数恰好依次对应两数和的立方的展开式的每一项的系数，即（a+b）³=a³+3a²b+3ab²+b³，以此类推，杨辉三角是最常见的算法便是用上一行递推计算。

　　杨辉三角是中国古代数学的杰出研究成果之一，把组合数内在的一些代数性质直观地从图形中体现出来，是一种离散型的数与形的结合。

二、代码实现

1.输出10行的杨辉三角

/*
 * 1
 * 11
 * 121
 * 1331
 * ......
 */

public class YangHui
{
    public static void main(String[] args)
    {

        int[][] YangHui=new int[10][];
        for (int i=0;i<YangHui.length;i++)
        {
            YangHui[i]=new int[i+1];//建立二维数组，及行的元素个数

        }
        for (int i=0;i<YangHui.length;i++)
        {
            for (int j=0;j<YangHui[i].length;j++)
            {
/*
        j=0是二位数组第一个元素为0，i=j是在二位数组中最后一个元素
        例：1 YangHui[0][0]
           11 YangHui[1][0] YangHui[1][1]
           121 YangHui[2][0]   ... YangHui[2][2]
 */
                if (j==0||i==j)
                {
                    YangHui[i][j]=1;
                    //先给1行1列；2行1列，2行2列，3行1列，3行3列...赋值为1
                }else
                {
                    YangHui[i][j]=YangHui[i-1][j-1]+YangHui[i-1][j];
                }//再对其他行列进行赋值计算
            }
        }
        for (int i=0;i<YangHui.length;i++)
        {
            for (int m=10;m>i;m--)
            {
                System.out.print("   ");
            }//,将直角三角形的杨辉三角转化成等边三角形的杨辉三角，空格和上层i联系外层i自增，内层m每行自减
            for (int j=0;j<YangHui[i].length;j++)
            {
                System.out.print(YangHui[i][j]+"    ");
                //字符间间隔
            }
            System.out.println();
        }
    }
}

2输入行数再输出

/*
 * 1
 * 11
 * 121
 * 1331
 * ......
 */

import java.util.Scanner;

public class YangHui1
{
    public static void main(String[] args)
    {
        Scanner scanner=new Scanner(System.in);
        System.out.println("请输入需要输出几行的杨辉三角：");
        int x=scanner.nextInt();
        int[][] YangHui=new int[x][];
        for (int i=0;i<YangHui.length;i++)
        {
            YangHui[i]=new int[i+1];//建立二维数组，及行的元素个数

        }
        for (int i=0;i<YangHui.length;i++)
        {
            for (int j=0;j<YangHui[i].length;j++)
            {
/*
        j=0是二位数组第一个元素为0，i=j是在二位数组中最后一个元素
        例：1 YangHui[0][0]
           11 YangHui[1][0] YangHui[1][1]
           121 YangHui[2][0]   ... YangHui[2][2]
 */
                if (j==0||i==j)
                {
                    YangHui[i][j]=1;
                    //先给1行1列；2行1列，2行2列，3行1列，3行3列...赋值为1
                }else
                {
                    YangHui[i][j]=YangHui[i-1][j-1]+YangHui[i-1][j];
                }//再对其他行列进行赋值计算
            }
        }
        for (int i=0;i<YangHui.length;i++)
        {
            for (int m=x;m>i;m--)
            {
                System.out.print("   ");
            }//,将直角三角形的杨辉三角转化成等边三角形的杨辉三角，空格和上层i联系外层i自增，内层m每行自减
            for (int j=0;j<YangHui[i].length;j++)
            {
                System.out.print(YangHui[i][j]+"    ");
                //字符间间隔
            }
            System.out.println();
        }
    }
}

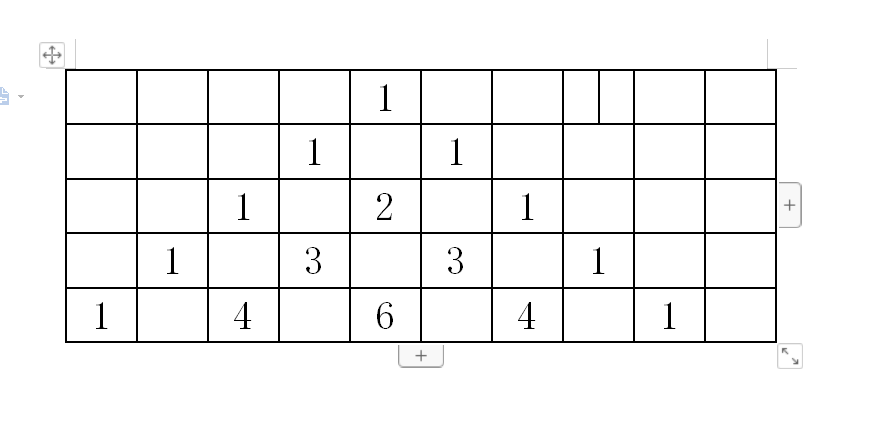
三、大致实现过程

四、总结

　　实现杨辉三角主要使用了二维数组，利用外围数组控制行，内围数组控制列来实现，因为在实现过程中需要计算上一行的数值，所以在计算之前需要给每行第一个元素和最后一个元素赋值为1，这样就可以进行计算了。