题解：2018级算法第六次上机 C6-危机合约

题目描述

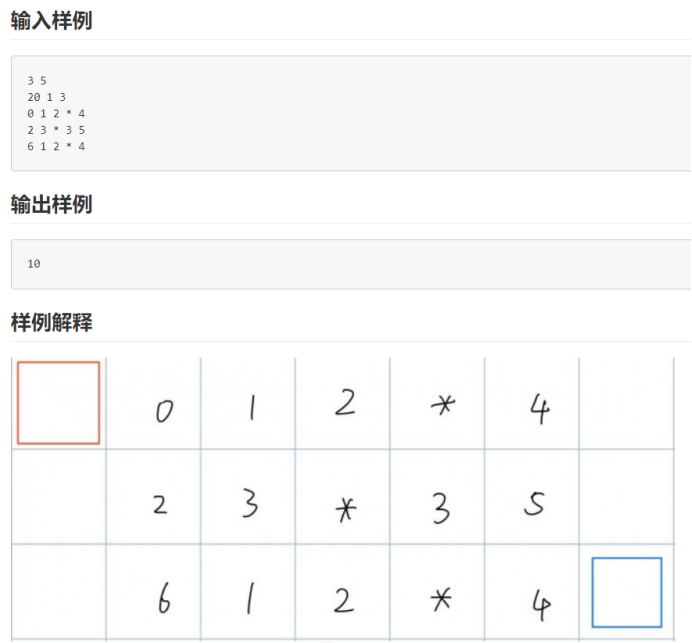
样例：

实现解释：

没想到你也是个刀客塔之二维DP

知识点：

动态规划，多条流水线调度？可以看做一种流水线调度

坑点：

输入内容的调整（*的特殊判定），开头结尾的调整策略

从题意可知，要做的就是从起始点移动到蓝点，并且在过程中会有一个值的记录，这就可以和一些基础题目联系起来：捡金币问题，流水线问题等等。

不过注意在使用板子时需要注意值的调度策略：对无法过去的地点，可将敌人攻击值设为99999，即无限，从而在进行动态规划时也可直接参与计算。借助这一攻击无限化的想法，对第一列和最后一列也需要进行处理：无法从开始点直接进入的第一列的值和无法在最后一列到达结束点，同样是到达无意义（无法上下移动），因此设为无穷。

调整之后便可直接借助dp进行，假设dp数组为dp[i][j]：到达第i行j列时的最小受损值。则很容易可得到状态转移方程：dp[i][j] = min(dp[i][j-1],dp[i-1][j-1],dp[i+1][j-1]) + a[i][j];

基于方程递归进行即可，注意dp的初始化（第一列），这里由于是参考多条流水线进行的编写，因此应该会很熟悉。

完整代码：

#include<iostream>
#include<algorithm>
#include<cmath>
using namespace std;
#define NO 99999
int a[][];
int main()
{
    ios::sync_with_stdio(false);
    int n,m;
    cin >> n >> m;
    int a[n][m];
    int dp[n][m];
    int h,from,to;
    char temp;
    cin >> h >> from >> to;
    for(int i = ;i<n;i++)
    {
        for(int j = ;j<=m;j++)
        {
            cin >> temp;//便于比较是否可通行
            if(temp == '*') a[i][j] = NO;//不可通行则设为一定死的值
            else a[i][j] = temp-'';//否则存储数字
        }
    }
    from -= ;
    to -= ;
    //这里是为了和脚标配合进行的处理
    for(int i = ;i<n;i++)
    {
        //第一列中开局不能到达的，最后一列中不能到结束点的
        //相当于不可达，设为大值
        if(abs(from-i) > ) a[i][] = NO;
        if(abs(to-i) > ) a[i][m] = NO;
    }
    for(int i = ;i<n;i++)
    {
        //象征性的初始化，第一列
        dp[i][] = a[i][];
    }
    int tempf;//存储临时的掉血数
    for(int i = ;i<=m;i++)
    {
        for(int j = ;j<n;j++)
        {
            //向右走
            tempf = dp[j][i-]+a[j][i];
            //判断右上和右下
            for(int k = -;k<=;k+=)
            {
                //越界则跳过
                if(j+k<||j+k>n-) continue;
                if(tempf > dp[j+k][i-]+a[j][i])
                {
                    tempf = dp[j+k][i-]+a[j][i];
                }
            }
            dp[j][i] = tempf;
        }
    }
    //获取最小值设为最大值
    tempf = NO;
    for(int k = -;k<=;k++)
    {
        if(to+k<||to+k>n-) continue;//越界跳过
        if(dp[to+k][m] > NO) continue;//有不可达的点，跳过
        if(dp[to+k][m] < tempf) tempf = dp[to+k][m];//最小值
    }
    //判断最小掉血数和hp的关系
    if(tempf-h > ) cout << "doctor win\n";
    else cout << h-tempf << '\n';
    return ;
}