Jmeter的脚本参数化

一、变量

Jmeter中的变量用法：${变量名称}

变量定义：两种

　　1、用户定义变量 User Defined Variables

　　2、用户参数 User Parameters

1.1用户定义变量

步骤：线程组 ->添加->配置元件->用户定于变量

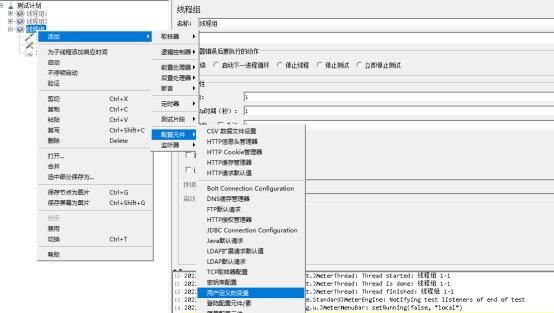
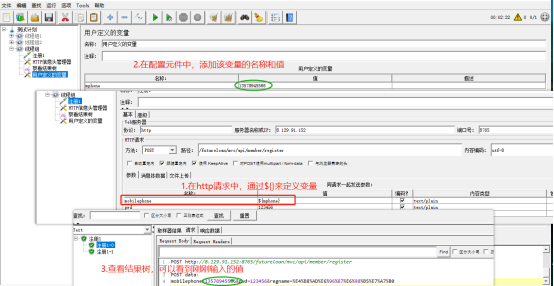
1.2用户参数

步骤：线程组 ->添加->前置处理器->用户参数

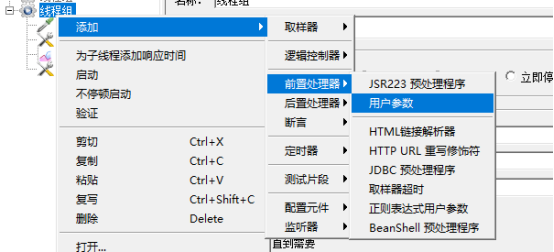
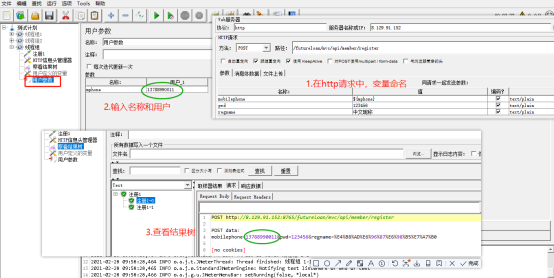
实际上在我们工作中，注册这个接口，是需要不同的手机号码去注册的，如果我每次就算通过变量方式去操作，假如手机号码不变，那跟原来的一个个手动输入值就没什么不同了，也就没必要了；所以我们希望的是它不断的变化

那怎么让它变呢？随机数，如何生成随机数？

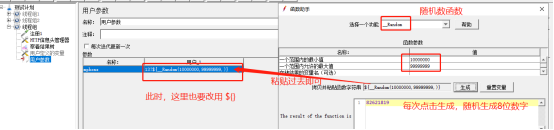
拓展：假如不是号码，公司里面需要大量不同的用户昵称怎么办？相当于随机的用户名怎么办？也就是不同的字母组合合成的字符串；假如我要生成2-8位字符的用户名怎么办？那么，只需要先生成2-8位的随机数即可

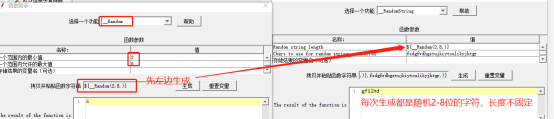
现在，回到正轨，那么用户定义的变量和用户参数有什么异同呢？

共同点：两者均可以用于定义变量

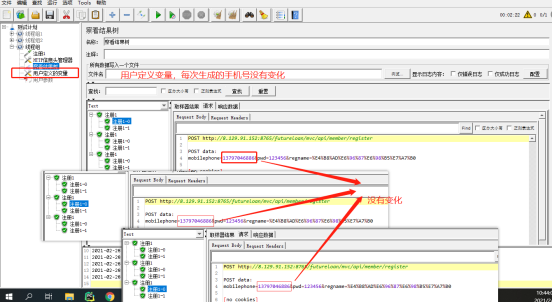
不同点：前提：1个用户，循环3次(跑3次) ，用户定义变量：手机号没有变化，用户参数:手机号会变化

前提：3个用户，循环1次(跑1次)，用户定义变量：手机号没有变化，用户参数:手机号会变化

规律一：用户定义变量，在jmeter启动时，获取一次值，在运行过程中，不再获取值

　　　　用户参数，在jmeter启动时，获取一次值，在运行过程中，还会动态获取值

特点二：用户定义变量，是全局变量；用户参数，是局部变量

二、函数

特别要注意：严格区分大小写和 ${__函数名称（）}

1、__counter：计数器函数
2、__CSVRead：CSV的阉割版
3、__dateTimeConvert：时间转换
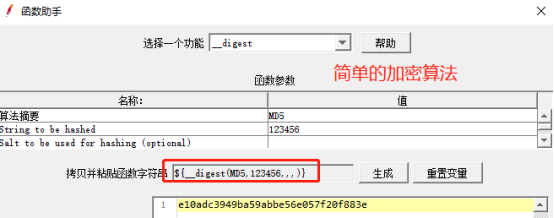
4、__digest：加密算法，支持MD5
5、__machineIP：获取本机器IP
6、__machineName：获取本机器名称
7、__P、__property：获取jmeter属性的函数
8、__setProperty：设置jmeter属性的函数
9、__time：获取当前时间函数
10、__V：拼接函数，将函数拼接在一起

${__counter(,)} 计数器，点击【帮助】可以打开文档

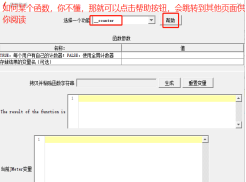
${__digest(MD5,123456,,,)} 加密

${__P(,)}、${__property(,,)} 获取jmeter属性的函数，它们是同一个函数(没有区别)，获取.properties配合文件中属性的值
${__setProperty(,,)} 设置jmeter的属性函数，设置.properties配合文件中属性的值
属性：写在properties文件中的属性，是静态属性，已经写死在文件中；
setProperty函数设置的属性，是动态属性，只对当前启动的jmeter有效，关闭后，自动失效
系统属性:操作系统，字符编码等等；只能获取，读取，不能修改

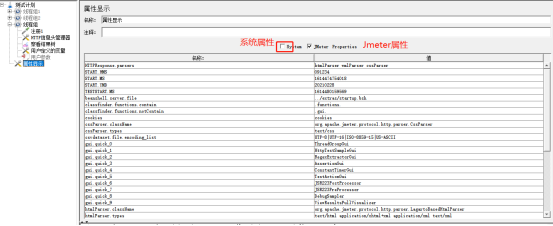
${__time(YMD,)} 获取当前函数

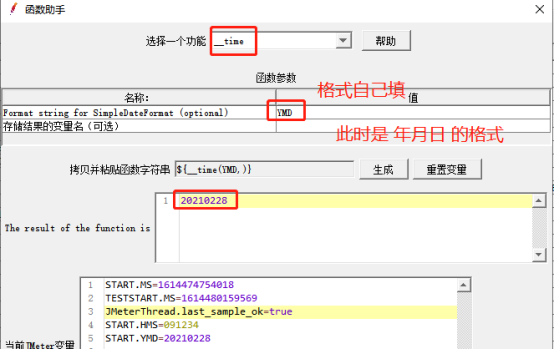
${__V(,)} 拼接函数

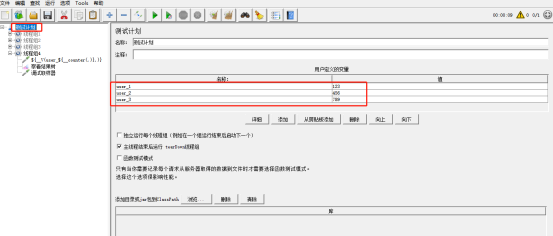
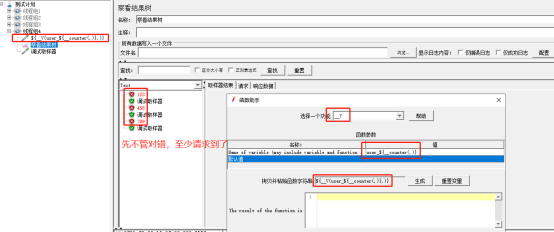
三、CSV配置元件

线程组-->添加-->配置元件-->CSV数据文件设置

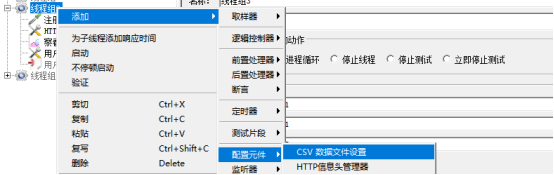
(1)文件名：可用csv和txt文件
　　文件选择，优先选择用txt文件
　　　　原因1：csv消耗资源更多
　　　　原因2：csv文件默认编码不是utf-8，中文可能出现乱码
　　文件路径，优先使用相对路径，为了兼容不同测试员使用
　　　　原因：默认用绝对路径，文件的路径一旦找不到，脚本无法执行
　　　　相对路径写法：相对于当前.jmx文件的位置“./user.txt”
　　　　在上一级文件中：“../user.txt”

(2)分隔符：使用符号分隔参数值
　　csv文件：使用“英文逗号”间隔
　　txt文件：是什么间隔，就用什么符号；
　　　　　　tab键制表符，用“\t”间隔

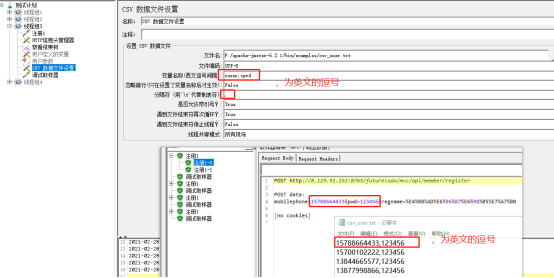
且看一下实际应用截图：

a---------csv文件

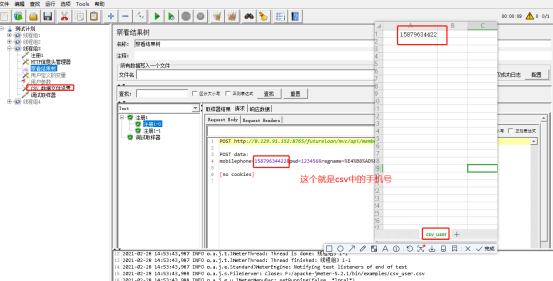
b------------txt文件

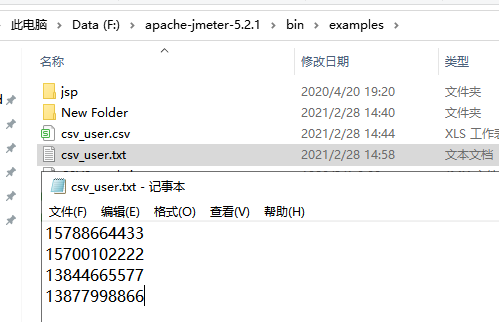
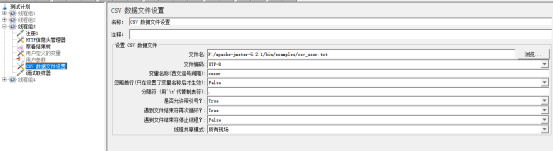
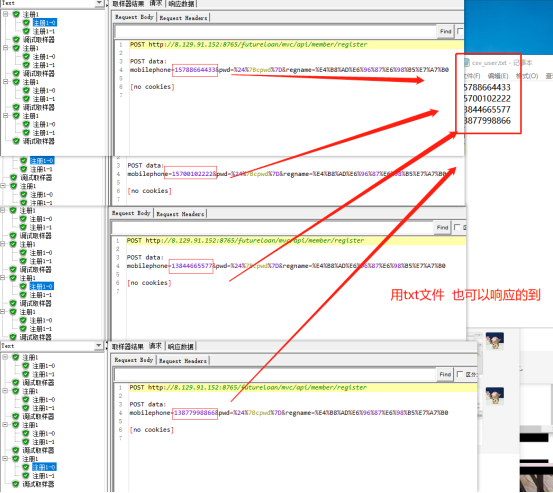
c----------手机号码和密码，两个字段