70.LeetCode爬楼梯

爬楼梯

点击标题可跳转到官网进行查看

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

注意：给定 n 是一个正整数。

示例 1：

输入： 2
输出： 2
解释： 有两种方法可以爬到楼顶。
1.  1 阶 + 1 阶
2.  2 阶

示例 2：

输入： 3
输出： 3
解释： 有三种方法可以爬到楼顶。
1.  1 阶 + 1 阶 + 1 阶
2.  1 阶 + 2 阶
3.  2 阶 + 1 阶

解题思路：

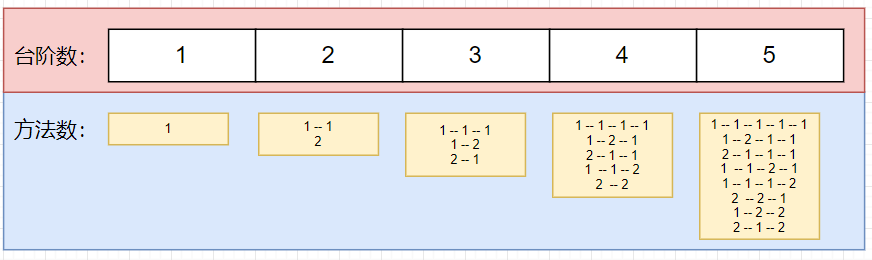
通过举例可以发现，上到n阶的方法数等于“n-1”+“n-2”方法数之和，知道这个规律就可以轻松的写出代码

实现代码：

 1 package easy;
 2 class SolutionCliSta{
 3     public int climbStairs(int n) {
 4         if(n > 0){
 5             int [] dp = new int [n + 2];
 6             dp[1] = 1;
 7             dp[2] = 2;
 8             for (int i =3; i < n + 1; i ++){
 9                 dp[i] = dp [i - 1] + dp[i - 2];
10             }
11             return dp[n];
12         }
13         return 0;
14     }
15 }
16 public class ClimbingStairs {
17     public static void main(String[] args) {
18         SolutionCliSta solution = new SolutionCliSta();
19         System.out.println(solution.climbStairs(0));
20     }
21 }