机器学习之感知器算法原理和Python实现

（1）感知器模型

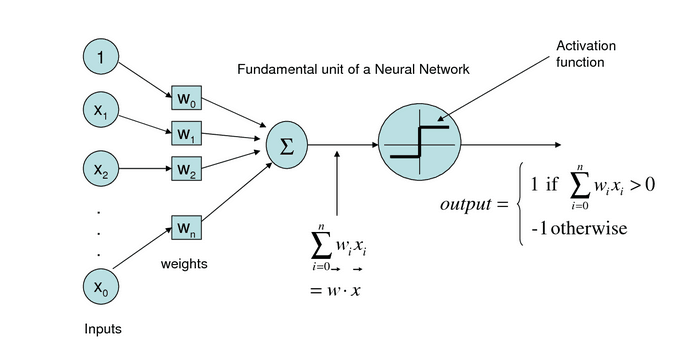
　　感知器模型包含多个输入节点：X0-Xn，权重矩阵W0-Wn（其中X₀和W₀代表的偏置因子，一般X₀=1，图中X₀处应该是X_n）一个输出节点O，激活函数是sign函数。

　　（2）感知器学习规则

　　

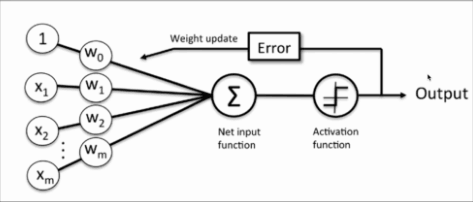
　　输入训练样本X和初始权重向量W，将其进行向量的点乘，然后将点乘求和的结果作用于激活函数sign（），得到预测输出O，根据预测输出值和目标值之间的差距error，来调整初始化权重向量W。如此反复，直到W调整到合适的结果为止。

（3）算法的原始形式

（4）Python代码实现

 import numpy as np

 class Perceptron(object):

     """Perceptron classifier(感知器分类器)

     Parameters(参数)
     ---------------
     eta:float 学习率
         Learning rate(between 0.0 and 1.0)
     n_iter:int 权重向量的训练次数
         Passes over training dataset 

     Attributes(属性)
     --------------
     w_:1d_array 一维权重向量
         Weights after fitting
     errors_:list 记录神经元判断错误的次数
         Number of misclassifications in every epoch
     """

     #初始化对象
     def __init__(self,eta=0.01,n_iter=10):
         self.eta=eta
         self.n_iter=n_iter

     #训练模型
     def fit(self,X,y):
         """
         fit training data.(拟合训练数据)

         Parameters(参数)
         ----------------
        :param x: list[np.array] 一维数组数据集
         :param y: 被训练的数据集的实际结果
         :return:
           权值，初始化为一个零向量R的(m+1)次方，m代表数据集中纬度（特征）的数量
           x.shape[1] = (100,2) 一百行2列：表示数据集中的列数即特征数

           np.zeros(count) 将指定数量count初始化成元素均为0的数组 self.w_ = [ 0.  0.  0.]
         """

         #初始化权重和错误列表
         self.w_=np.zeros(1+X.shape[1])
         self.errors_=[]

         for _ in range(self.n_iter):
             errors=0
             for xi,target in zip(X,y):
                 #计算预测与实际值之间的误差在乘以学习率
                 update=self.eta*(target-self.predict(xi))
                 self.w_[1:]+=update*xi
                 self.w_[0]+=update*1
                 errors += int(update!=0)
                 self.errors_.append(errors)
             return self

     #定义感知器的传播过程
     def net_input(self,X):
         """
         计算净输入
         :param x: list[np.array] 一维数组数据集
         :return: 计算向量的点积
             向量点积的概念：
                 {1，2，3} * {4，5，6} = 1*4+2*5+3*6 = 32

         description:
             sum(i*j for i, j in zip(x, self.w_[1:])) python计算点积
         """
         print(X,end="  ")
         print(self.w_[:],end="  ")
         X_dot=np.dot(X,self.w_[1:])+self.w_[0]
         print("的点积是：%d" % X_dot,end="  ")
         return X_dot

     #定义预测函数
     def predict(self,X):
         target_pred=np.where(self.net_input(X)>=0.0,1,-1)
         print("预测值：%d" % target_pred,end="  ")
         return target_pred