二叉树及其遍历方法---python实现

github：代码实现

本文算法均使用python3实现

---

1. 二叉树

1.1 二叉树的定义

  二叉树是一种特殊的树，它具有以下特点：

  （1）树中每个节点最多只能有两棵树，即每个节点的度最多为2。

  （2）二叉树的子树有左右之分，即左子树与右子树，次序不能颠倒。

  （3）二叉树即使只有一个子树时，也要区分是左子树还是右子树。

1.2 满二叉树

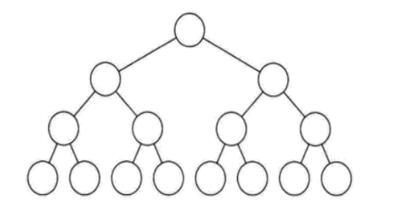
  满二叉树作为一种特殊的二叉树，它是指：所有的分支节点都存在左子树与右子树，并且所有的叶子节点都在同一层上。其特点有：

  （1）叶子节点只能出现在最下面一层

  （2）非叶子节点度一定是2

  （3）在同样深度的二叉树中，满二叉树的节点个数最多，节点个数为： $ 2^h -1 $ ，其中 $ h $ 为树的深度。

1.3 完全二叉树

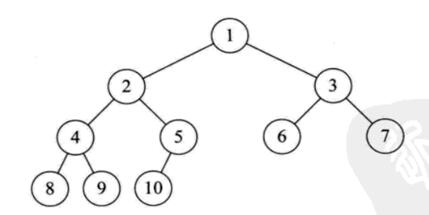
  若设二叉树的深度为 $ h $ ，除第 $ h $ 层外，其它各层 $ (1～h-1) $ 的结点数都达到最大个数，第 $ h $ 层所有的结点都连续集中在最左边，这就是完全二叉树。其具有以下特点：

  （1）叶子节点可以出现在最后一层或倒数第二层。

  （2）最后一层的叶子节点一定集中在左部连续位置。

  （3）完全二叉树严格按层序编号。（可利用数组或列表进行实现，满二叉树同）

  （4）若一个节点为叶子节点，那么编号比其大的节点均为叶子节点。

---

2. 二叉树的相关性质

2.1 二叉树性质

  （1）在非空二叉树的 $ i $ 层上，至多有 $ 2^{i-1} $ 个节点 $ (i \geq 1) $ 。

  （2）在深度为 $ h $ 的二叉树上最多有 $ 2^h -1 $ 个节点 $（k \geq 1) $ 。

  （3）对于任何一棵非空的二叉树,如果叶节点个数为 $ n_0 $ ，度数为 $ 2 $ 的节点个数为 $ n_2 $ ，则有: $ n_0 = n_2 + 1 $ 。

2.1 完全二叉树性质

  （1）具有 $ n $ 个的结点的完全二叉树的深度为 $ \log_2{n+1} $ 。.

  （2）如果有一颗有 $ n $ 个节点的完全二叉树的节点按层次序编号，对任一层的节点 $ i ，（1 \geq i \geq n）$ 有：

    （2.1）如果 $ i=1 $ ，则节点是二叉树的根，无双亲，如果 $ i>1 $ ，则其双亲节点为 $ \lfloor i/2 \rfloor $ 。

    （2.2）如果 $ 2i>n $ 那么节点i没有左孩子，否则其左孩子为 $ 2i $ 。

    （2.3）如果 $ 2i+1>n $ 那么节点没有右孩子，否则右孩子为 $ 2i+1 $ 。

---

3. 二叉树的遍历

  以下遍历以该二叉树为例：

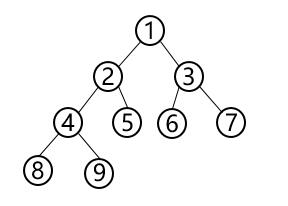
3.1 前序遍历

  思想：先访问根节点，再先序遍历左子树，然后再先序遍历右子树。总的来说是根—左—右

  上图先序遍历结果为为：$ 1,2,4,8,9,5,3,6,7 $

  代码如下：

	def PreOrder(self, root):
		'''打印二叉树(先序)'''
		if root == None:
			return
		print(root.val, end=' ')
		self.PreOrder(root.left)
		self.PreOrder(root.right)

3.2 中序遍历

  思想：先中序访问左子树，然后访问根，最后中序访问右子树。总的来说是左—根—右

  上图中序遍历结果为为：$ 8,4,9,2,5,1,6,3,7 $

  代码如下：

	def InOrder(self, root):
		'''中序打印'''
		if root == None:
			return
		self.InOrder(root.left)
		print(root.val, end=' ')
		self.InOrder(root.right)

3.3 后序遍历

  思想：先后序访问左子树，然后后序访问右子树，最后访问根。总的来说是左—右—根

  上图后序遍历结果为为：$ 8,9,4,5,2,6,7,3,1 $

  代码如下：

	def BacOrder(self, root):
		'''后序打印'''
		if root == None:
			return
		self.BacOrder(root.left)
		self.BacOrder(root.right)
		print(root.val, end=' ')

3.4 层次遍历（宽度优先遍历）

  思想：利用队列，依次将根，左子树，右子树存入队列，按照队列的先进先出规则来实现层次遍历。

  上图后序遍历结果为为：$ 1,2,3,4,5,6,7,8,9 $

  代码如下：

	def BFS(self, root):
		'''广度优先'''
		if root == None:
			return
		# queue队列，保存节点
		queue = []
		# res保存节点值，作为结果
		#vals = []
		queue.append(root)

		while queue:
			# 拿出队首节点
			currentNode = queue.pop(0)
			#vals.append(currentNode.val)
			print(currentNode.val, end=' ')
			if currentNode.left:
				queue.append(currentNode.left)
			if currentNode.right:
				queue.append(currentNode.right)
		#return vals

3.5 深度优先遍历

  思想：利用栈，先将根入栈，再将根出栈，并将根的右子树，左子树存入栈，按照栈的先进后出规则来实现深度优先遍历。

  上图后序遍历结果为为：$ 1,2,4,8,9,5,3,6,7 $

  代码如下：

	def DFS(self, root):
		'''深度优先'''
		if root == None:
			return
		# 栈用来保存未访问节点
		stack = []
		# vals保存节点值，作为结果
		#vals = []
		stack.append(root)

		while stack:
			# 拿出栈顶节点
			currentNode = stack.pop()
			#vals.append(currentNode.val)
			print(currentNode.val, end=' ')
			if currentNode.right:
				stack.append(currentNode.right)
			if currentNode.left:
				stack.append(currentNode.left)
		#return vals

3.6 代码运行结果

---

引用及参考：

[1]《数据结构》李春葆著

[2] http://www.cnblogs.com/polly333/p/4740355.html

写在最后：本文参考以上资料进行整合与总结，属于原创，文章中可能出现理解不当的地方，若有所见解或异议可在下方评论，谢谢！

若需转载请注明：https://www.cnblogs.com/lliuye/p/9143676.html