【RL系列】Multi-Armed Bandit笔记补充（一）

在此之前，请先阅读上一篇文章：【RL系列】Multi-Armed Bandit笔记

本篇的主题就如标题所示，只是上一篇文章的补充，主要关注两道来自于Reinforcement Learning: An Introduction 的课后习题。

第一题为Exercise 2.5 (programming)，主要讨论了Recency-Weighted Average算法相较于Sample Average算法的优点所在。练习内容大致为比较这两种算法在收益分布为非平稳分布的情况下的表现情况，主要的评价指标依照Figure 2.2，也就是Average Reward和Optimal Action Rate两个。

先前我们在上一篇文章中讨论的所有情况都是假设收益分布为一个固定的不变的正态分布，比如N(1, 1)，这里可以称其为平稳分布(Stationary Distribution)。那么如何制造一个非平稳分布呢？在练习中，已经给出了提示：在每一步的实验中，在实际收益均值上加一个服从标准差差为0.01，均值为0的正态分布的随机数即可，举个例子，N(1 + N(0, 0.01), 1)。那么在原先的Matlab程序中需要做出如下的修改：

% 10-Armed Bandit
K = 10;
AverReward = randn([1 K]);
% Reward for each Action per experiment
% Reward(Action) = normrnd(AverReward(Action) + normrnd(0, 0.01), 1);

　　

学习过程的参数设定为epsilon = 0.1，最终step数设为10000：

第二题为Exercise 2.6，这个问题是关于初值优化的，主要讨论了初值优化后的OAR图像为何会在实验次数较少时出现突然的尖峰，这个问题也被称作Mysterious Spike：

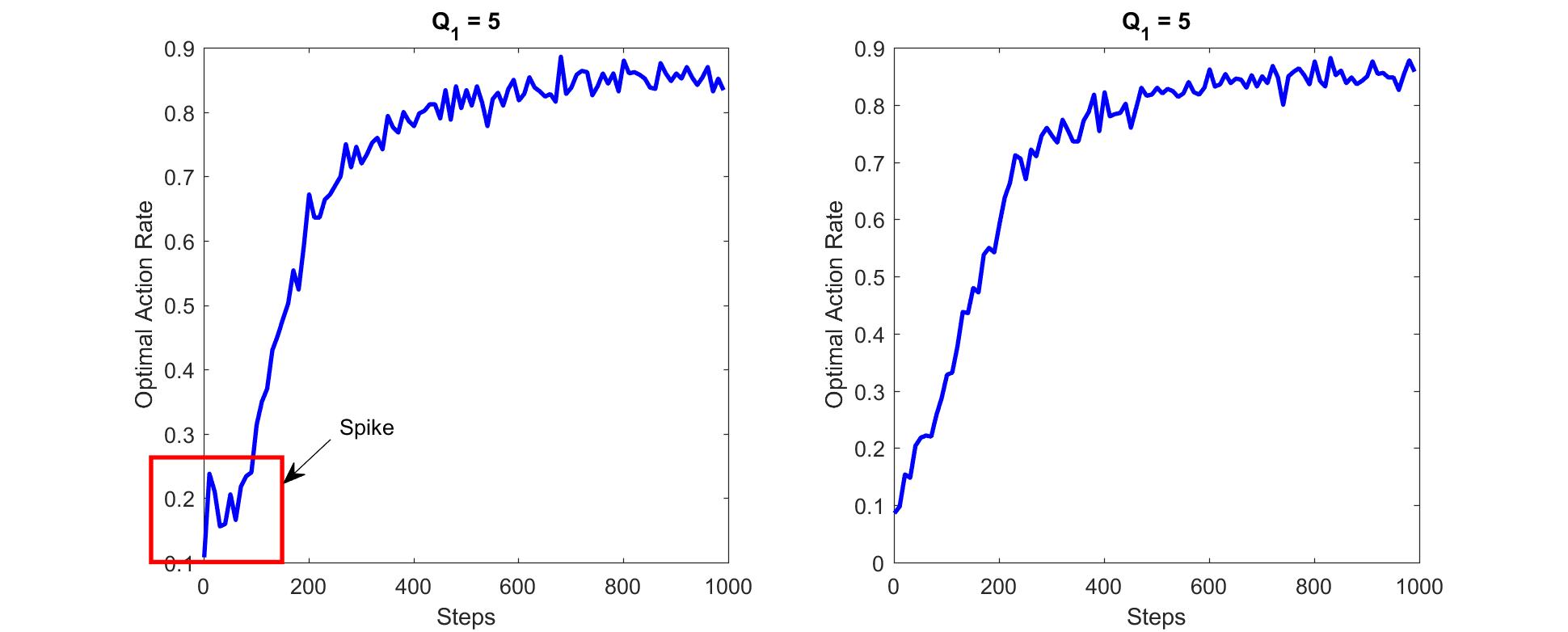
假设我们将初值Q1设为5，最终step数设为1000，epsilon = 0。可以发现左图的greedy策略是直接求解Q值中的最大值所对应的动作，如下将其转化为Matlab

[MAX i] = max(Q);
if(rand(1) < 1 - epsilon)
    CurrentA = i;
else
    CurrentA = unidrnd(RandK);
end

而右图也同样是将初值设为5，但并未出现Spike现象，给出右图的greedy选择策略：

[MAX i] = max(Q);
if(MAX ~= 5 & rand(1) < 1 - epsilon)
    CurrentA = i;
else
    CurrentA = unidrnd(RandK);
end

　　

出现Spike现象的原因其实很简单，如果一向量或序列存在两个或两个以上相同的最大值时，计算机在计算最值所在位置的返回值一定是第一个最大值的位置。举个例子（Matlab）

x = [1 2 5 5 5 1]
[MAX n] = max(x);

>> MAX = 5
>> n = 3

这个例子中一定不会出现n = 4或n= 5，这就造成了一个问题，我们总是会在有限的步数内不断的去逼近那个真实的收益均值最大值所在的位置。那么在计算Optimal Action Rate时，我们可以举个例子，假设现在是10-Armed Bandit问题，而step数只有不到十次，我们就只看5次的情况吧，假设我们的真实收益最大均值就在向量的第五个位置。

N = 7
K = 10
Reward = [1 2 3 4 5 4.5 3.5 2.5 1.5 0.5];
[MAX i] = max(Reward);
>> MAX = 5
>> i = 5

Q = zeros(1, K) + 5;

% First step
[MAXQ i] = max(Q);
>> i = 1
>> Q = [4.6 5 5 5 5 5 5 5 5 5]
>> OAR = 0

% Second step
[MAXQ i] = max(Q);
>> i = 2
>> Q = [4.6 4.7 5 5 5 5 5 5 5 5]
>> OAR = 0

.....

% 5th step
[MAX i] = max(Q);
>> i = 5
>> Q = [4.6 4.7 4.8 4.9 5 5 5 5 5 5]
>> OAR = 0.2
%Notice that here's a Spike!

所以依据上面的推断，我们可以推测出，Spike的发生大概率出现在K次实验内（K为K-Armed中的K），而且Spike的最高值取决于真实的收益均值所在的位置与K值之比，假设其所在位置为第M位，则Spike的值可以估计为M/K。当实验次数大于K时，OAR则会从1/K开始逐步增加。