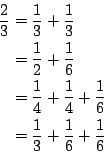[POJ1980]Unit Fraction Partition(搜索)
Unit Fraction Partition
Time Limit: 1000MS Memory Limit: 30000K Total Submissions: 4571 Accepted: 1809 Description
A fraction whose numerator is 1 and whose denominator is a positive integer is called a unit fraction. A representation of a positive rational number p/q as the sum of finitely many unit fractions is called a partition of p/q into unit fractions. For example, 1/2 + 1/6 is a partition of 2/3 into unit fractions. The difference in the order of addition is disregarded. For example, we do not distinguish 1/6 + 1/2 from 1/2 + 1/6.For given four positive integers p, q, a, and n, count the number of
partitions of p/q into unit fractions satisfying the following two
conditions.The partition is the sum of at most n many unit fractions.
The product of the denominators of the unit fractions in the partition is less than or equal to a.
For example, if (p,q,a,n) = (2,3,120,3), you should report 4 since
enumerates all of the valid partitions.Input
The input is a sequence of at most 200 data sets followed by a terminator.A data set is a line containing four positive integers p, q, a, and n
satisfying p,q <= 800, a <= 12000 and n <= 7. The integers are
separated by a space.The terminator is composed of just one line which contains four
zeros separated by a space. It is not a part of the input data but a
mark for the end of the input.Output
The
output should be composed of lines each of which contains a single
integer. No other characters should appear in the output.The output integer corresponding to a data set p, q, a, n should be
the number of all partitions of p/q into at most n many unit fractions
such that the product of the denominators of the unit fractions is less
than or equal to a.Sample Input
2 3 120 3
2 3 300 3
2 3 299 3
2 3 12 3
2 3 12000 7
54 795 12000 7
2 3 300 1
2 1 200 5
2 4 54 2
0 0 0 0Sample Output
4
7
6
2
42
1
0
9
3Source
沦落到要做普及组题目的地步了吗。。发现自己连搜索都不会写了。
几个可行性剪枝就可以了:乘积不超限,个数不超限,分数和不超过目标。
起先一直TLE,把循环中的除法提到外面就卡过了。
这种题目竟然也要做1h。。
#include<cstdio>
#include<algorithm>
#define rep(i,l,r) for (int i=l; i<=r; i++)
using namespace std; int p,q,a,n,ans; void dfs(int mn,int num,int deno,int mul,int dq){
if (mul>a) return;
if (num*q==deno*p) ans++;
if (num*q>deno*p || dq==n) return;
int t=a/mul;
rep(i,mn,t) dfs(i,num*i+deno,deno*i,mul*i,dq+);
} int main(){
freopen("poj1980.in","r",stdin);
freopen("poj1980.out","w",stdout);
while (~scanf("%d%d%d%d",&p,&q,&a,&n)){
if (q==) return ;
ans=; dfs(,,,,); printf("%d\n",ans);
}
return ;
}
[POJ1980]Unit Fraction Partition(搜索)的更多相关文章
- 【题解】Unit Fraction Partition-C++
Description给出数字P,Q,A,N,代表将分数P/Q分解成至多N个分数之和,这些分数的分子全为1,且分母的乘积不超过A.例如当输入数据为2 3 120 3时,我们可以得到以下几种分法: In ...
- AHOI2018训练日程(3.10~4.12)
(总计:共90题) 3.10~3.16:17题 3.17~3.23:6题 3.24~3.30:17题 3.31~4.6:21题 4.7~4.12:29题 ZJOI&&FJOI(6题) ...
- Hadoop官方文档翻译——MapReduce Tutorial
MapReduce Tutorial(个人指导) Purpose(目的) Prerequisites(必备条件) Overview(综述) Inputs and Outputs(输入输出) MapRe ...
- 泛函编程(34)-泛函变量:处理状态转变-ST Monad
泛函编程的核心模式就是函数组合(compositionality).实现函数组合的必要条件之一就是参与组合的各方程序都必须是纯代码的(pure code).所谓纯代码就是程序中的所有表达式都必须是Re ...
- Delphi XE5教程8:使用Delphi命名空间
// Project file declarations... //项目文件声明… program MyCompany.ProjectX.ProgramY; // Unit source file d ...
- project euler 26:Reciprocal cycles
A unit fraction contains 1 in the numerator. The decimal representation of the unit fractions with d ...
- Spark Sort-Based Shuffle具体实现内幕和源码详解
为什么讲解Sorted-Based shuffle?2方面的原因:一,可能有些朋友看到Sorted-Based Shuffle的时候,会有一个误解,认为Spark基于Sorted-Based Shuf ...
- (转)Oracle分区表和索引的创建与管理
今天用到了Oracle表的分区,就顺便写几个例子把这个表的分区说一说: 一.创建分区表 1.范围分区 根据数据表字段值的范围进行分区 举个例子,根据学生的不同分数对分数表进行分区,创建一个分区表如下: ...
- linux 文件的查找和压缩
1.使用 locate 命令 需要安装:yum install mlocate -y 创建或更新 slocate/locate 命令所必需的数据库文件:updatedb 作用:搜索不经常改变的文件如配 ...
随机推荐
- bzoj 4034: [HAOI2015]树上操作——树链剖分
Description 有一棵点数为 N 的树,以点 1 为根,且树点有边权.然后有 M 个 操作,分为三种: 操作 1 :把某个节点 x 的点权增加 a . 操作 2 :把某个节点 x 为根的子树中 ...
- 【51NOD-0】1130 N的阶乘的长度 V2(斯特林近似)
[算法]数学 [题解]斯特林公式: #include<cstdio> #include<algorithm> #include<cmath> using names ...
- .NET FrameWork 中的 CTS
CTS:Common Type System 通用类型系统. 1.不仅可以把C#编译成.Net IL,还支持Basic.Python.Ruby等语言,甚至还支持Java.不同语言中的数据类型定义是不一 ...
- 分布式实时日志分析解决方案ELK部署架构
一.概述 ELK 已经成为目前最流行的集中式日志解决方案,它主要是由Beats.Logstash.Elasticsearch.Kibana等组件组成,来共同完成实时日志的收集,存储,展示等一站式的解决 ...
- 网络协议之HTTP协议
HTTP协议详解(真的很经典) 转自:http://blog.csdn.net/gueter/archive/2007/03/08/1524447.aspx Author :Jeffrey 引言 HT ...
- POJ1014(多重背包)
Dividing Time Limit: 1000MS Memory Limit: 10000K Total Submissions: 65044 Accepted: 16884 Descri ...
- C 封装一个通用链表 和 一个简单字符串开发库
引言 这里需要分享的是一个 简单字符串库和 链表的基库,代码也许用到特定技巧.有时候回想一下, 如果我读书的时候有人告诉我这些关于C开发的积淀, 那么会走的多直啊.刚参加工作的时候做桌面开发, 服务是 ...
- webapi-1 给现有MVC 项目添加 WebAPI
1. 增加一个WebApi Controller, VS 会自动添加相关的引用,主要有System.Web.Http,System.Web.Http.WebHost,System.Net.Http 2 ...
- 构造函数、原型对象prototype、实例、隐式原型__proto__的理解
(欢迎一起探讨,如果有什么地方写的不准确或是不正确也欢迎大家指出来~) PS: 内容中的__proto__可能会被markdown语法导致显示为proto. 建议将构造函数中的方法都定义到构造函数的原 ...
- Mybatis学习 PageHelper分页插件
1.Maven依赖,注意使用PageHelper时的版本必须与Mybatis版本对应 1 <!-- 添加Mybatis依赖 --> 2 <dependency> 3 <g ...