【manacher】HDU3068-最长回文

【题目大意】

给出一个只由小写英文字符a,b,c...y,z组成的字符串S,求S中最长回文串的长度。

【manacher知识点】

①mx - i > P[j] 的时候，以S[j]为中心的回文子串包含在以S[id]为中心的回文子串中，由于 i 和 j 对称，以S[i]为中心的回文子串必然包含在以S[id]为中心的回文子串中，所以必有 P[i] = P[j]。

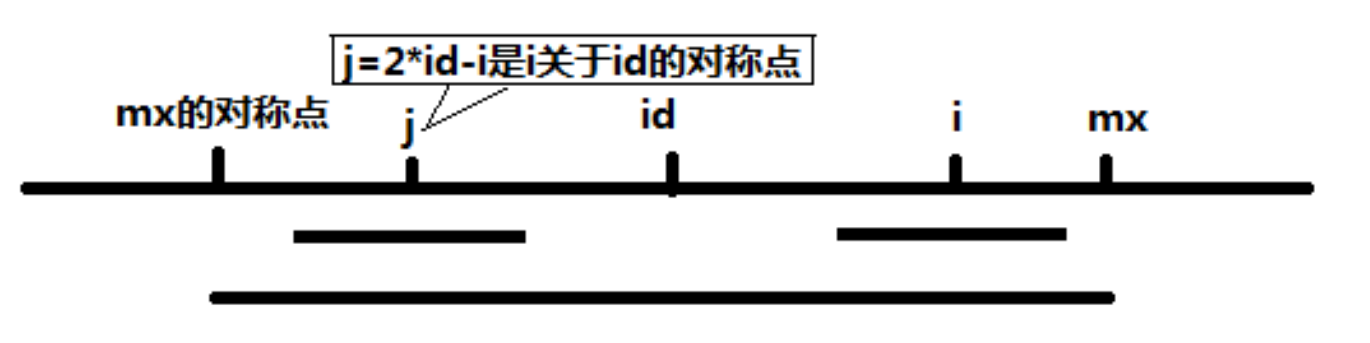
②当 P[j] > mx - i 的时候，以S[j]为中心的回文子串不完全包含于以S[id]为中心的回文子串中，但是基于对称性可知，下图中两个绿框所包围的部分是相同的，也就是说以 S[i]为中心的回文子串，其向右至少会扩张到mx的位置，也就是说 P[i] >= mx - i。至于mx之后的部分是否对称，就只能一个一个匹配了。

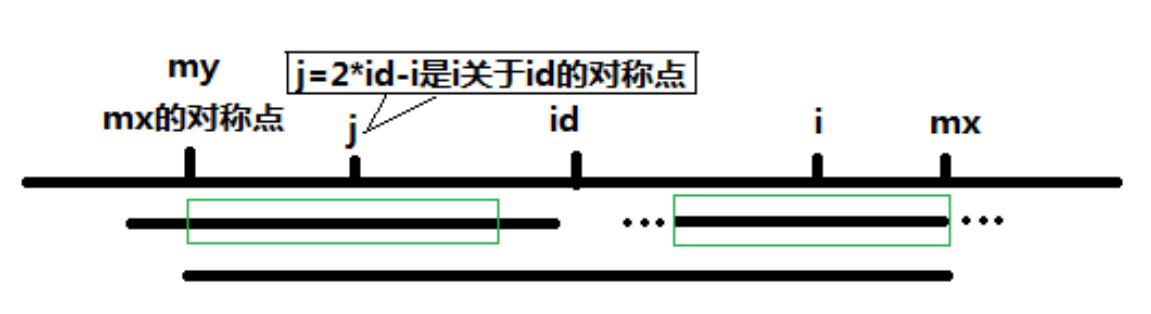
③对于 mx <= i 的情况，无法对 P[i]做更多的假设，只能P[i] = 1，然后再去匹配了

 #include<iostream>
 #include<algorithm>
 #include<cstdio>
 #include<cstdlib>
 #include<cstring>
 using namespace std;
 const int MAXN=+;
 char str[MAXN],s[MAXN*];
 int p[MAXN*]; 

 void init()
 {
     s[]='$';s[]='#';
     int j=;
     for (int i=;str[i];i++)
     {
         s[++j]=str[i];
         s[++j]='#';
     }
     //cout<<s<<endl;
 }

 void solve()
 {
     int mx=,mxid=;
     memset(p,,sizeof(p));
     for (int i=;s[i];i++)
     {
         if (mx>i) p[i]=(p[*mxid-i]<(mx-i)?p[*mxid-i]:(mx-i));
             else p[i]=;
         while(s[i-p[i]]==s[i+p[i]]) p[i]++;
         if (i+p[i]>mx)
         {
             mx=i+p[i];
             mxid=i;
         }
     }
 }

 int getans()
 {
     int len=strlen(str)*+;
     int ans=-;
     for (int i=;i<len;i++) ans=max(ans,p[i]);
     ans--;
     return ans;
 }

 int main()
 {
     while (scanf("%s",str)!=EOF)
     {
         init();
         solve();
         cout<<getans()<<endl;
     }
     return ;
 }