Codeforces Round #483 (Div. 2) [Thanks, Botan Investments and Victor Shaburov!]

题目链接：http://codeforces.com/contest/984

A. Game

time limit per test：2 seconds

memory limit per test：512 megabytes

input：standard input

output：standard output

Two players play a game.

Initially there are nn integers a1,a2,…,ana1,a2,…,an written on the board. Each turn a player selects one number and erases it from the board. This continues until there is only one number left on the board, i. e. n−1n−1 turns are made. The first player makes the first move, then players alternate turns.

The first player wants to minimize the last number that would be left on the board, while the second player wants to maximize it.

You want to know what number will be left on the board after n−1n−1 turns if both players make optimal moves.

Input

The first line contains one integer nn (1≤n≤10001≤n≤1000) — the number of numbers on the board.

The second line contains nn integers a1,a2,…,ana1,a2,…,an (1≤ai≤1061≤ai≤106).

Output

Print one number that will be left on the board.

Examples

Input

Copy

3
2 1 3

Output

Copy

2

Input

Copy

3
2 2 2

Output

Copy

2

Note

In the first sample, the first player erases 33 and the second erases 11. 22 is left on the board.

In the second sample, 22 is left on the board regardless of the actions of the players.

题意：给你n个数，求出排在中间的那个数，签到题。

代码实现如下：

 #include <bits/stdc++.h>
 using namespace std;

 int n;
 int a[];

 int main() {
     cin >>n;
     for(int i = ; i < n; i++) {
         cin >>a[i];
     }
     sort(a, a + n);
     if(n %  == ) {
         cout <<a[n/] <<endl;
     } else {
         cout <<a[(n-) / ] <<endl;
     }
     return ;
 }

B. Minesweeper

time limit per test：2 seconds

memory limit per test：512 megabytes

input：standard input

output：standard output

One day Alex decided to remember childhood when computers were not too powerful and lots of people played only default games. Alex enjoyed playing Minesweeper that time. He imagined that he saved world from bombs planted by terrorists, but he rarely won.

Alex has grown up since then, so he easily wins the most difficult levels. This quickly bored him, and he thought: what if the computer gave him invalid fields in the childhood and Alex could not win because of it?

He needs your help to check it.

A Minesweeper field is a rectangle n×mn×m, where each cell is either empty, or contains a digit from 11 to 88, or a bomb. The field is valid if for each cell:

• if there is a digit kk in the cell, then exactly kk neighboring cells have bombs.
• if the cell is empty, then all neighboring cells have no bombs.

Two cells are neighbors if they have a common side or a corner (i. e. a cell has at most 88 neighboring cells).

Input

The first line contains two integers nn and mm (1≤n,m≤1001≤n,m≤100) — the sizes of the field.

The next nn lines contain the description of the field. Each line contains mm characters, each of them is "." (if this cell is empty), "*" (if there is bomb in this cell), or a digit from 11 to 88, inclusive.

Output

Print "YES", if the field is valid and "NO" otherwise.

You can choose the case (lower or upper) for each letter arbitrarily.

Examples

Input

Copy

3 3
111
1*1
111

Output

Copy

YES

Input

Copy

2 4
*.*.
1211

Output

Copy

NO

Note

In the second example the answer is "NO" because, if the positions of the bombs are preserved, the first line of the field should be *2*1.

You can read more about Minesweeper in Wikipedia's article.

题意：扫雷游戏，让你判断他给你的图是否合法（.表示周围八格里面没有雷，*表示雷，数字表示周围有几颗雷）。

思路：用一个dfs跑一个标准图出来，然后进行对照即可。

代码实现如下：

 #include <bits/stdc++.h>
 using namespace std;

 int n, m;
 char mp[][], check[][];
 int vis[][];

 void dfs(int x, int y) {
     vis[x][y] = ;
     int cnt = ;
     for(int i = -; i < ; i++) {
         for(int j = -; j < ; j++) {
             if(i ==  && j == ) continue;
             int nx = x + i, ny = y + j;
             if(nx >=  && nx < n && ny >=  && ny < m) {
                 if(check[nx][ny] == '*') cnt++;
                 if(vis[nx][ny] == ) {
                     dfs(nx, ny);
                 }
             }
         }
     }
     if(cnt && check[x][y] == '.') {
         check[x][y] = cnt + '';
     }
 }

 int main() {
     cin >>n >>m;
     for(int i = ; i < n; i++) {
         cin >>mp[i];
     }
     for(int i = ; i < n; i++) {
         for(int j = ; j < m; j++) {
             if(mp[i][j] == '*') {
                 check[i][j] = '*';
             } else {
                 check[i][j] = '.';
             }
         }
     }
     dfs(, );
     int flag = ;
     for(int i = ; i < n; i++) {
         for(int j = ; j < m; j++) {
             if(mp[i][j] != check[i][j]) {
                 flag = ;
                 break;
             }
         }
     }
     if(flag) cout <<"YES" <<endl;
     else cout <<"NO" <<endl;
     return ;
 }

C. Finite or not?

time limit per test：2 seconds

memory limit per test：512 megabytes

input：standard input

output：standard output

You are given several queries. Each query consists of three integers pp, qq and bb. You need to answer whether the result of p/qp/q in notation with base bb is a finite fraction.

A fraction in notation with base bb is finite if it contains finite number of numerals after the decimal point. It is also possible that a fraction has zero numerals after the decimal point.

Input

The first line contains a single integer nn (1≤n≤1051≤n≤105) — the number of queries.

Next nn lines contain queries, one per line. Each line contains three integers pp, qq, and bb (0≤p≤10180≤p≤1018, 1≤q≤10181≤q≤1018, 2≤b≤10182≤b≤1018). All numbers are given in notation with base 1010.

Output

For each question, in a separate line, print Finite if the fraction is finite and Infinite otherwise.

Examples

Input

Copy

2
6 12 10
4 3 10

Output

Copy

Finite
Infinite

Input

Copy

4
1 1 2
9 36 2
4 12 3
3 5 4

Output

Copy

Finite
Finite
Finite
Infinite

Note

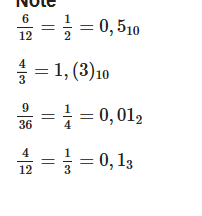
题意：给你一个p,q,b，问p/q在b进制下是否为有限小数。

思路：数论题，方法为判断b的x次方是否能整除q。一开始我用的是唯一分解定理，但是一直T，从T10->WA7->T11，然后本以为接近正理了，然后就没有然后了，其实这题可以用gcd来将q进行消去因子，最后判断q是否等于1。注意小trick，不然还是会T。

代码实现如下：

 #include <bits/stdc++.h>
 using namespace std;

 typedef long long ll;
 int n;
 ll p, q, b;

 ll gcd(ll a, ll b) {
     return (b == ) ? a : gcd(b, a % b);
 }

 int main() {
     ios::sync_with_stdio(false);
     cin.tie();
     cin >>n;
     while(n--) {
         cin >>p >>q >>b;
         ll g = gcd(p, q);
         p = p / g;
         q = q / g;
         while(g = gcd(q, b), g != ) {
             while(q % g == ) q /= g;
         }
         if(q == ) cout <<"Finite" <<endl;
         else cout <<"Infinite" <<endl;
     }
     return ;
 }

D. XOR-pyramid

time limit per test：2 seconds

memory limit per test：512 megabytes

input：standard input

output：standard output

For an array bb of length mm we define the function ff as

where ⊕⊕ is bitwise exclusive OR.

For example, f(1,2,4,8)=f(1⊕2,2⊕4,4⊕8)=f(3,6,12)=f(3⊕6,6⊕12)=f(5,10)=f(5⊕10)=f(15)=15f(1,2,4,8)=f(1⊕2,2⊕4,4⊕8)=f(3,6,12)=f(3⊕6,6⊕12)=f(5,10)=f(5⊕10)=f(15)=15

You are given an array aa and a few queries. Each query is represented as two integers ll and rr. The answer is the maximum value of ff on all continuous subsegments of the array al,al+1,…,aral,al+1,…,ar.

Input

The first line contains a single integer nn (1≤n≤50001≤n≤5000) — the length of aa.

The second line contains nn integers a1,a2,…,ana1,a2,…,an (0≤ai≤230−10≤ai≤230−1) — the elements of the array.

The third line contains a single integer qq (1≤q≤1000001≤q≤100000) — the number of queries.

Each of the next qq lines contains a query represented as two integers ll, rr (1≤l≤r≤n1≤l≤r≤n).

Output

Print qq lines — the answers for the queries.

Examples

Input

Copy

3
8 4 1
2
2 3
1 2

Output

Copy

5
12

Input

Copy

6
1 2 4 8 16 32
4
1 6
2 5
3 4
1 2

Output

Copy

60
30
12
3

Note

In first sample in both queries the maximum value of the function is reached on the subsegment that is equal to the whole segment.

In second sample, optimal segment for first query are [3,6][3,6], for second query — [2,5][2,5], for third — [3,4][3,4], for fourth — [1,2][1,2].

题意：给你一个序列，然后按照他所给的递推式求出所问区间内f的最大值。

思路：仔细研究一下这个递推式会发现本题的方法为区间dp。由于询问次数太大，因而我们先进行预处理，然后就能在O(1)的复杂度内进行询问。

代码实现如下：

 #include <bits/stdc++.h>
 using namespace std;

 typedef long long ll;
 const int maxn = 5e3 + ;
 int n, q, l, r;
 ll a[maxn], ans[maxn][maxn], dp[maxn][maxn];

 int main() {
     ios::sync_with_stdio(false);
     cin.tie();
     cin >>n;
     for(int i = ; i <= n; i++) {
         cin >>a[i];
         dp[i][i] = a[i];
         ans[i][i] = a[i];
     }
     for(int i = ; i <= n; i++) {
         for(int j = ; j + i <= n; j++) {
             ans[j][j+i] = ans[j][j+i-] ^ ans[j+][i+j];
             dp[j][j+i] = max(ans[j][j+i], max(dp[j][j+i-], dp[j+][i+j]));
         }
     }
     cin >>q;
     while(q--) {
         cin >>l >>r;
         cout <<dp[l][r] <<endl;
     }
     return ;
 }