【bzoj3387-跨栏训练】线段树+dp

我们可以想到一个dp方程：f[i][0]表示当前在i个栅栏的左端点，f[i][1]表示在右端点。

分两种情况：

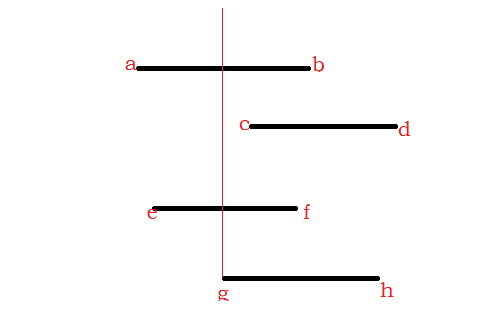
第一种：假设现在要更新线段gh的左端点g，而它下来的路径被ef挡住了，那么必定是有ef来更新g。

为什么呢？因为其它点走到g必定要下落，比如说d到g，就相当于d到f再到g。

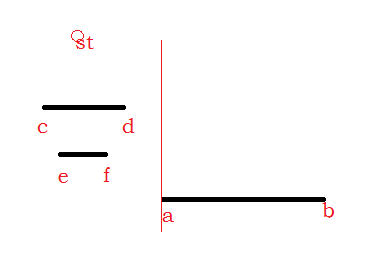
第二种：假设到ab的路径上没有东西挡着，那就可以直接从源点走过去再直接下落。

按照从上到下的顺序插入线段，线段树就是找当前的某个点被哪条id最大（也就是最低的）线段所覆盖。

 #include<cstdio>
 #include<cstdlib>
 #include<cstring>
 #include<iostream>
 #include<ctime>
 #include<queue>
 #include<algorithm>
 using namespace std;

 const int N=**,INF=(int)1e9;
 int n,st,pl,tl,r[N],f[N][];
 struct node{
     int d,id,tmp;
 }p[N];
 struct nd{
     int x1,x2;
 }a[N];
 struct trnode{
     int l,r,lc,rc,id,lazy;
 }t[*N];

 bool cmp_d(node x,node y){return x.d<y.d;}
 int myabs(int x){return x> ? x:-x;}
 int minn(int x,int y){return x<y ? x:y;}
 int maxx(int x,int y){return x>y ? x:y;}

 int bt(int l,int r)
 {
     int x=++tl;
     t[x].l=l;t[x].r=r;
     t[x].lc=t[x].rc=;
     t[x].id=INF;t[x].lazy=INF;
     if(l<r)
     {
         int mid=(l+r)/;
         t[x].lc=bt(l,mid);
         t[x].rc=bt(mid+,r);
     }
     return x;
 }

 void upd(int x)
 {
     if(t[x].lazy==INF) return ;
     int id=t[x].lazy,lc=t[x].lc,rc=t[x].rc;
     t[x].lazy=INF;
     t[x].id=minn(t[x].id,id);
     if(lc) t[lc].lazy=minn(t[lc].lazy,id);
     if(rc) t[rc].lazy=minn(t[rc].lazy,id);
 }

 void change(int x,int l,int r,int id)
 {
     upd(x);
     if(t[x].l==l && t[x].r==r)
     {
         t[x].lazy=minn(t[x].lazy,id);
         upd(x);
         return ;
     }
     int lc=t[x].lc,rc=t[x].rc,mid=(t[x].l+t[x].r)/;
     if(r<=mid) change(lc,l,r,id);
     else if(l>mid) change(rc,l,r,id);
     else
     {
         change(lc,l,mid,id);
         change(rc,mid+,r,id);
     }
 }

 int query(int x,int p)
 {
     upd(x);
     if(t[x].l==t[x].r) return t[x].id;
     int lc=t[x].lc,rc=t[x].rc,mid=(t[x].l+t[x].r)/;
     if(p<=mid) return query(lc,p);
     else return query(rc,p);
 }

 int main()
 {
     // freopen("a.in","r",stdin);
     // freopen("me.out","w",stdout);
     freopen("obstacle.in","r",stdin);
     freopen("obstacle.out","w",stdout);
     scanf("%d%d",&n,&st);
     int x,ed;ed=;pl=;tl=;
     p[++pl].d=st;p[pl].id=n+;
     p[++pl].d=ed;p[pl].id=n+;
     for(int i=;i<=n;i++)
     {
         scanf("%d%d",&a[i].x1,&a[i].x2);
         if(a[i].x1>a[i].x2) swap(a[i].x1,a[i].x2);
         p[++pl].d=a[i].x1;p[pl].id=i;p[pl].tmp=;
         p[++pl].d=a[i].x2;p[pl].id=i;p[pl].tmp=;
     }
     sort(p+,p++pl,cmp_d);
     int mx=;p[].d=INF;
     for(int i=;i<=pl;i++)
     {
         if(p[i].d!=p[i-].d) mx++,r[mx]=p[i].d;
         if(p[i].id==n+) st=mx;
         else if(p[i].id==n+) ed=mx;
         else
         {
             if(p[i].tmp==) a[p[i].id].x1=mx;
             else a[p[i].id].x2=mx;
         }
     }
     bt(,mx);
     change(,st,st,n+);
     a[n+].x1=a[n+].x2=st;
     f[n+][]=f[n+][]=;
     a[].x1=a[].x2=ed;
     for(int i=n;i>=;i--)
     {
         x=query(,a[i].x1);
         if(x<INF) f[i][]=minn(f[x][]+myabs(r[a[x].x1]-r[a[i].x1]),f[x][]+myabs(r[a[x].x2]-r[a[i].x1]));
         else f[i][]=myabs(r[st]-r[a[i].x1]);
         x=query(,a[i].x2);
         if(x<INF) f[i][]=minn(f[x][]+myabs(r[a[x].x1]-r[a[i].x2]),f[x][]+myabs(r[a[x].x2]-r[a[i].x2]));
         else f[i][]=myabs(r[st]-r[a[i].x2]);
         change(,a[i].x1,a[i].x2,i);
     }
     printf("%d\n",f[][]);
     return ;
 }