CF&&CC百套计划1 Codeforces Round #449 C. Willem, Chtholly and Seniorious (Old Driver Tree)

http://codeforces.com/problemset/problem/896/C

题意：

对于一个随机序列，执行以下操作：

区间赋值

区间加

区间求第k小

区间求k次幂的和

对于随机序列，可以使用Old Driver Tree

就是将序列中，连续的相同值域合并为一段

然后暴力操作

#include<set>
#include<vector>
#include<cstdio>
#include<iostream>
#include<algorithm>

using namespace std;

typedef long long LL;

#define N 100001

int n,m,seed,vmax,ret;
int a[N];

struct node
{
    int l,r;
    mutable LL val;
    bool operator < (node p) const
    {
        return l<p.l;
    }
    node(int l=,int r=,LL val=):l(l),r(r),val(val) { }
};

set<node>s;

typedef set<node> :: iterator seti;

vector<pair<LL,int> >par;

void read(int &x)
{
    x=; char c=getchar();
    while(!isdigit(c))  c=getchar();
    while(isdigit(c)) { x=x*+c-''; c=getchar(); }
}

int rnd()
{
    ret=seed;
    seed=((LL)seed*+)%;
    return ret;
}

void split(int pos)
{
    seti it=s.lower_bound(node(pos,-,-));
    if(it==s.end() || it->l>pos)
    {
        --it;
        int l=it->l,r=it->r;
        LL val=it->val;
        s.erase(it);
        s.insert(node(l,pos-,val));
        s.insert(node(pos,r,val));
    }
}

LL quickpow(LL a,LL x,LL mod)
{
    LL res=;
    for(;x;x>>=,a=a*a%mod)
        if(x&) res=res*a%mod;
    return res;
}

int main()
{
    read(n);
    read(m);
    read(seed);
    read(vmax);
    for(int i=;i<=n;++i) a[i]=rnd()%vmax+;
    int r;
    for(int i=;i<=n;)
    {
        r=i+;
        while(a[r]==a[i]) r++;
        s.insert(node(i,r-,(LL)a[i]));
        i=r;
    }
    int op,l,x,y;
    for(int i=;i<=m;++i)
    {
        op=rnd()%+;
        l=rnd()%n+;
        r=rnd()%n+;
        if(l>r) swap(l,r);
        if(op==) x=rnd()%(r-l+)+;
        else x=rnd()%vmax+;
        if(op==) y=rnd()%vmax+;
        split(l);
        if(r<n) split(r+);
        seti itl=s.lower_bound(node(l,-,-));
        seti itr=s.upper_bound(node(r,-,-));
        if(op==)
        {
            for(seti it=itl;it!=itr;++it) it->val+=x;
        }
        else if(op==)
         {
             s.erase(itl,itr);
             s.insert(node(l,r,x));
        }
        else if(op==)
        {
            par.clear();
            for(seti it=itl;it!=itr;++it)
                par.push_back(make_pair(it->val,it->r-it->l+));
            sort(par.begin(),par.end());
            for(int i=;i<par.size();++i)
            {
                x-=par[i].second;
                if(x<=)
                {
                    cout<<par[i].first<<'\n';
                    break;
                }
            }
        }
        else
        {
            LL ans=;
            for(seti it=itl;it!=itr;++it)
            {
                LL val=quickpow(it->val%y,x,y);
                val=val*(it->r-it->l+)%y;
                ans=(ans+val)%y;
            }
            cout<<ans<<'\n';
        }
    }
    return ;
}

C. Willem, Chtholly and Seniorious

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

— Willem...

— What's the matter?

— It seems that there's something wrong with Seniorious...

— I'll have a look...

Seniorious is made by linking special talismans in particular order.

After over 500 years, the carillon is now in bad condition, so Willem decides to examine it thoroughly.

Seniorious has n pieces of talisman. Willem puts them in a line, the i-th of which is an integer ai.

In order to maintain it, Willem needs to perform m operations.

There are four types of operations:

• 1 l r x: For each i such that l ≤ i ≤ r, assign ai + x to ai.
• 2 l r x: For each i such that l ≤ i ≤ r, assign x to ai.
• 3 l r x: Print the x-th smallest number in the index range [l, r], i.e. the element at the x-th position if all the elements ai such thatl ≤ i ≤ r are taken and sorted into an array of non-decreasing integers. It's guaranteed that 1 ≤ x ≤ r - l + 1.
• 4 l r x y: Print the sum of the x-th power of ai such that l ≤ i ≤ r, modulo y, i.e. .

Input

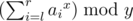The only line contains four integers n, m, seed, vmax (1 ≤ n, m ≤ 105, 0 ≤ seed < 109 + 7, 1 ≤ vmax ≤ 109).

The initial values and operations are generated using following pseudo code:

def rnd():

    ret = seed
    seed = (seed * 7 + 13) mod 1000000007
    return ret

for i = 1 to n:

    a[i] = (rnd() mod vmax) + 1

for i = 1 to m:

    op = (rnd() mod 4) + 1
    l = (rnd() mod n) + 1
    r = (rnd() mod n) + 1

    if (l > r): 
         swap(l, r)

    if (op == 3):
        x = (rnd() mod (r - l + 1)) + 1
    else:
        x = (rnd() mod vmax) + 1

    if (op == 4):
        y = (rnd() mod vmax) + 1

Here op is the type of the operation mentioned in the legend.

Output

For each operation of types 3 or 4, output a line containing the answer.

Examples

input

10 10 7 9

output

2
1
0
3

input

10 10 9 9

output

1
1
3
3

Note

In the first example, the initial array is {8, 9, 7, 2, 3, 1, 5, 6, 4, 8}.

The operations are:

• 2 6 7 9
• 1 3 10 8
• 4 4 6 2 4
• 1 4 5 8
• 2 1 7 1
• 4 7 9 4 4
• 1 2 7 9
• 4 5 8 1 1
• 2 5 7 5
• 4 3 10 8 5