洛谷 P1251 餐巾计划问题（线性规划网络优化）【费用流】

（题外话：心塞...大部分时间都在debug，拆点忘记加N，总边数算错，数据类型标错，字母写错......）

题目链接：https://www.luogu.org/problemnew/show/P1251

洛谷 P1251 餐巾计划问题

输入输出样例

输入样例#1：

3
1 7 5
11 2 2 3 1

输出样例#1：

134

说明

N<=2000

ri<=10000000

p,f,s<=10000

时限4s

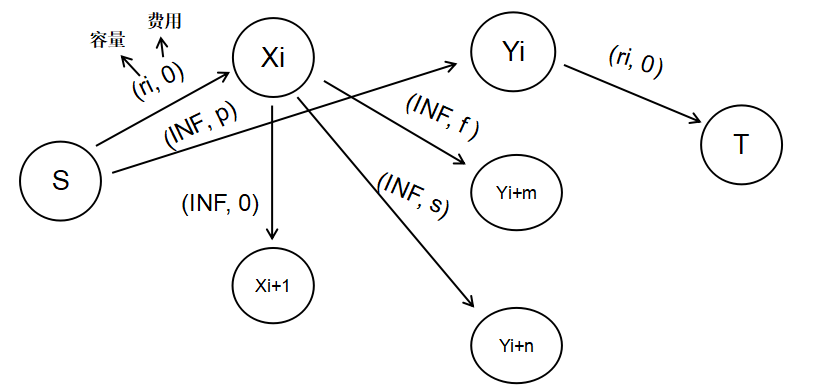
题解：拆点再跑费用流呗，第i天拆成Xi（脏的餐巾）和Yi（干净的餐巾）。对于每天情况，建图示例如下(解释详见代码注释)：

代码：

 #include<bits/stdc++.h>
 using namespace std;
 typedef long long ll;
 const int N = ;
 const int M = ;
 const ll INF = 1e18;
 const int INF2 = 1e9;
 struct Edge { int to,next,cap,flow,cost; }edge[M];
 int head[N],tol;
 int pre[N];
 ll dis[N];
 bool vis[N];
 int V;
 void init(int n) {
     V = n;
     tol = ;
     memset(head,-,sizeof(head));
 }
 void addedge(int u,int v,int cap,int cost) {
     edge[tol].to = v; edge[tol].cap = cap; edge[tol].cost = cost; edge[tol].flow = ; edge[tol].next = head[u]; head[u] = tol++;
     edge[tol].to = u; edge[tol].cap = ; edge[tol].cost = -cost; edge[tol].flow = ; edge[tol].next = head[v]; head[v] = tol++;
 }
 bool spfa(int s,int t) {
     queue<int>q;
     for(int i = ;i < V;i++) {
         dis[i] = INF;
         vis[i] = false;
         pre[i] = -;
     }
     dis[s] = ;
     vis[s] = true;
     q.push(s);
     while(!q.empty()) {
         int u = q.front();
         q.pop();
         vis[u] = false;
         for(int i = head[u]; i != -;i = edge[i].next) {
             int v = edge[i].to;
             if(edge[i].cap > edge[i].flow && dis[v] > dis[u] + edge[i].cost ) {
                 dis[v] = dis[u] + edge[i].cost;
                 pre[v] = i;
                 if(!vis[v]) {
                     vis[v] = true;
                     q.push(v);
                 }
             }
         }
     }
     if(pre[t] == -) return false;
     else return true;
 }
 ll minCostMaxflow(int s,int t,ll &cost) {
     ll flow = ;
     cost = ;
     while(spfa(s,t)) {
         ll Min = INF;
         for(int i = pre[t];i != -;i = pre[edge[i^].to]) {
             if(Min > edge[i].cap - edge[i].flow)
                 Min = edge[i].cap - edge[i].flow;
         }
         for(int i = pre[t];i != -;i = pre[edge[i^].to]) {
             edge[i].flow += Min;
             edge[i^].flow -= Min;
             cost += edge[i].cost * Min;
         }
         flow += Min;
     }
     return flow;
 }
 int main() {
     int n, r, i, j, p, m, f, nn, s;
     ll ans = ;
     scanf("%d", &n);
     init(n*+);
 
     int S = n*+, T = n*+;
 
     for(i = ; i <= n; ++i) {
         scanf("%d", &r);//每天需要餐巾数
         addedge(S, i, r, );
         addedge(i+n, T, r, );
     }
     scanf("%d%d%d%d%d", &p, &m, &f, &nn, &s);
     for(i = ; i <= n; ++i) {
         addedge(S, i+n, INF2, p);//购买新餐巾
         if(i+m<=n) addedge(i, i+m+n, INF2, f);//快洗
         if(i+nn<=n) addedge(i, i+nn+n, INF2, s);//慢洗
         if(i!=n) addedge(i, i+, INF2, );//留到第二天
     }
 
     minCostMaxflow(S, T, ans);
     printf("%lld\n", ans);
     return ;
 }