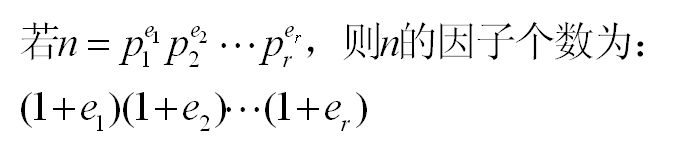zoj 3286 Very Simple Counting---统计[1,N]相同因子个数
Very Simple Counting
Time Limit: 1 Second Memory Limit: 32768 KB
Let f(n) be the number of factors of integer n.
Your task is to count the number of i(1 <= i < n) that makes f(i) = f(n).
Input
One n per line (1 < n <= 1000000).
There are 10000 lines at most.
Output
For each n, output counting result in one line.
Sample Input
4
5
Sample Output
0
2
Hint
f(1) = 1, f(2) = f(3) = f(5) = 2, f(4) = 3.
Author: WU, Jun
Source: ZOJ Monthly, December 2009
理论依据:
zoj的题目,对时间和空间的要求都很高。
这一题,首先做的时候,超时。
不看时间,不看数据,直接枚举,不超时是不可能。
根据的公式和上一题福州大学oj那一题是一样的。
贴一下超时代码吧,留个纪念。
//超时代码 #include<stdio.h>
#include<stdlib.h> int f[];
int Num_Euler(int n)
{
int num=,k,i;
for(i=;i*i<=n;i++)
if(n%i==)
{
k=;
while(n%i==)
{
k++;
n=n/i;
}
num=num*k;
}
if(n!=)
num=num*;
return num;
} void make_ini()
{
int i;
for(i=;i<=;i++)
f[i]=Num_Euler(i);
}
int main()
{
int n,i,num;
make_ini();
while(scanf("%d",&n)>)
{
num=;
for(i=;i<n;i++)
if(f[i]==f[n])
num++;
printf("%d\n",num);
}
return ;
}
后来想用筛选法来筛一次,然后求值。第一次写的时候,也错了。
void make_NumEuler()
{
int i,j,k;
for(i=;i<=;i++)
opl[i]=;
for(i=;i<=len;i++)
for(j=prime[i],k=;j<=;j=j+prime[i],k++)
opl[j]=opl[j]*k;
}
思路是有的,就是没有写出来,(⊙o⊙)…
最后的代码:
#include<iostream>
#include<map>
#include<cstdio>
#include<cstdlib>
#include<cstring> using namespace std; bool s[];
int num[];
int ans[];//个数
int f[];
map<int,int>Q; void make_ini()
{
int i,j,k;
for(i=;i<=;i++)
{
num[i]=i;
ans[i]=;
f[i]=;
}
for(i=;i<=;i++)
if(s[i]==false)//是素数
{
for(j=i;j<=;j=j+i)//枚举每个素数的倍数
{
// if(j%i==0) //这个肯定成立,不需要
{
k=;
while(num[j]%i==)
{
num[j]=num[j]/i;
k++;
}
ans[j]=ans[j]*k;
}
s[j]=true;
}
}
for(i=;i<=;i++)
{
k=ans[i];
if(Q.find(k)==Q.end())
{
Q[k]=;
}
else Q[k]++;
f[i]=Q[k];
}
} int main()
{
int n;
make_ini();
// Q.clear();
while(scanf("%d",&n)>)
{
printf("%d\n",f[n]-);
}
return ;
}
zoj 3286 Very Simple Counting---统计[1,N]相同因子个数的更多相关文章
- Codeforces 11D A Simple Task 统计简单无向图中环的个数(非原创)
太难了,学不会.看了两天都会背了,但是感觉题目稍微变下就不会了.dp还是摸不到路子. 附ac代码: 1 #include<iostream> 2 #include<cstdio> ...
- 17997 Simple Counting 数学
17997 Simple Counting 时间限制:2000MS 内存限制:65535K提交次数:0 通过次数:0 题型: 编程题 语言: 不限定 Description Ly is craz ...
- Javascript 统计复选框选中个数
var checked = document.getElementsByName("checked_c[]"); var checked_counts = 0; for(var i ...
- Linux 统计文件夹下文件个数
查看统计当前目录下文件的个数,包括子目录里的. ls -lR| grep "^-" | wc -l Linux下查看某个目录下的文件.或文件夹个数用到3个命令:ls列目录.用gre ...
- 学c语言做练习之统计文件中字符的个数
统计文件中字符的个数(采用命令行参数) #include<stdio.h> #include<stdlib.h> int main(int argc, char *argv[] ...
- 题目--统计一行文本的单词个数(PTA预习题)
PTA预习题——统计一行文本的单词个数 7-1 统计一行文本的单词个数 (15 分) 本题目要求编写程序统计一行字符中单词的个数.所谓“单词”是指连续不含空格的字符串,各单词之间用空格分隔,空格数可以 ...
- Linux上统计文件夹下文件个数以及目录个数
对于linux终端用户而言,统计文件夹下文件的多少是经常要做的操作,于我而言,我会经常在谷歌搜索一个命令,“如何在linux统计文件夹的个数”,然后点击自己想要的答案,但是有时候不知道统计文件夹命令运 ...
- 统计无向图中三角形的个数,复杂度m*sqrt(m).
统计无向图中三角形的个数,复杂度m*sqrt(m). #include<stdio.h> #include<vector> #include<set> #inclu ...
- 给出一个string字符串,统计里面出现的字符个数
给出一个string字符串,统计里面出现的字符个数 解决方案: 使用algorithm里面的count函数,使用方法是count(begin,end,'c'),其中begin指的是起始地址,end指的 ...
随机推荐
- Android 日常总结的一些方法使用
1. setImageResource : 更改图片的资源 2. setClickable : 设置为true时,表明控件可以点击,如果为false,就不能点击 . 注意,setOnClickLi ...
- Python3.5 学习十
多进程: 多线程和多进程的区别: Python多线程不适合CPU操作密集型的任务,适合IO操作密集型的任务(IO操作不占用CPU) Python折中解决多线程不能真正同步运算的方案是:起多个进程,每个 ...
- docker和定时任务
查看linux信息 cat /etc/issue 以id运行容器docker start 1c3339d7f9a8通过id结束容器 docker kill 1c3339d7f9a8 Ubuntu 安装 ...
- Golang channel 的基本使用方法
package main import ( "fmt" "learner/Add" "time" ) //a. 普通类型,普通变量保存的就是 ...
- sublime text 内调试Javascript代码
转自:sublime内调试Javascript代码 之前用webstorm, 可以直接调试js, 在浏览器中也可以调试js,最近换了sublime text, 在想它是否支持调试js代码,于是找到了这 ...
- dataTable 参数说明
下面是一些常用的参数列表,比较常用或者有价值的标示为绿色. 功能参数(Features) 参数名 说明 参考值 默认值 autoWidth 定义是否由控件自动控制列宽 Boolean true def ...
- uiautomatorviewer 双击闪退问题解决
最近在学习app自动测试,结果在打开uiautomatorviewer查看app界面元素时,就出现了闪退的问题,找了很多很多方法,最后终于可以解决了,详情请继续往下看 首次安装adt的步骤 将下载的压 ...
- 如何解决jade标签没有闭合,如input
最近用jade模板引擎编写html时发现input编译输出为<input>,而我想要的效果为<input/>, 如何解决呢,这时我们可以这样写: input/ ---& ...
- gitHub-高仿58同城加载动画
导入方式: /build.gradle repositories { maven { url "https://jitpack.io" } } /app/build.gradle ...
- win7,8走网络打印机出现删除设备和打印机门未关闭的解决方法
不多说,直接上干货! 用学校的内网连接, 即可. 右键,查看设备网页. 出现下面的情况: 多学学. 欢迎大家,加入我的微信公众号:大数据躺过的坑 人工智能躺过的坑 同时,大家 ...