图-最小生成树算法之Kruskal及其Java实现

1.Kruskal算法

Kruskal算法基于贪心，因此它追求的是近似最优解，也就是说由Kruskal得出的生成树并不一定是最优解。

Kruskal算法求最小生成树的关键在于，每次选取图中权值最小（及贪心），并不会构成环的边，直到所有点都被囊括。一般，边的个数=点的个数-1。

如下无向图：

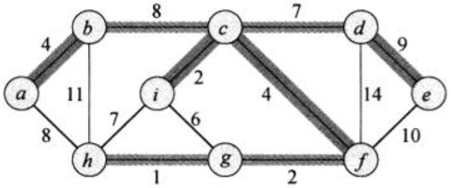要找到最小生成树，克鲁斯卡尔算法的步骤如下：

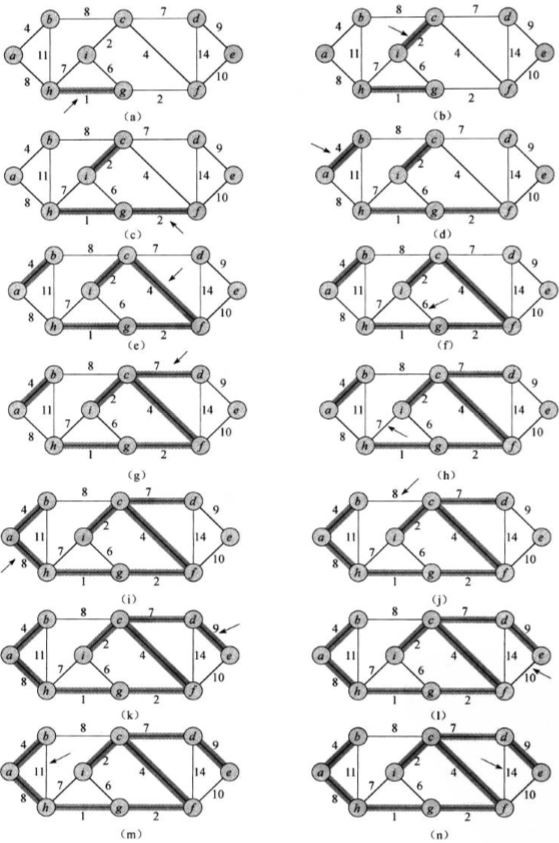
2.Java实现

针对上述《算法导论》中的例子，有Java代码如下：

 import java.util.ArrayList;
 import java.util.Collections;
 import java.util.Iterator;

 //图类 无向图
 class G{
     ArrayList<V> vs=new ArrayList<V>();
     ArrayList<E> es=new ArrayList<E>();

     public void addV(V v) {
         vs.add(v);
     }

     public void add(E e) {
         es.add(e);
     }
 }

 //点
 class V{
     String name;
     boolean isvisited=false;

     public V(String name) {
         this.name=name;
     }

     @Override
     public String toString() {
         return name;
     }
 }

 //边
 class E{
     V v1;   //点
     V v2;   //点
     int Weight;   //权重
     boolean isvisited=false;

     public E(V v1,V v2,int Weight) {
         this.v1=v1;
         this.v2=v2;
         this.Weight=Weight;
     }

     @Override
     public String toString() {
         return "(" + v1 + ", " + v2 + ":" + Weight + ")";
     }
 }

 public class MinTree {
     //克鲁斯卡尔
     static void kruskal(G graph) {
         ArrayList<E> edges=graph.es;  //存储图的边集合
         ArrayList<E> forest=new ArrayList<E>();  //存放符合结果的边

         for(E e:edges) {   //遍历边集合，在初始化图的时候，边已按照权值排序
             ArrayList<E> testForest=refreshForest(forest);
             getEnd(testForest,e.v1,e.v2);
             if(endV) {  //判断是否形成回路
                 System.out.print(e);    //输出符合条件（不形成回路，权值最小）的边
                 forest.add(e);
             }
         }
     }

     //将图的边集合按权值排序
     static ArrayList<E> sortEdgeByWeight(ArrayList<E> es){
         for(int i=0;i<es.size();i++) {
             for(int j=0;j<es.size();j++) {
                 if(es.get(i).Weight<es.get(j).Weight) {
                     Collections.swap(es, i, j);
                 }
             }
         }
         return es;
     }

     static boolean endV=true;
     //判断新的边是否会和已有森林形成环：即得到目标点的末节点，由此判断两者是否相同，若相同则有环
     static void getEnd(ArrayList<E> testForest,V start,V end) {
         for(E e:testForest) {
             if(e.isvisited==false) {
                 if(e.v1.equals(start)) {
                     e.isvisited=true;
                     if(e.v2.equals(end)) {
                         endV=false;
                     }else {
                         getEnd(testForest,e.v2,end);
                     }
                 }else if (e.v2.equals(start)) {
                     e.isvisited=true;
                     if(e.v1.equals(end)) {
                         endV=false;
                     }else {
                         getEnd(testForest,e.v1,end);
                     }
                 }
             }
         }
     }

     //刷新森林：将森林中所有边标为未被查看，将endV标志也初始化一下
     static ArrayList<E> refreshForest(ArrayList<E> forest) {
         endV=true;
         for(E e:forest) {
             e.isvisited=false;
         }
         return forest;
     }

     public static void main(String[] args) {
         // TODO Auto-generated method stub
         //创建点
         V a=new V("a");
         V b=new V("b");
         V c=new V("c");
         V d=new V("d");
         V e=new V("e");
         V f=new V("f");
         V g=new V("g");
         V h=new V("h");
         V i=new V("i");
         //创建点

         //创建边
         E e0=new E(a,b,4);
         E e1=new E(a,h,8);
         E e2=new E(b,h,11);
         E e3=new E(b,c,8);
         E e4=new E(h,i,7);
         E e5=new E(h,g,1);
         E e6=new E(i,c,2);
         E e7=new E(i,g,6);
         E e8=new E(c,d,7);
         E e9=new E(c,f,4);
         E e10=new E(g,f,2);
         E e11=new E(d,f,14);
         E e12=new E(d,e,9);
         E e13=new E(f,e,10);
         //创建边

         //创建图
         G graph=new G();
         graph.addV(a);
         graph.addV(b);
         graph.addV(c);
         graph.addV(d);
         graph.addV(e);
         graph.addV(f);
         graph.addV(g);
         graph.addV(h);
         graph.addV(i);
         ArrayList<E> es=new ArrayList<E>();
         es.add(e0);
         es.add(e1);
         es.add(e2);
         es.add(e3);
         es.add(e4);
         es.add(e5);
         es.add(e6);
         es.add(e7);
         es.add(e8);
         es.add(e9);
         es.add(e10);
         es.add(e11);
         es.add(e12);
         es.add(e13);
         graph.es=sortEdgeByWeight(es);
         //创建图

         //输出图
         ArrayList<V> vertexs=graph.vs;
         ArrayList<E> edges=graph.es;
         Iterator iVertex=vertexs.iterator();
         Iterator iEdge=edges.iterator();
         System.out.println("点集合：");
         while(iVertex.hasNext()) {
             System.out.print(iVertex.next());
         }
         System.out.println();
         System.out.println("边集合：");
         while(iEdge.hasNext()) {
             System.out.print(iEdge.next());
         }
         //输出图

         //最小生成树
         //克鲁斯卡尔
         System.out.println("");
         System.out.println("克鲁斯卡尔：");
         kruskal(graph);
         //最小生成树

     }

 }

输出：