bzoj2111ZJ2010排列计数_solution

　　　　　　　　　　-by bzoj

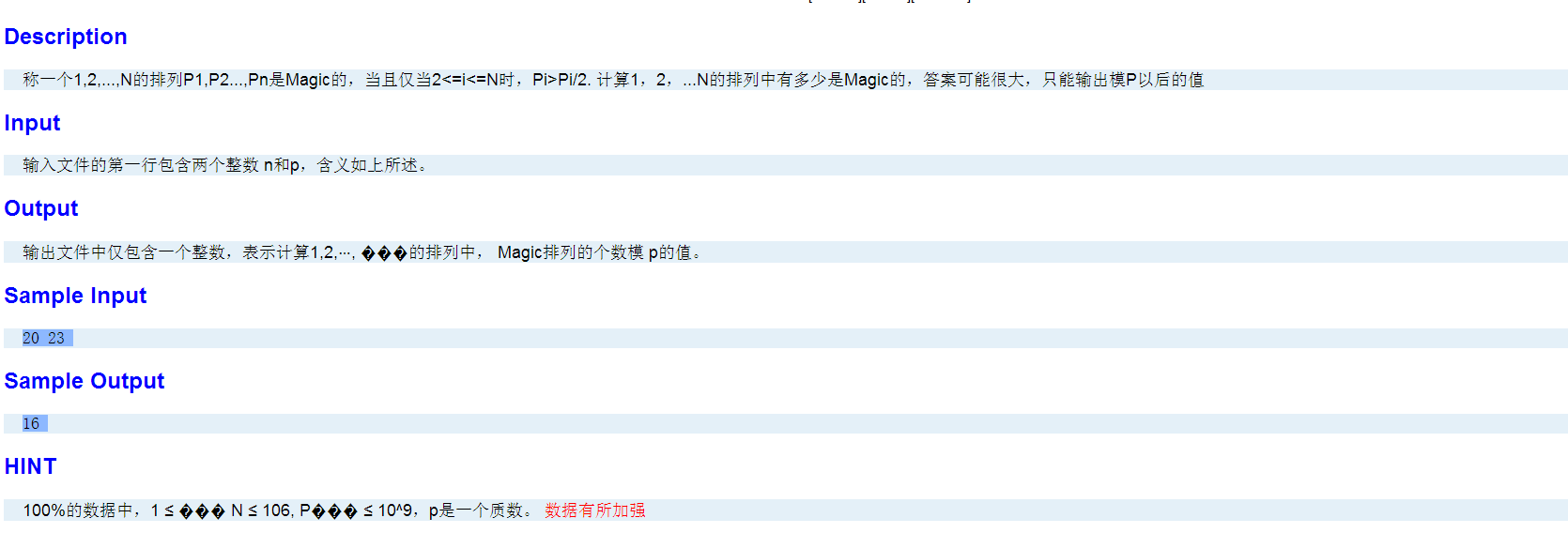
http://www.lydsy.com/JudgeOnline/problem.php?id=2111

---

---

考虑第i个位置上的数字的可能性只取决于第i/2位置上的数，以及剩余数集的大小，可以看出一个树形模型

考虑第i个位置上的数字只会影响第i*2与i*2+1两个位置的可能性，发现这是个二叉树（完全二叉树）

而且是类似小根堆的形式，于是这个树的形态固定，第1个位置上只能放1；

这启发我们进一步思考

对根（第1个位置）来说，他自己是数集中最小的那个，从剩下n-1个数字中，挑一些填满左子树的节点，剩下填右子树，由于只有数字的个数影响结果，所以对左右子树的填法可以看做一个类似的子问题递归进行；

于是有f[i]=C(sum[i<<1],sum[i<<1]+sum[i<<1|1])*f[i<<1]*f[i<<1|1];

C为组合数；

注意组合数的处理细节

O(nlogn);

代码：

#include<cstdio>
#define LL long long
using namespace std;
int N;
LL P;
int sum[];
LL inv[];
LL Sqr(LL ,int );
void dfs(int );
LL dp(int );
LL C(int ,int );
int main()
{
    int i,j,k;
    scanf("%lld%lld",&N,&P);
    for(i=;i<=N;i++)
        inv[i]=Sqr(i%P,P-);
    dfs();
    printf("%lld",dp());
    return ;
}
LL Sqr(LL x,int n){
    LL ret=;
    while(n){
        if(n&)
            (ret*=x)%=P;
        (x*=x)%=P,n>>=;
    }
    return ret;
}
void dfs(int x){
    if((x<<)<=N)
        dfs(x<<);
    if((x<<|)<=N)
        dfs(x<<|);
    sum[x]=sum[x<<]+sum[x<<|]+;
}
LL dp(int x){
    LL a=,b=,ret=;
    if((x<<)<=N)
        a=dp(x<<);
    if((x<<|)<=N)
        b=dp(x<<|);
    ret=a*b%P;(ret*=C(sum[x<<],sum[x<<]+sum[x<<|]))%=P;
    return ret;
}
LL C(int m,int n){
    int i,j=;
    LL ret=;
    for(i=;i<=m;i++)
        if((n-i+)%P!=&&i%P!=)
            (ret*=(((n-i+1ll)*inv[i])%P))%=P;
        else
            j+=((n-i+)%P==?:)+(i%P==?-:);
    return  j>?0ll:ret;
}