KMP算法之next数组的求解思路

2.next数组的求解思路

本部分内容转自：http://www.ruanyifeng.com/blog/2013/05/Knuth%E2%80%93Morris%E2%80%93Pratt_algorithm.html

　　通过上文完全可以对kmp算法的原理有个清晰的了解，那么下一步就是编程实现了，其中最重要的就是如何根据待匹配的模版字符串求出对应每一位的最大相同前后缀的长度。我先给出我的代码：

 1 void makeNext(const char P[],int next[])
 2 {
 3     int q,k;//q:模版字符串下标；k:最大前后缀长度
 4     int m = strlen(P);//模版字符串长度
 5     next[0] = 0;//模版字符串的第一个字符的最大前后缀长度为0
 6     for (q = 1,k = 0; q < m; ++q)//for循环，从第二个字符开始，依次计算每一个字符对应的next值
 7     {
 8         while(k > 0 && P[q] != P[k])//递归的求出P[0]···P[q]的最大的相同的前后缀长度k
 9             k = next[k-1];          //不理解没关系看下面的分析，这个while循环是整段代码的精髓所在，确实不好理解
10         if (P[q] == P[k])//如果相等，那么最大相同前后缀长度加1
11         {
12             k++;
13         }
14         next[q] = k;
15     }
16 } 

　　现在我着重讲解一下while循环所做的工作：

1. 　　已知前一步计算时最大相同的前后缀长度为k（k>0），即P[0]···P[k-1]；
2. 　　此时比较第k项P[k]与P[q],如图1所示
3. 　　如果P[K]等于P[q]，那么很简单跳出while循环;
4. 　　关键！关键有木有！关键如果不等呢？？？那么我们应该利用已经得到的next[0]···next[k-1]来求P[0]···P[k-1]这个子串中最大相同前后缀，可能有同学要问了——为什么要求P[0]···P[k-1]的最大相同前后缀呢？？？是啊！为什么呢？ 原因在于P[k]已经和P[q]失配了，而且P[q-k] ··· P[q-1]又与P[0] ···P[k-1]相同，看来P[0]···P[k-1]这么长的子串是用不了了，那么我要找个同样也是P[0]打头、P[k-1]结尾的子串即P[0]···P[j-1](j==next[k-1])，看看它的下一项P[j]是否能和P[q]匹配。如图2所示

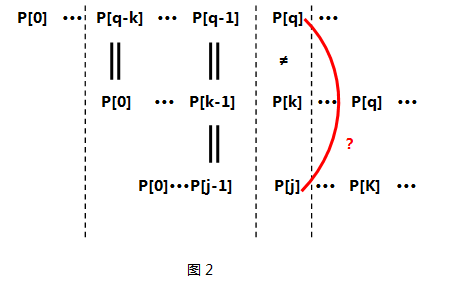
附代码：

 1 #include<stdio.h>
 2 #include<string.h>
 3 void makeNext(const char P[],int next[])
 4 {
 5     int q,k;
 6     int m = strlen(P);
 7     next[0] = 0;
 8     for (q = 1,k = 0; q < m; ++q)
 9     {
10         while(k > 0 && P[q] != P[k])
11             k = next[k-1];
12         if (P[q] == P[k])
13         {
14             k++;
15         }
16         next[q] = k;
17     }
18 }
19
20 int kmp(const char T[],const char P[],int next[])
21 {
22     int n,m;
23     int i,q;
24     n = strlen(T);
25     m = strlen(P);
26     makeNext(P,next);
27     for (i = 0,q = 0; i < n; ++i)
28     {
29         while(q > 0 && P[q] != T[i])
30             q = next[q-1];
31         if (P[q] == T[i])
32         {
33             q++;
34         }
35         if (q == m)
36         {
37             printf("Pattern occurs with shift:%d\n",(i-m+1));
38         }
39     }
40 }
41
42 int main()
43 {
44     int i;
45     int next[20]={0};
46     char T[] = "ababxbababcadfdsss";
47     char P[] = "abcdabd";
48     printf("%s\n",T);
49     printf("%s\n",P );
50     // makeNext(P,next);
51     kmp(T,P,next);
52     for (i = 0; i < strlen(P); ++i)
53     {
54         printf("%d ",next[i]);
55     }
56     printf("\n");
57
58     return 0;
59 }