2016CCPC东北地区大学生程序设计竞赛 （2018年8月22日组队训练赛）
A题题目：
题意：
生成一棵最小生成树，边权值为两个节点的最小公倍数。
思路：
由最小公倍数的和最大公约数的关系：lcm(a, b) = a * b / gcd(a, b)知，我们要使这棵树边权之和尽可能小，那么就要使的等号右边尽可能小，由于b是固定的（从1遍历到n），那么就只能使a / gcd(a,b)尽可能小。又因为我们知道任何数与1的最大公约数为1，且1/1=1，此时是lcm(a, b)是最小值（毕竟lcm(a, b)不可能为0嘛。
综上所述，将2~n都与1相连时所得到的结果最小。此时结果为
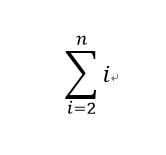
代码实现如下：
#include <set>
#include <map>
#include <queue>
#include <stack>
#include <cmath>
#include <bitset>
#include <cstdio>
#include <string>
#include <vector>
#include <cstdlib>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std; typedef long long LL;
typedef pair<LL, LL> pLL;
typedef pair<LL, int> pli;
typedef pair<int, LL> pil;;
typedef pair<int, int> pii;
typedef unsigned long long uLL; #define lson i<<1
#define rson i<<1|1
#define lowbit(x) x&(-x)
#define bug printf("*********\n");
#define debug(x) cout<<"["<<x<<"]" <<endl;
#define FIN freopen("D://code//in.txt", "r", stdin);
#define IO ios::sync_with_stdio(false),cin.tie(0); const double eps = 1e-;
const int mod = 1e9 + ;
const int maxn = + ;
const double pi = acos(-);
const int inf = 0x3f3f3f3f;
const LL INF = 0x3f3f3f3f3f3f3f3f; int t, n; int main() {
int icase = ;
scanf("%d", &t);
while(t--) {
scanf("%d", &n);
printf("Case #%d: %lld\n", ++icase, (LL) (n + ) * (n - ) / );
}
return ;
}
B题题目：
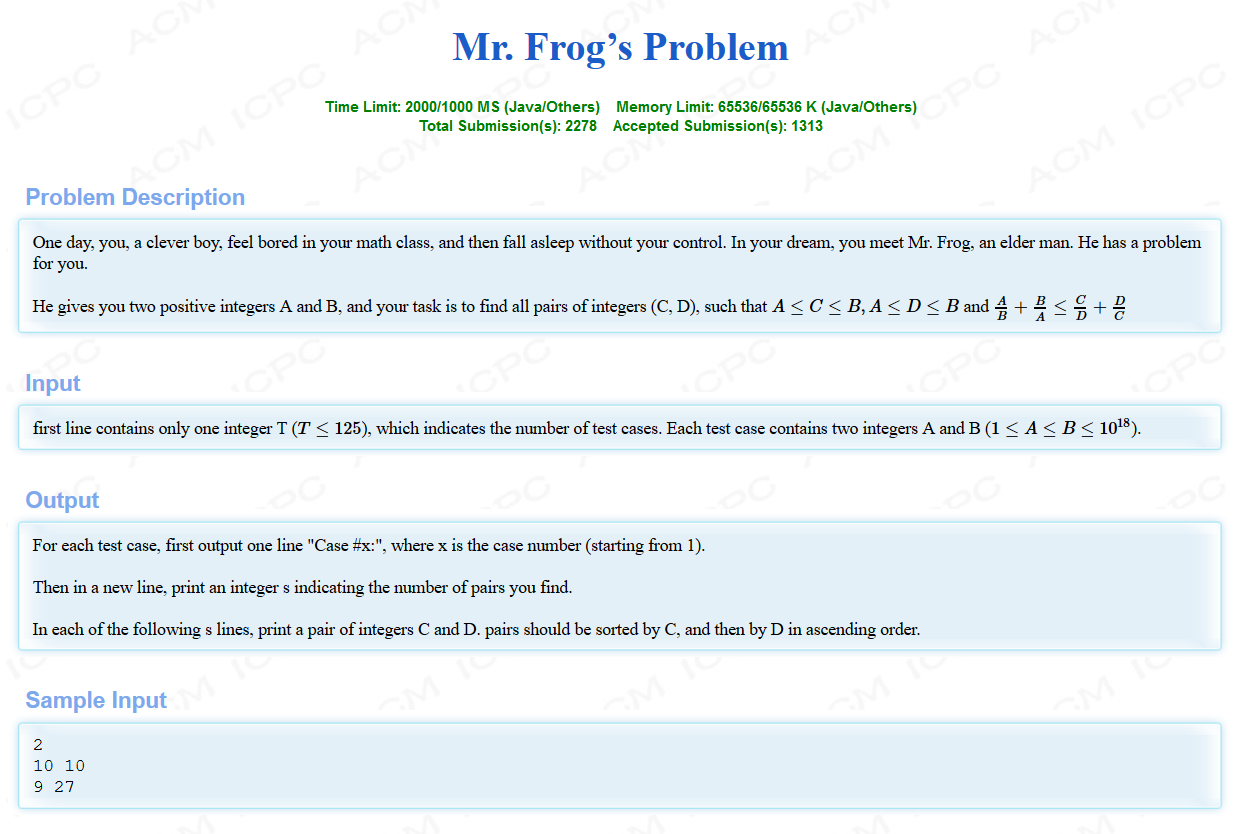
题意：
给你A,B，让你找到所有满足A <= C <= B,A <= D <= B使得A / B + B / A <= C / D + D / C.
思路：
对于本题我们通过证明得到当C=A，D=B或D=A,C=B时才满足题目要求，证明如下：
代码实现如下：
#include <set>
#include <map>
#include <queue>
#include <stack>
#include <cmath>
#include <bitset>
#include <cstdio>
#include <string>
#include <vector>
#include <cstdlib>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std; typedef long long LL;
typedef pair<LL, LL> pLL;
typedef pair<LL, int> pli;
typedef pair<int, LL> pil;;
typedef pair<int, int> pii;
typedef unsigned long long uLL; #define lson i<<1
#define rson i<<1|1
#define lowbit(x) x&(-x)
#define bug printf("*********\n");
#define debug(x) cout<<"["<<x<<"]" <<endl;
#define FIN freopen("D://code//in.txt", "r", stdin);
#define IO ios::sync_with_stdio(false),cin.tie(0); const double eps = 1e-;
const int mod = 1e9 + ;
const int maxn = + ;
const double pi = acos(-);
const int inf = 0x3f3f3f3f;
const LL INF = 0x3f3f3f3f3f3f3f3f; int t;
LL a, b; int main() {
int icase = ;
scanf("%d", &t);
while(t--) {
scanf("%lld %lld", &a, &b);
printf("Case #%d:\n", ++icase);
if(a == b) printf("1\n%lld %lld\n", a, b);
else printf("2\n%lld %lld\n%lld %lld\n", a, b, b, a);
}
return ;
}
E题题目：
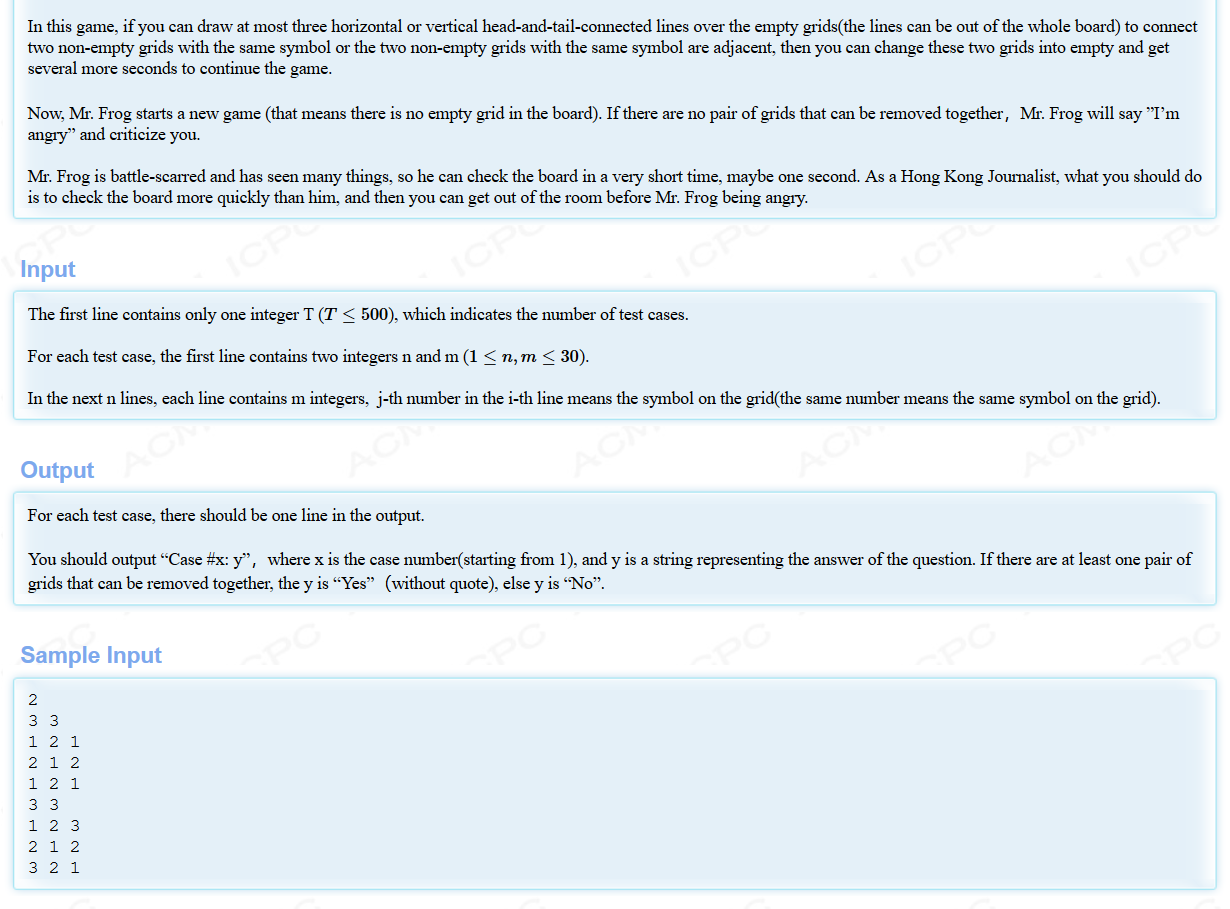
题意：
童年时的连连看~本题需要判断的是你第一步是否能够消掉一对相同的数，本题的消除条件为两个相同的数相连，或者两个相同的数在同一个边界（不可以第一行与第一列进行消除）。
思路：
直接进行模拟即可。
代码实现如下：
#include <set>
#include <map>
#include <queue>
#include <stack>
#include <cmath>
#include <bitset>
#include <cstdio>
#include <string>
#include <vector>
#include <cstdlib>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std; typedef long long LL;
typedef pair<LL, LL> pLL;
typedef pair<LL, int> pli;
typedef pair<int, LL> pil;;
typedef pair<int, int> pii;
typedef unsigned long long uLL; #define lson i<<1
#define rson i<<1|1
#define lowbit(x) x&(-x)
#define bug printf("*********\n");
#define debug(x) cout<<"["<<x<<"]" <<endl;
#define FIN freopen("D://code//in.txt", "r", stdin);
#define IO ios::sync_with_stdio(false),cin.tie(0); const double eps = 1e-;
const int mod = 1e9 + ;
const int maxn = + ;
const double pi = acos(-);
const int inf = 0x3f3f3f3f;
const LL INF = 0x3f3f3f3f3f3f3f3f; int t, n, m;
int mp[][], vis[][]; bool check() {
for(int i = ; i < n; i++) {
for(int j = ; j < m; j++) {
if(mp[i][j] == mp[i][j-]) return true;
}
}
for(int j = ; j < m; j++) {
for(int i = ; i < n; i++) {
if(mp[i][j] == mp[i-][j]) return true;
}
}
return false;
} int main() {
scanf("%d", &t);
int icase = ;
while(t--) {
memset(vis, , sizeof(vis));
scanf("%d%d", &n, &m);
for(int i = ; i < n; i++) {
for(int j = ; j < m; j++) {
scanf("%d", &mp[i][j]);
}
}
int flag = ;
for(int i = ; i < m; i++) {
vis[][mp[][i]]++;
vis[][mp[n-][i]]++;
if(vis[][mp[][i]] >= || vis[][mp[n-][i]] >= ) {
flag = ;
}
}
for(int i = ; i < n; i++) {
vis[][mp[i][]]++;
vis[][mp[i][m-]]++;
if(vis[][mp[i][]] >= || vis[][mp[i][m-]] >= ) {
flag = ;
}
}
if(check()) {
flag = ;
}
if(flag) printf("Case #%d: Yes\n", ++icase);
else printf("Case #%d: No\n", ++icase);
}
return ;
}
F题题面：
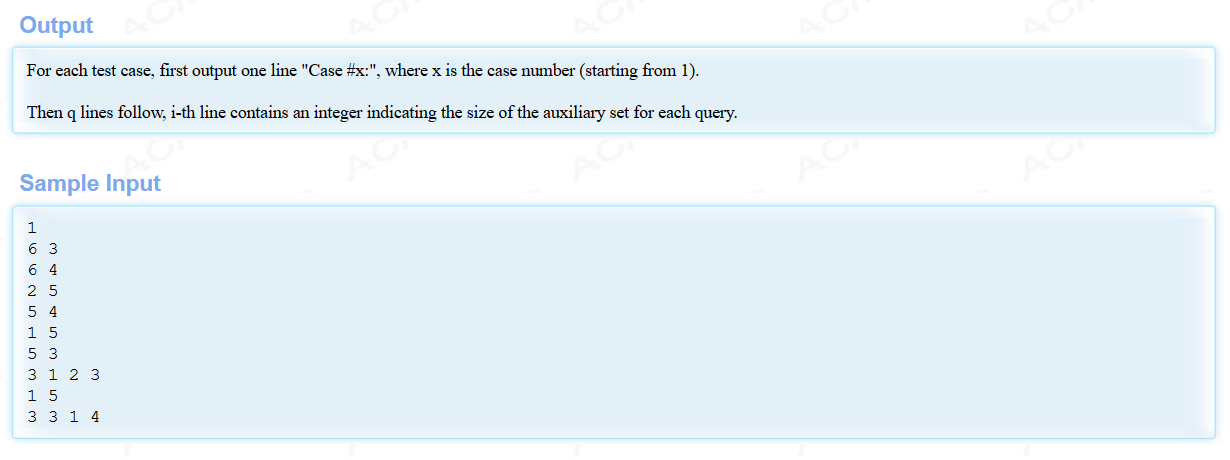
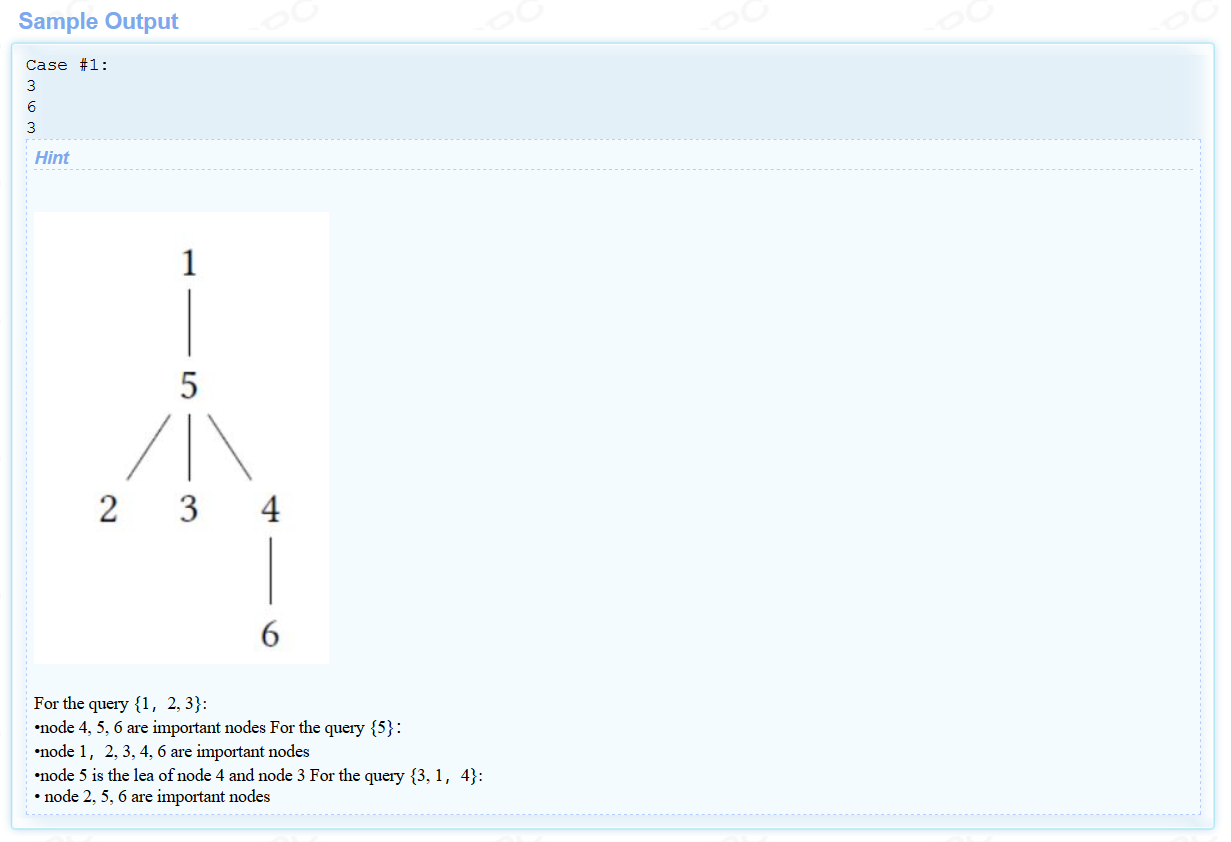
题意：
给你一棵有n个节点的树，有q次查询，每次查询告诉你k个不重要的点的编号，要求你统计：
1.重要节点的个数；
2.是两个重要节点的LCA的节点个数。
上述两种统计的节点不会重复。
思路：
本题初看会以为需要求LCA，但是很显然这么大的数据，如果求LCA的话妥妥的T，因此我们得换个思路。
我们知道对于节点u，如果它的至少有两个子节点（互不相同）的子孙节点有重要节点，那么这个节点就一定满足第二个条件。
因此我们对于每次查询，我们先将这k个数按照他们的深度进行排序，如果某一个不重要它的子节点中没有重要节点，那么这个节点就不用考虑，且相当于父亲节点少了一个子节点；当它的子节点中的重要节点数大于等于2，那么这个节点需要进行统计，且它的父亲节点不需要减少子节点。
代码实现如下：
#include <set>
#include <map>
#include <queue>
#include <stack>
#include <cmath>
#include <bitset>
#include <cstdio>
#include <string>
#include <vector>
#include <cstdlib>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std; typedef long long LL;
typedef pair<LL, LL> pLL;
typedef pair<LL, int> pli;
typedef pair<int, LL> pil;;
typedef pair<int, int> pii;
typedef unsigned long long uLL; #define lson i<<1
#define rson i<<1|1
#define lowbit(x) x&(-x)
#define bug printf("*********\n");
#define debug(x) cout<<"["<<x<<"]" <<endl;
#define FIN freopen("D://code//in.txt", "r", stdin);
#define IO ios::sync_with_stdio(false),cin.tie(0); const double eps = 1e-;
const int mod = 1e9 + ;
const int maxn = + ;
const double pi = acos(-);
const int inf = 0x3f3f3f3f;
const LL INF = 0x3f3f3f3f3f3f3f3f; int t, n, q, u, v, tot, k, ans;
int num[maxn], sz[maxn], vis[maxn], head[maxn];
int fa[maxn],dep[maxn],cnt[maxn]; struct Edge {
int v, next;
}ed[maxn<<]; void init() {
tot = ;
for(int i = ; i < maxn; i++) fa[i] = i;
memset(sz, , sizeof(sz));
memset(vis, , sizeof(vis));
memset(head, -, sizeof(head));
} void addedge(int u, int v) {
ed[tot].v = v;
ed[tot].next = head[u];
head[u] = tot++;
ed[tot].v = u;
ed[tot].next = head[v];
head[v] = tot++;
} void dfs(int u, int p,int d) {
sz[u] = ;
fa[u] = p;
dep[u] = d;
for(int i = head[u]; ~i; i = ed[i].next) {
int v = ed[i].v;
if(v != p) {
sz[u]++;
dfs(v, u, d+);
}
}
} struct node {
int v,dep;
}qu[maxn]; int cmp(node a,node b){
return a.dep>b.dep;
} int main() {
scanf("%d", &t);
int icase = ;
while(t--) {
scanf("%d%d", &n, &q);
init();
for(int i = ; i < n; i++) {
scanf("%d%d", &u, & v);
addedge(u, v);
}
dfs(, ,);
printf("Case #%d:\n", ++icase);
while(q--) {
scanf("%d", &k);
ans = n - k;
for(int i = ; i <= k; i++) {
scanf("%d", &qu[i].v);
qu[i].dep = dep[qu[i].v];
}
sort(qu+,qu++k,cmp);
for (int i = ; i <= k; i++) {
if (sz[qu[i].v] - vis[qu[i].v] >= ) ans++;
else if (sz[qu[i].v] - vis[qu[i].v] == ) vis[fa[qu[i].v]]++;
}
for(int i = ; i <= k; i++) {
vis[qu[i].v] = ;
vis[fa[qu[i].v]] = ;
}
printf("%d\n", ans);
}
}
return ;
}
H题题目：
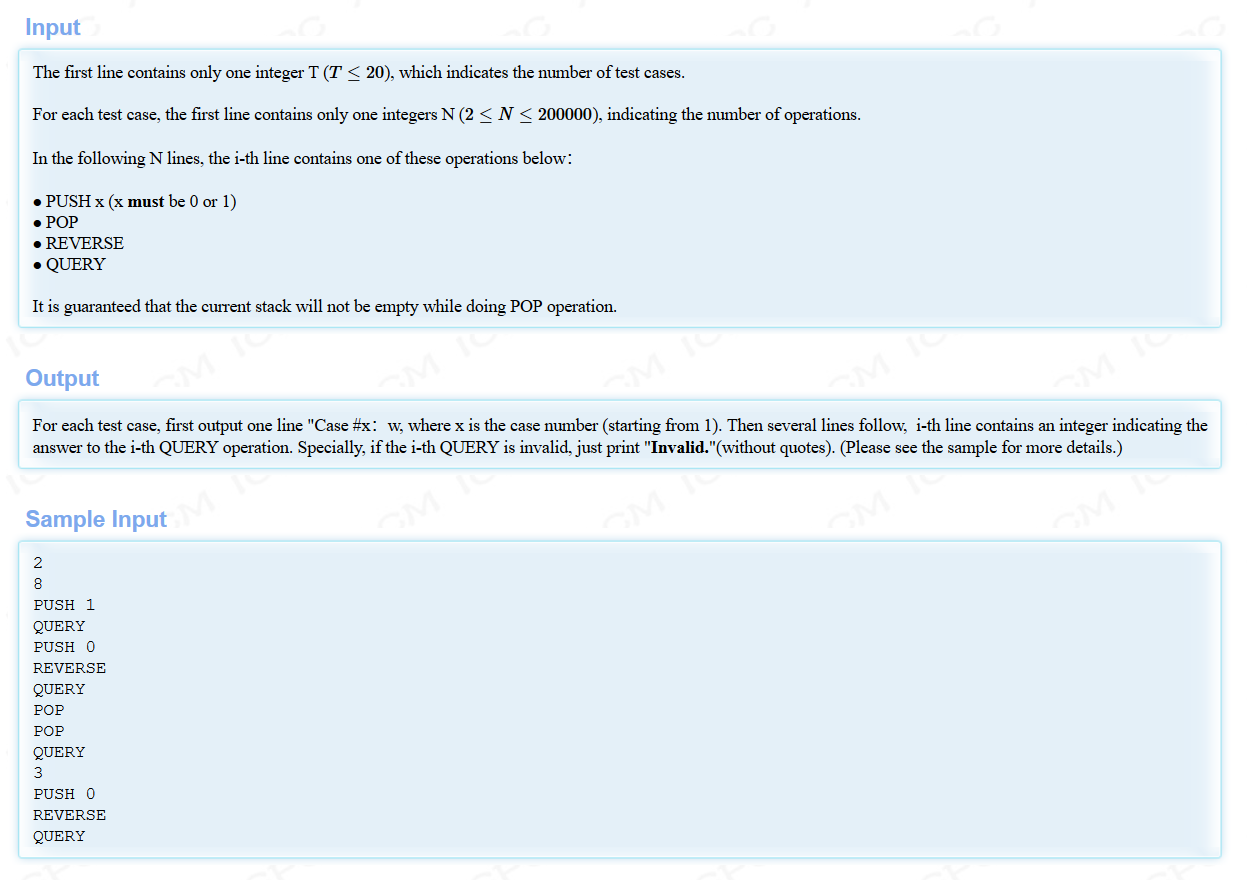
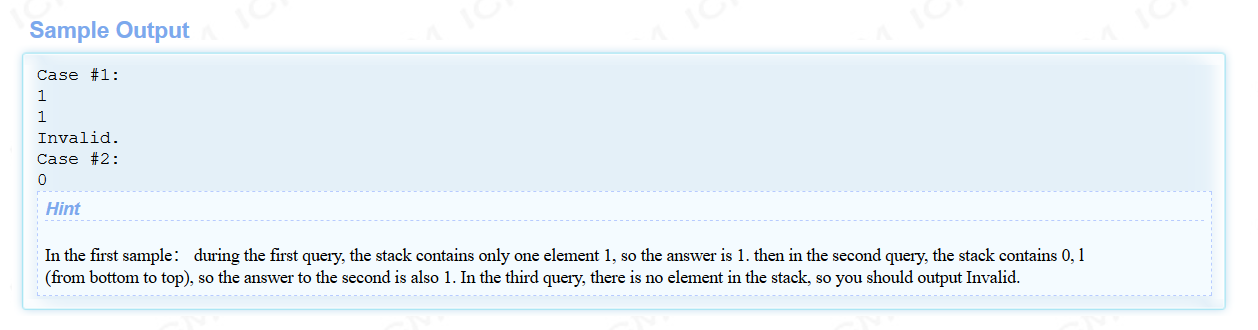
题意：
模拟栈。
思路：
直接模拟即可，对于每次query，我们可以通过找规律发现，只需统计当前栈栈底第一个0下方有多少个1，因为当1上方有0，且0上面有数，那么0及其上方的数进行操作后一定为1，然后对于下方的1奇偶进行讨论即可，具体情况请看代码。
代码实现如下：
#include <set>
#include <map>
#include <queue>
#include <stack>
#include <cmath>
#include <bitset>
#include <cstdio>
#include <string>
#include <vector>
#include <cstdlib>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std; typedef long long LL;
typedef pair<LL, LL> pLL;
typedef pair<LL, int> pli;
typedef pair<int, LL> pil;;
typedef pair<int, int> pii;
typedef unsigned long long uLL; #define lson i<<1
#define rson i<<1|1
#define lowbit(x) x&(-x)
#define bug printf("*********\n");
#define debug(x) cout<<"["<<x<<"]" <<endl;
#define FIN freopen("D://code//in.txt", "r", stdin);
#define IO ios::sync_with_stdio(false),cin.tie(0); const double eps = 1e-;
const int mod = 1e9 + ;
const int maxn = + ;
const double pi = acos(-);
const int inf = 0x3f3f3f3f;
const LL INF = 0x3f3f3f3f3f3f3f3f; int t, n;
char s[];
int a[];
multiset<int> st;
multiset<int>::iterator it; void solve() {
int nw = , l = , r = , sz = ;
while(n--) {
scanf("%s", s);
if(s[] == 'S') {
int x;
sz++;
scanf("%d", &x);
if(nw & ) {
a[--l] = x;
if(x == ) st.insert(l);
} else {
if(x == ) st.insert(r);
a[r++] = x;
}
} else if(s[] == 'P') {
if(l == r) continue;
sz--;
if(nw & ) {
st.erase(l);
l++;
} else {
r--;
st.erase(r);
}
} else if(s[] == 'V') {
nw++;
} else {
if(l == r) {
printf("Invalid.\n");
continue;
}
if(r-l == ) {
printf("%d\n", a[l]);
continue;
}
int sum;
if(st.empty()) {
sum = r - l;
if(sum & ) printf("1\n");
else printf("0\n");
} else {
if(nw & ) {
int k = *--st.end();
sum = r - k - ;
} else {
int k = *st.begin();
sum = k - l;
}
if(sum == sz - ) {
if(sum & ) printf("1\n");
else printf("0\n");
} else {
if(sum & ) printf("0\n");
else printf("1\n");
}
}
}
}
} int main() {
//FIN;
int icase = ;
scanf("%d", &t);
while(t--) {
st.clear();
printf("Case #%d:\n", ++icase);
scanf("%d", &n);
solve();
}
return ;
}
J题题目：
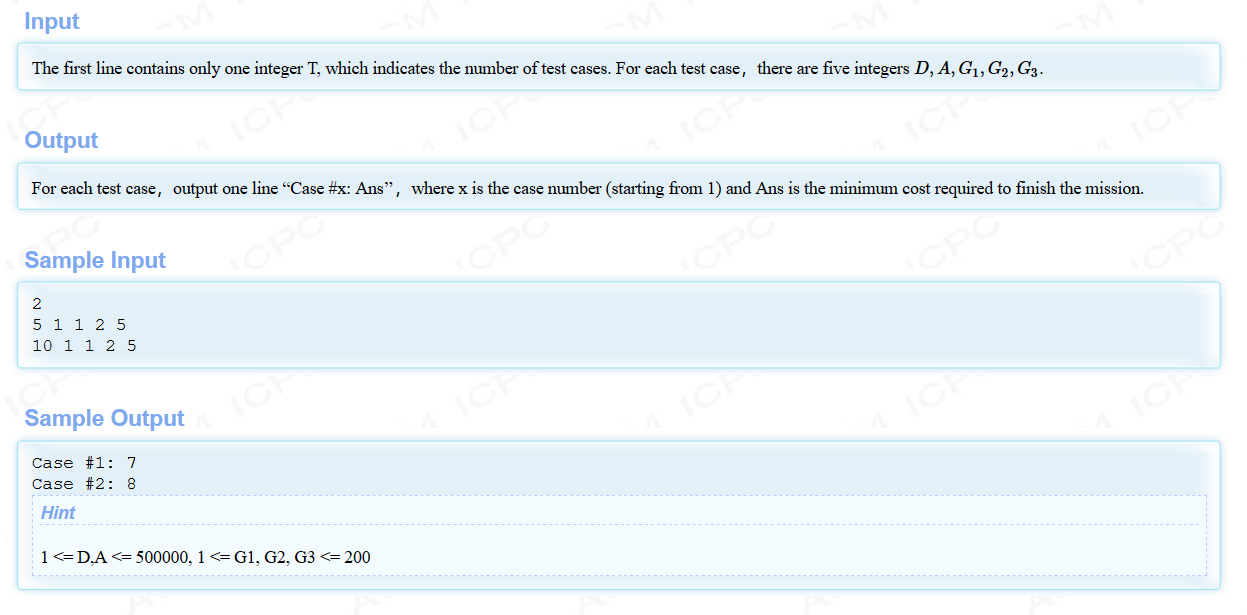
题意：
你要穿过长度为d的区域，你每秒会被攻击掉A的血量，当你某一秒的血量小于0时你将死亡（刚好等于0时不会死亡）。你初始时的血量、速度、血量恢复值都为0，但是你可以随时花费G1的钱来增加1单位的血，G2的钱来增加1单位的速度（不能大于d），G3的钱来增加G3的恢复速度，问你能通过这片区域的最小花费。
思路：
这就是一个贪心模拟，不是很懂这题为什么给18s的时限……你肯定是在出发时将三个的属性提高到一定的值再出发时最优，然后你通过这片区域可以有两种方法，一种是你的速度足够快，在到达终点时血量仍然大于等于0，另一种方法是你每秒减少的血量恰好等于你每秒恢复的血量值。我们可以进行枚举速度从1到d，然后将这两种方法进行比较取最小值。（ps.这题貌似卡中间过程的精度，很烦。）
代码实现如下：
#include <set>
#include <map>
#include <queue>
#include <stack>
#include <cmath>
#include <bitset>
#include <cstdio>
#include <string>
#include <vector>
#include <cstdlib>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std; typedef long long LL;
typedef pair<LL, LL> pLL;
typedef pair<LL, int> pli;
typedef pair<int, LL> pil;;
typedef pair<int, int> pii;
typedef unsigned long long uLL; #define lson i<<1
#define rson i<<1|1
#define lowbit(x) x&(-x)
#define bug printf("*********\n");
#define debug(x) cout<<"["<<x<<"]" <<endl;
#define FIN freopen("D://code//in.txt", "r", stdin);
#define IO ios::sync_with_stdio(false),cin.tie(0); const double eps = 1e-;
const int mod = 1e9 + ;
const int maxn = + ;
const double pi = acos(-);
const int inf = 0x3f3f3f3f;
const LL INF = 0x3f3f3f3f3f3f3f3f; int t, d, a, g1, g2, g3; int main() {
//FIN;
int icase = ;
scanf("%d", &t);
while(t--) {
scanf("%d%d%d%d%d", &d, &a, &g1, &g2, &g3);
LL ans = INF;
for(int i = ; i <= d; i++) {
double pp = 1.0 * d / i;
LL cnt1 = 1LL*ceil(pp * a)*g1;
LL cnt2 = 1LL * a * (g1 + g3);
LL tmp = cnt1 + 1LL * i * g2;
ans = min(tmp, ans);
ans = min(ans, cnt2 + 1LL * i * g2);
}
printf("Case #%d: %lld\n", ++icase, ans);
}
return ;
}
2016CCPC东北地区大学生程序设计竞赛 （2018年8月22日组队训练赛）的更多相关文章
- HDU 5925 Coconuts 【离散化+BFS】 （2016CCPC东北地区大学生程序设计竞赛）
Coconuts Time Limit: 9000/4500 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others)Total Su ...
- HDU 5929 Basic Data Structure 【模拟】 （2016CCPC东北地区大学生程序设计竞赛）
Basic Data Structure Time Limit: 7000/3500 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Oth ...
- HDU 5926 Mr. Frog's Game 【模拟】 （2016CCPC东北地区大学生程序设计竞赛）
Mr. Frog's Game Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others)T ...
- HDU 5924 Mr. Frog’s Problem 【模拟】 (2016CCPC东北地区大学生程序设计竞赛)
Mr. Frog's Problem Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Other ...
- HDU 5922 Minimum’s Revenge 【模拟】 (2016CCPC东北地区大学生程序设计竞赛)
Minimum's Revenge Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others ...
- HDU 5927 Auxiliary Set 【DFS+树】(2016CCPC东北地区大学生程序设计竞赛)
Auxiliary Set Time Limit: 9000/4500 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others)Tot ...
- 2016CCPC东北地区大学生程序设计竞赛 1008 HDU5929
链接http://acm.hdu.edu.cn/showproblem.php?pid=5929 题意:给你一种数据结构以及操作,和一种位运算,最后询问:从'栈'顶到低的运算顺序结果是多少 解法:根据 ...
- 2016CCPC东北地区大学生程序设计竞赛 1005 HDU5926
链接http://acm.hdu.edu.cn/showproblem.php?pid=5926 题意:给我们一个矩阵,问你根据连连看的玩法可以消去其中的元素 解法:连连看怎么玩,就怎么写,别忘记边界 ...
- 2016CCPC东北地区大学生程序设计竞赛 1003 HDU5924
链接http://acm.hdu.edu.cn/showproblem.php?pid=5924 题意:根据公式求C,D 解法:打表找规律 #include <bits/stdc++.h> ...
随机推荐
- Scrum 项目 5.0
5.0--------------------------------------------------- 1.团队成员完成自己认领的任务. 2.燃尽图:理解.设计并画出本次Sprint的燃尽图的理 ...
- 【acm】杀人游戏（hdu2211）
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=2211 杀人游戏 Time Limit: 3000/1000 MS (Java/Others) M ...
- 微信获取 openid 静默及非静默
<?php /* 需要的微信公众号配置信息 APPID : 绑定支付的APPID APPSECRET : 公众帐号secert */ class Index { // 配置账号信息 privat ...
- php奇葩错误：htmlspecialchars处理中文丢失
$value = "中文中文"; $res = htmlspecialchars($value); 经过这个函数处理之后,$res就直接变成了空的字符串. 奇葩错误啊!后来发现要这 ...
- Spring Security 入门详解
序:本文主要参考 spring实战 对里面的知识做一个梳理 1.Spring Security介绍 Spring Security是基于spring的应用程序提供声明式安全保护的安全性框架,它提供了完 ...
- bzoj4569-萌萌哒
题目 有一个长度为\(n\)的十进制数,用\(s\)表示.有\(m\)个限制条件,每个条件形如:\((l_1,r_1,l_2,r_2)\),表示\(s[l_1:r_1]=s[l_2:r_2]\). 现 ...
- elsarticle模板 去掉摘要前后的两条横线
参考:http://www.newsmth.net/nForum/#!article/TeX/316697?au=ericfire 如图:使用elsarticle模板修改PDF格式,去掉摘要前后的横线 ...
- C++解析-外传篇(3)：动态内存申请的结果
0.目录 1.动态内存申请一定成功吗? 2.new_handler() 函数 3.小结 1.动态内存申请一定成功吗? 问题: 动态内存申请一定成功吗? 常见的动态内存分配代码: C代码: C++代码: ...
- 【HDU4652】Dice（数学期望，动态规划）
[HDU4652]Dice(数学期望,动态规划) 题面 Vjudge 有一个\(m\)面骰子 询问,连续出现\(n\)个相同的时候停止的期望 连续出现\(n\)个不同的时候停止的期望 题解 考虑两种分 ...
- JAVA本地TXT文件解决中文乱码问题
import java.io.*; public class ReadFile { public static void main(String[] args) { try { File file = ...