Python实现二叉树的遍历

二叉树是有限个元素的集合，该集合或者为空、或者有一个称为根节点（root）的元素及两个互不相交的、分别被称为左子树和右子树的二叉树组成。

• 二叉树的每个结点至多只有二棵子树(不存在度大于2的结点)，二叉树的子树有左右之分，次序不能颠倒。
• 二叉树的第i层至多有2^{i-1}个结点
• 深度为k的二叉树至多有2^k-1个结点；
• 对任何一棵二叉树T，如果其终端结点数为N0，度为2的结点数为N2，则N0=N2+1

首先构建二叉树：

 class Node:
     def __init__(self,value=None,left=None,right=None):
         self.value=value
         self.left=left    #左子树
         self.right=right  #右子树

下面给出二叉树的前序遍历／中序遍历／后序遍历

 def preTraverse(root):
     '''
     前序遍历
     '''
     if root==None:
         return
     print(root.value)
     preTraverse(root.left)
     preTraverse(root.right)  

 def midTraverse(root):
     '''
     中序遍历
     '''
     if root==None:
         return
     midTraverse(root.left)
     print(root.value)
     midTraverse(root.right)  

 def afterTraverse(root):
     '''
     后序遍历
     '''
     if root==None:
         return
     afterTraverse(root.left)
     afterTraverse(root.right)
     print(root.value)  

下面给出一个例子，验证一下程序

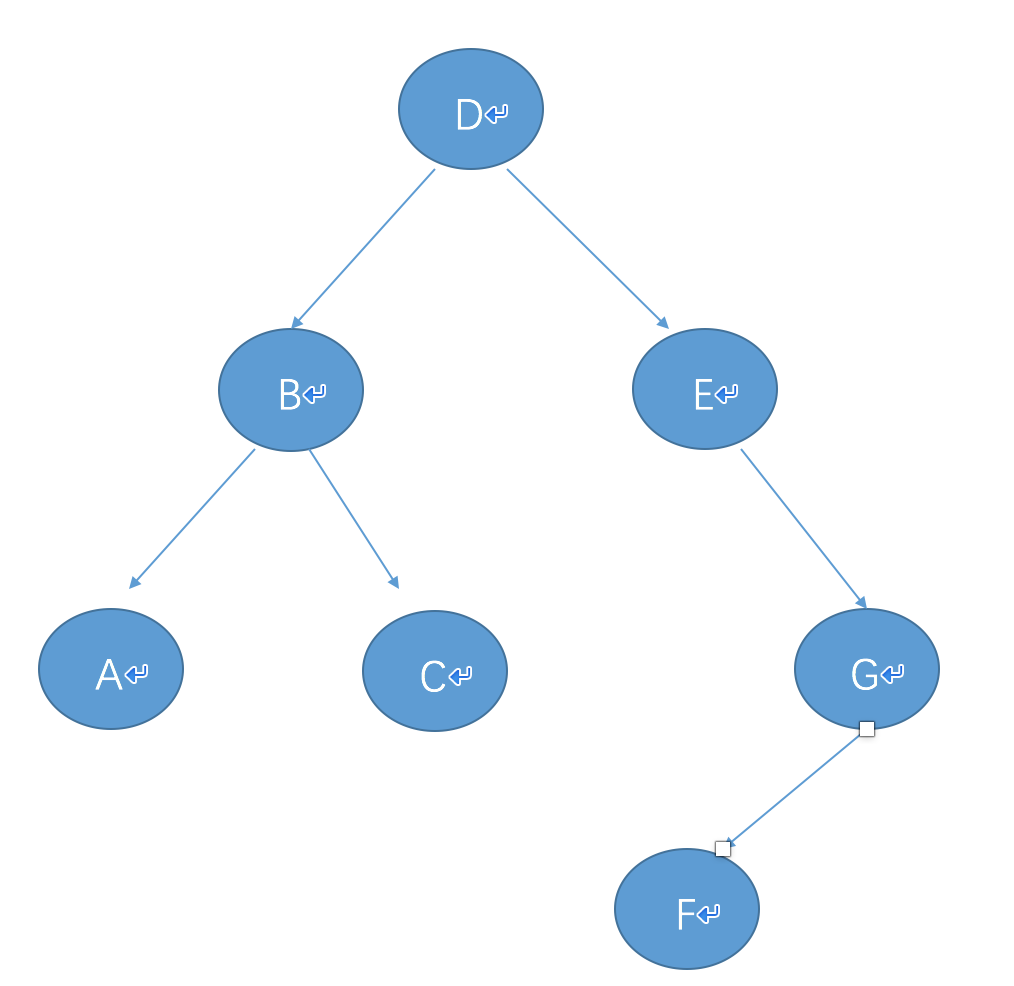
 if __name__=='__main__':
     root=Node('D',Node('B',Node('A'),Node('C')),Node('E',right=Node('G',Node('F'))))
     print('前序遍历：')
     preTraverse(root)
     print('\n')
     print('中序遍历：')
     midTraverse(root)
     print('\n')
     print('后序遍历：')
     afterTraverse(root)
     print('\n')

输出的结果为

前序遍历：
D
B
A
C
E
G
F

中序遍历：
A
B
C
D
E
F
G

后序遍历：
A
C
B
F
G
E
D

那么，如果我们已知二叉树的前序遍历和中序遍历，求这棵二叉树的后序遍历

 preList = list('')
 midList = list('')
 afterList = []

 def findTree(preList, midList, afterList):
     if len(preList) == 0:
         return
     if len(preList) == 1:
         afterList.append(preList[0])
         return
     root = preList[0]
     n = midList.index(root)
     findTree(preList[1:n + 1], midList[:n], afterList)
     findTree(preList[n + 1:], midList[n + 1:], afterList)
     afterList.append(root)

结果为：

['', '', '', '', '', '', '', '']

 如果以上面的前序：DBACEGF和中序：ABCDEFG，得到的结果为：
 ['A', 'C', 'B', 'F', 'G', 'E', 'D']