bzoj4199: [Noi2015]品酒大会（后缀数组）

题目描述

一年一度的“幻影阁夏日品酒大会”隆重开幕了。大会包含品尝和趣味挑战 两个环节，分别向优胜者颁发“首席品酒家”和“首席猎手”两个奖项，吸引了众多品酒师参加。

在大会的晚餐上，调酒师 Rainbow 调制了 n 杯鸡尾酒。这 n 杯鸡尾酒排成一行，其中第 n 杯酒 (1 ≤ i ≤ n) 被贴上了一个标签si，每个标签都是 26 个小写 英文字母之一。设 str(l, r)表示第 l 杯酒到第 r 杯酒的 r − l + 1 个标签顺次连接构成的字符串。若 str(p, po) = str(q, qo)，其中 1 ≤ p ≤ po ≤ n, 1 ≤ q ≤ qo ≤ n, p ≠ q, po − p + 1 = qo − q + 1 = r ，则称第 p 杯酒与第 q 杯酒是“ r 相似” 的。当然两杯“ r 相似”(r > 1)的酒同时也是“ 1 相似”、“ 2 相似”、……、“ (r − 1) 相似”的。特别地，对于任意的 1 ≤ p , q ≤ n ， p ≠ q ，第 p 杯酒和第 q 杯酒都 是“ 0 相似”的。

在品尝环节上，品酒师 Freda 轻松地评定了每一杯酒的美味度，凭借其专业的水准和经验成功夺取了“首席品酒家”的称号，其中第 i 杯酒 (1 ≤ i ≤ n) 的 美味度为 ai 。现在 Rainbow 公布了挑战环节的问题：本次大会调制的鸡尾酒有一个特点，如果把第 p 杯酒与第 q 杯酒调兑在一起，将得到一杯美味度为 ap*aq 的 酒。现在请各位品酒师分别对于 r = 0,1,2, ⋯ , n − 1 ，统计出有多少种方法可以 选出 2 杯“ r 相似”的酒，并回答选择 2 杯“ r 相似”的酒调兑可以得到的美味度的最大值。

输入输出格式

输入格式：

第 1 行包含 1 个正整数 n ，表示鸡尾酒的杯数。

第 2 行包含一个长度为 n 的字符串 S，其中第 i 个字符表示第 i 杯酒的标签。

第 3 行包含 n 个整数，相邻整数之间用单个空格隔开，其中第 i 个整数表示第 i 杯酒的美味度 ai 。

输出格式：

包括 n 行。第 i 行输出 2 个整数，中间用单个空格隔开。第 1 个整 数表示选出两杯“ (i − 1) 相似”的酒的方案数，第 2 个整数表示选出两杯 “ (i − 1) 相似”的酒调兑可以得到的最大美味度。若不存在两杯“ (i − 1) 相似” 的酒，这两个数均为 0 。

输入输出样例

输入样例#1： 复制

10
ponoiiipoi
2 1 4 7 4 8 3 6 4 7

输出样例#1： 复制

45 56
10 56
3 32
0 0
0 0
0 0
0 0
0 0
0 0
0 0

输入样例#2： 复制

12
abaabaabaaba
1 -2 3 -4 5 -6 7 -8 9 -10 11 -12

输出样例#2： 复制

66 120
34 120
15 55
12 40
9 27
7 16
5 7
3 -4
2 -4
1 -4
0 0
0 0

说明

【样例说明 1】

用二元组 (p, q) 表示第 p 杯酒与第 q 杯酒。

0 相似：所有 45 对二元组都是 0 相似的，美味度最大的是 8 × 7 = 56 。

1 相似： (1,8) (2,4) (2,9) (4,9) (5,6) (5,7) (5,10) (6,7) (6,10) (7,10) ，最大的 8 × 7 = 56 。

2 相似： (1,8) (4,9) (5,6) ，最大的 4 × 8 = 32 。

没有 3,4,5, ⋯ ,9 相似的两杯酒，故均输出 0 。

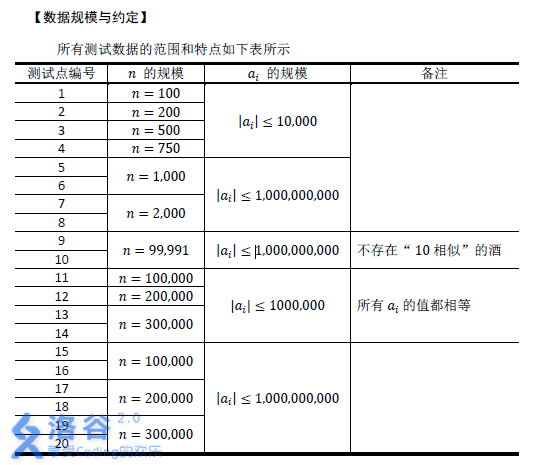
【时限1s，内存512M】

 题解

　　我果然还是太弱……学了这么久后缀系列竟然连这么一道裸题都看不出来……

　　考虑一下，如果两杯酒是$r$相似的，那么他们肯定也是$[0,r-1]$相似的，所以大的可以对小的产生贡献

　　于是就跑一遍SA，求出height数组，然后把height从大到小排个序，每次取出height一样的合并就是了

　　考虑怎么合并，可以用并查集实现，两个集合合并之后方案数$sum[x]+=size[x]*size[y]$（因为两个集合中所有元素都是$r$相似的，而且集合中的两两匹配已经考虑过了，所以只要加上两个集合之间互相匹配的就是了），然后再用$mx[x]*mx[y]$和$mn[x]*mn[y]$更新一下$ans[x]$就可以了（记录最小是因为负负得正）

　　据说这题还有SAM的做法，因为做的时候只要考虑两串的最长相似，然后答案做一下前缀和。而一对串的最长相似就是两个后缀的lcp，直接把原串翻转SAM转后缀树，然后dfs一遍即可（明明这么裸我居然没有看出来啊岂可修）

　　

 //minamoto
 #include<cstdio>
 #include<algorithm>
 #include<iostream>
 #include<cstring>
 #define ll long long
 using namespace std;
 #define getc() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
 char buf[<<],*p1=buf,*p2=buf;
 template<class T>inline bool cmax(T&a,const T&b){return a<b?a=b,:;}
 template<class T>inline bool cmin(T&a,const T&b){return a>b?a=b,:;}
 inline int read(){
     #define num ch-'0'
     char ch;bool flag=;int res;
     while(!isdigit(ch=getc()))
     (ch=='-')&&(flag=true);
     for(res=num;isdigit(ch=getc());res=res*+num);
     (flag)&&(res=-res);
     #undef num
     return res;
 }
 char sr[<<],z[];int C=-,Z;
 inline void Ot(){fwrite(sr,,C+,stdout),C=-;}
 inline void print(ll x,char ch){
     if(C><<)Ot();if(x<)sr[++C]=,x=-x;
     while(z[++Z]=x%+,x/=);
     while(sr[++C]=z[Z],--Z);sr[++C]=ch;
 }
 const int N=;
 int s[N],y[N],x[N],c[N],sa[N],rk[N],h[N];
 int n,m;
 int fa[N],sz[N];ll ans[N],sum[N],mx[N],mn[N],val[N];
 struct node{
     int h,x,y;
     node(){}
     node(int h,int x,int y):h(h),x(x),y(y){}
     inline bool operator <(const node &b)const
     {return h>b.h;}
 }g[N];
 int ff(int x){return fa[x]==x?x:fa[x]=ff(fa[x]);}
 void unite(int x,int y){
     fa[y]=x,sz[x]+=sz[y];
     cmax(mx[x],mx[y]),cmin(mn[x],mn[y]);
 }
 void get_sa(){
     m=;
     for(int i=;i<=n;i++) ++c[x[i]=s[i]];
     for(int i=;i<=m;i++) c[i]+=c[i-];
     for(int i=n;i>=;i--) sa[c[x[i]]--]=i;
     for(int k=;k<=n;k<<=){
         int num=;
         for(int i=n-k+;i<=n;i++) y[++num]=i;
         for(int i=;i<=n;i++) if(sa[i]>k) y[++num]=sa[i]-k;
         for(int i=;i<=m;i++) c[i]=;
         for(int i=;i<=n;i++) ++c[x[i]];
         for(int i=;i<=m;i++) c[i]+=c[i-];
         for(int i=n;i>=;i--) sa[c[x[y[i]]]--]=y[i],y[i]=;
         swap(x,y);
         x[sa[]]=;
         num=;
         for(int i=;i<=n;i++)
         x[sa[i]]=(y[sa[i]]==y[sa[i-]]&&y[sa[i]+k]==y[sa[i-]+k])?num:++num;
         if(num==n) break;
         m=num;
     }
 }
 void get_h(){
     int k=;
     for(int i=;i<=n;i++) rk[sa[i]]=i;
     for(int i=;i<=n;i++){
         if(rk[i]==) continue;
         if(k) k--;
         int j=sa[rk[i]-];
         while(j+k<=n&&i+k<=n&&s[i+k]==s[j+k]) k++;
         h[rk[i]]=k;
     }
 }
 int main(){
     n=read();
     for(int i=;i<=n;++i) s[i]=getc()-'a'+;
     for(int i=;i<=n;++i) val[i]=read();
     get_sa(),get_h();
     for(int i=;i<=n;++i){
         fa[i]=i,sz[i]=;
         mx[rk[i]]=mn[rk[i]]=val[i];
     }
     for(int i=;i<=n;++i) g[i-]=node(h[i],i,i-);
     sort(g+,g+n);
     memset(sum,,sizeof(sum));
     for(int i=g[].h,j=;i>=;--i){
         ans[i]=ans[i+],sum[i]=sum[i+];
         for(;j<n&&g[j].h==i;++j){
             int x=ff(g[j].x),y=ff(g[j].y);
             cmax(sum[i],mn[x]*mn[y]);
             cmax(sum[i],mx[x]*mx[y]);
             ans[i]+=1ll*sz[x]*sz[y];
             unite(x,y);
         }
     }
     for(int i=;i<n;++i){
         print(ans[i],' ');
         print(ans[i]==?:sum[i],'\n');
     }
     Ot();
     return ;
 }