Codeforces 691E Xor-sequences（矩阵快速幂）

You are given n integers a1,  a2,  ...,  an.

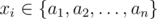A sequence of integers x1,  x2,  ...,  xk is called a "xor-sequence" if for every 1  ≤  i  ≤  k - 1 the number of ones in the binary representation of the number xi  xi  +  1's is a multiple of 3 and  for all 1 ≤ i ≤ k. The symbol  is used for the binary exclusive or operation.

How many "xor-sequences" of length k exist? Output the answer modulo 109 + 7.

Note if a = [1, 1] and k = 1 then the answer is 2, because you should consider the ones from a as different.

Input

The first line contains two integers n and k (1 ≤ n ≤ 100, 1 ≤ k ≤ 1018) — the number of given integers and the length of the "xor-sequences".

The second line contains n integers ai (0 ≤ ai ≤ 1018).

Output

Print the only integer c — the number of "xor-sequences" of length k modulo 109 + 7.

Examples

input

5 2
15 1 2 4 8

output

13

input

5 1
15 1 2 4 8

output

5

题意：给出n个数，让你取出k个构成一个新串，使这些串中每相邻两个数异或起来得到的数二进制表达下一的个数是三的倍数，求这些串的个数

题解：显然可以暴力预处理出构成长度为2的方法，然后用矩阵快速幂跑一下就可以了

代码如下：

#include<map>
#include<set>
#include<queue>
#include<cmath>
#include<cstdio>
#include<string>
#include<vector>
#include<cstring>
#include<iostream>
#include<algorithm>
#define mod 1000000007
#define int long long
using namespace std;

struct matrix
{
    int  m[][];
    void init()
    {
        for(int i=;i<=;i++)
        {
            m[i][i]=;
        }
    }
    void clr()
    {
        memset(m,,sizeof(m));
    }
};

int n,m[];
int k;

matrix mul(matrix a,matrix b)
{
    matrix ans;
    ans.clr();
    for(int i=;i<=n;i++)
    {
        for(int j=;j<=n;j++)
        {
            for(int k=;k<=n;k++)
            {
                ans.m[i][j]+=a.m[i][k]*b.m[k][j];
                ans.m[i][j]%=mod;
            }
        }
    }
    return ans;
}

matrix kasumi(matrix a,int  b)
{
    matrix ans;
    ans.clr();
    ans.init();
    while(b)
    {
        if(b&)
        {
            ans=mul(ans,a);
        }
        a=mul(a,a);
        b>>=;
    }
    return ans;
}

signed main()
{
    scanf("%lld%lld",&n,&k);
    for(int i=;i<=n;i++)
    {
        scanf("%lld",&m[i]);
    }
    matrix x;
    x.clr();
    for(int i=;i<=n;i++)
    {
        for(int j=;j<=n;j++)
        {
            if(__builtin_popcountll(m[i]^m[j])%==)
            {
                x.m[i][j]=;
            }
        }
    }
    x=kasumi(x,k-);
    int ans=0ll;
    for(int i=;i<=n;i++)
    {
        for(int j=;j<=n;j++)
        {
            ans+=x.m[i][j];
            ans%=mod;
        }
    }
    printf("%lld\n",ans);
}